Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 173516 by SANOGO last updated on 12/Jul/22

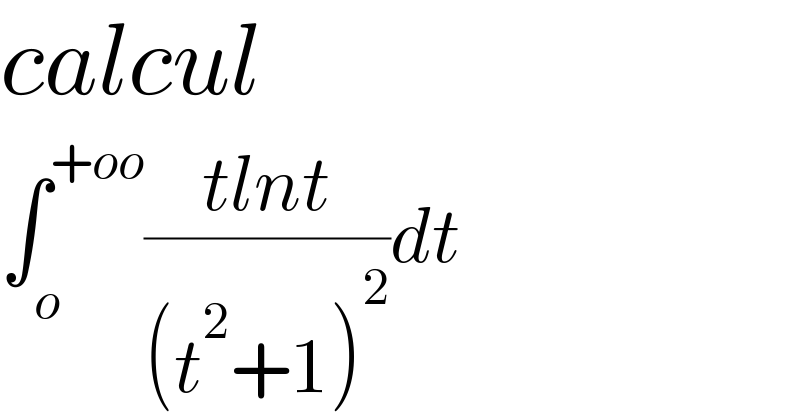
calcul ∫_o ^(+oo) ((tlnt)/((t^2 +1)^2 ))dt

$${calcul} \\ $$$$\int_{{o}} ^{+{oo}} \frac{{tlnt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$

Answered by aleks041103 last updated on 12/Jul/22

∫((t lnt)/((t^2 +1)^2 ))dt=−(1/2)∫^ lnt d((1/(1+t^2 )))= =−((ln(t))/(2(1+t^2 )))+(1/2)∫(dt/(t(1+t^2 )))= =−((ln(t))/(2(1+t^2 )))+(1/4)∫((2tdt)/(t^2 (1+t^2 )))= =−((ln(t))/(2(1+t^2 )))+(1/4)∫(du/(u(1+u)))= =−((ln(t))/(2(1+t^2 )))+(1/4)∫((1/u)−(1/(u+1)))du= =−((ln(t))/(2(1+t^2 )))+(1/4)ln∣(u/(u+1))∣ ⇒∫ ((t ln(t) dt)/((1+t^2 )^2 ))=(1/4)ln((t^2 /(1+t^2 )))−((ln(t))/(2(1+t^2 ))) easy to see that ∫_0 ^∞ ((t ln(t) dt)/((1+t^2 )^2 ))=[(1/4)ln((t^2 /(1+t^2 )))−((ln(t))/(2(1+t^2 )))]_0 ^∞ =0

$$\int\frac{{t}\:{lnt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dt}=−\frac{\mathrm{1}}{\mathrm{2}}\int^{\:} {lnt}\:{d}\left(\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)= \\ $$$$=−\frac{{ln}\left({t}\right)}{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}= \\ $$$$=−\frac{{ln}\left({t}\right)}{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{2}{tdt}}{{t}^{\mathrm{2}} \left(\mathrm{1}+{t}^{\mathrm{2}} \right)}= \\ $$$$=−\frac{{ln}\left({t}\right)}{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{du}}{{u}\left(\mathrm{1}+{u}\right)}= \\ $$$$=−\frac{{ln}\left({t}\right)}{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}+\frac{\mathrm{1}}{\mathrm{4}}\int\left(\frac{\mathrm{1}}{{u}}−\frac{\mathrm{1}}{{u}+\mathrm{1}}\right){du}= \\ $$$$=−\frac{{ln}\left({t}\right)}{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}+\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid\frac{{u}}{{u}+\mathrm{1}}\mid \\ $$$$\Rightarrow\int\:\frac{{t}\:{ln}\left({t}\right)\:{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)−\frac{{ln}\left({t}\right)}{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$${easy}\:{to}\:{see}\:{that} \\ $$$$\:\int_{\mathrm{0}} ^{\infty} \:\frac{{t}\:{ln}\left({t}\right)\:{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }=\left[\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)−\frac{{ln}\left({t}\right)}{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}\right]_{\mathrm{0}} ^{\infty} =\mathrm{0} \\ $$

Commented by Tawa11 last updated on 13/Jul/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Answered by aleks041103 last updated on 12/Jul/22

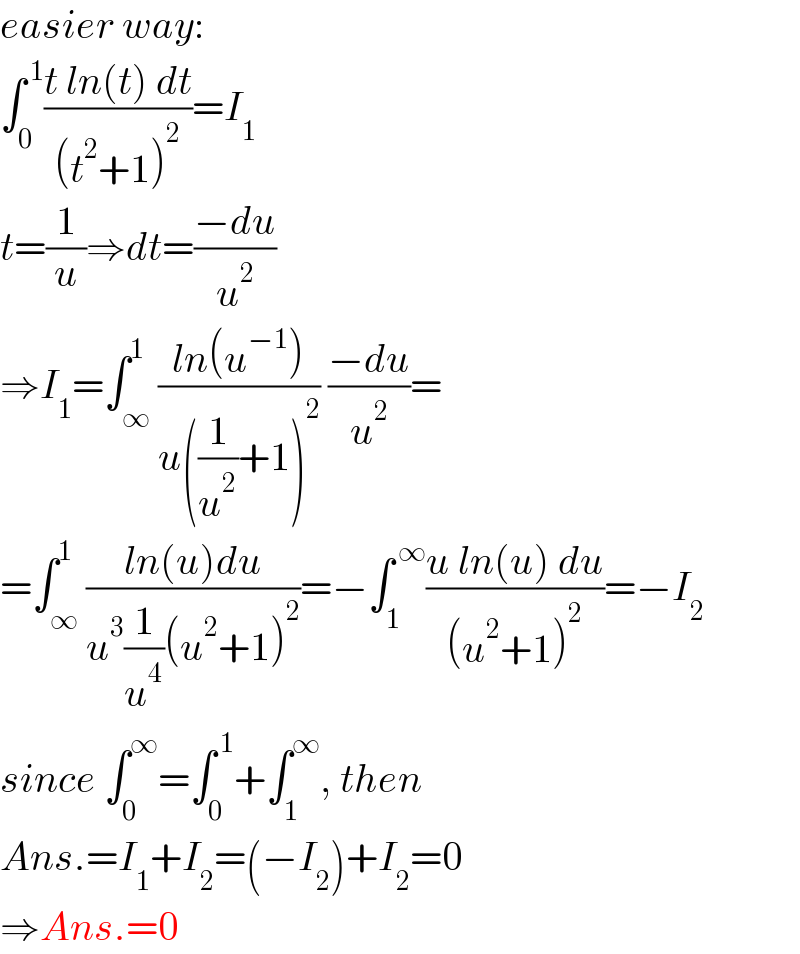
easier way: ∫_0 ^( 1) ((t ln(t) dt)/((t^2 +1)^2 ))=I_1 t=(1/u)⇒dt=((−du)/u^2 ) ⇒I_1 =∫_∞ ^1 ((ln(u^(−1) ))/(u((1/u^2 )+1)^2 )) ((−du)/u^2 )= =∫_∞ ^1 ((ln(u)du)/(u^3 (1/u^4 )(u^2 +1)^2 ))=−∫_1 ^( ∞) ((u ln(u) du)/((u^2 +1)^2 ))=−I_2 since ∫_0 ^∞ =∫_0 ^( 1) +∫_1 ^∞ , then Ans.=I_1 +I_2 =(−I_2 )+I_2 =0 ⇒Ans.=0

$${easier}\:{way}: \\ $$$$\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{t}\:{ln}\left({t}\right)\:{dt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }={I}_{\mathrm{1}} \\ $$$${t}=\frac{\mathrm{1}}{{u}}\Rightarrow{dt}=\frac{−{du}}{{u}^{\mathrm{2}} } \\ $$$$\Rightarrow{I}_{\mathrm{1}} =\int_{\infty} ^{\mathrm{1}} \frac{{ln}\left({u}^{−\mathrm{1}} \right)}{{u}\left(\frac{\mathrm{1}}{{u}^{\mathrm{2}} }+\mathrm{1}\right)^{\mathrm{2}} }\:\frac{−{du}}{{u}^{\mathrm{2}} }= \\ $$$$=\int_{\infty} ^{\mathrm{1}} \frac{{ln}\left({u}\right){du}}{{u}^{\mathrm{3}} \frac{\mathrm{1}}{{u}^{\mathrm{4}} }\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }=−\int_{\mathrm{1}} ^{\:\infty} \frac{{u}\:{ln}\left({u}\right)\:{du}}{\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }=−{I}_{\mathrm{2}} \\ $$$${since}\:\int_{\mathrm{0}} ^{\infty} =\int_{\mathrm{0}} ^{\:\mathrm{1}} +\int_{\mathrm{1}} ^{\infty} ,\:{then} \\ $$$${Ans}.={I}_{\mathrm{1}} +{I}_{\mathrm{2}} =\left(−{I}_{\mathrm{2}} \right)+{I}_{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{Ans}.=\mathrm{0} \\ $$

Commented by Tawa11 last updated on 13/Jul/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Answered by mnjuly1970 last updated on 13/Jul/22

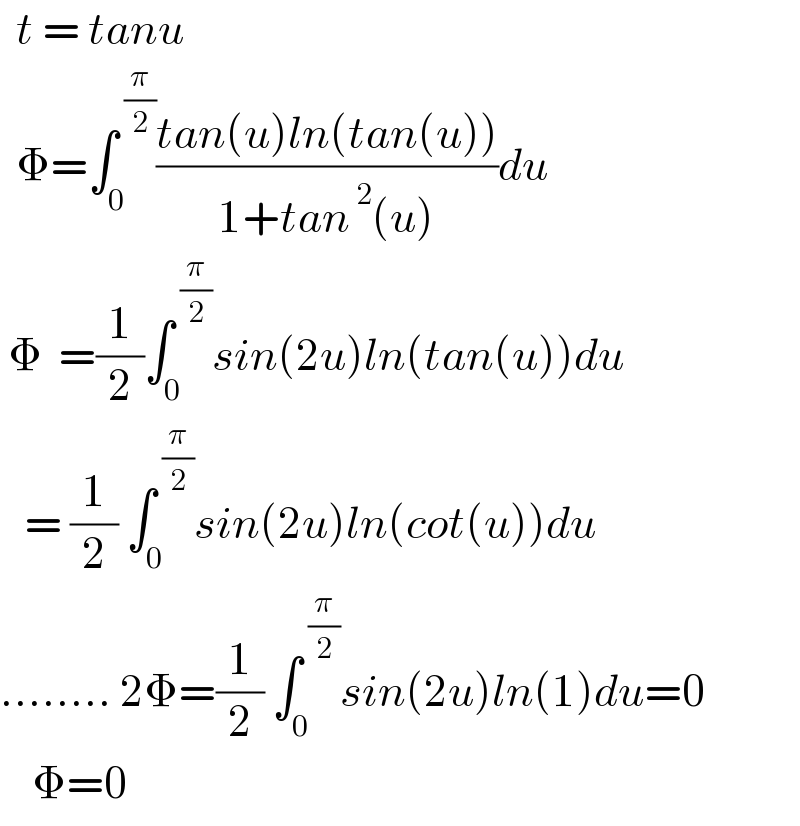
t = tanu Φ=∫_0 ^( (π/2)) ((tan(u)ln(tan(u)))/(1+tan^( 2) (u)))du Φ =(1/2)∫_(0 ) ^( (π/2)) sin(2u)ln(tan(u))du = (1/2) ∫_0 ^( (π/2)) sin(2u)ln(cot(u))du ........ 2Φ=(1/2) ∫_0 ^( (π/2)) sin(2u)ln(1)du=0 Φ=0

$$\:\:{t}\:=\:{tanu} \\ $$$$\:\:\Phi=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{{tan}\left({u}\right){ln}\left({tan}\left({u}\right)\right)}{\mathrm{1}+{tan}^{\:\mathrm{2}} \left({u}\right)}{du} \\ $$$$\:\Phi\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}\:} ^{\:\frac{\pi}{\mathrm{2}}} {sin}\left(\mathrm{2}{u}\right){ln}\left({tan}\left({u}\right)\right){du} \\ $$$$\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {sin}\left(\mathrm{2}{u}\right){ln}\left({cot}\left({u}\right)\right){du} \\ $$$$........\:\mathrm{2}\Phi=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {sin}\left(\mathrm{2}{u}\right){ln}\left(\mathrm{1}\right){du}=\mathrm{0} \\ $$$$\:\:\:\:\Phi=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com