
Question Number 173566 by Khalmohmmad last updated on 13/Jul/22

Answered by MJS_new last updated on 13/Jul/22

$${x}=\mathrm{0}\vee{x}=−\infty \\ $$
Answered by mr W last updated on 13/Jul/22
![obvious: x=0 or using Lambert W−function: ((3/2))^x =1−(x/2) ((9/4))((9/4))^((x/2)−1) =1−(x/2) (9/4)ln (9/4)=[(1−(x/2))ln (9/4)]e^((1−(x/2))ln (9/4)) W((9/4)ln (9/4))=(1−(x/2))ln (9/4) x=2[1−(1/(ln (9/4)))W((9/4)ln (9/4))] ⇒x=2−((W((9/2)ln (3/2)))/(ln (3/2)))=0](Q173568.png)
$${obvious}:\:{x}=\mathrm{0} \\ $$$${or}\:{using}\:{Lambert}\:{W}−{function}: \\ $$$$\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{{x}} =\mathrm{1}−\frac{{x}}{\mathrm{2}} \\ $$$$\left(\frac{\mathrm{9}}{\mathrm{4}}\right)\left(\frac{\mathrm{9}}{\mathrm{4}}\right)^{\frac{{x}}{\mathrm{2}}−\mathrm{1}} =\mathrm{1}−\frac{{x}}{\mathrm{2}} \\ $$$$\frac{\mathrm{9}}{\mathrm{4}}\mathrm{ln}\:\frac{\mathrm{9}}{\mathrm{4}}=\left[\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)\mathrm{ln}\:\frac{\mathrm{9}}{\mathrm{4}}\right]{e}^{\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)\mathrm{ln}\:\frac{\mathrm{9}}{\mathrm{4}}} \\ $$$${W}\left(\frac{\mathrm{9}}{\mathrm{4}}\mathrm{ln}\:\frac{\mathrm{9}}{\mathrm{4}}\right)=\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)\mathrm{ln}\:\frac{\mathrm{9}}{\mathrm{4}} \\ $$$${x}=\mathrm{2}\left[\mathrm{1}−\frac{\mathrm{1}}{\mathrm{ln}\:\frac{\mathrm{9}}{\mathrm{4}}}{W}\left(\frac{\mathrm{9}}{\mathrm{4}}\mathrm{ln}\:\frac{\mathrm{9}}{\mathrm{4}}\right)\right] \\ $$$$\Rightarrow{x}=\mathrm{2}−\frac{{W}\left(\frac{\mathrm{9}}{\mathrm{2}}\mathrm{ln}\:\frac{\mathrm{3}}{\mathrm{2}}\right)}{\mathrm{ln}\:\frac{\mathrm{3}}{\mathrm{2}}}=\mathrm{0} \\ $$
Commented by Tawa11 last updated on 13/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by a.lgnaoui last updated on 14/Jul/22
![2^x −3^x =(x/2)2^x (2^x −3^x )^2 =(x^2 /4)2^(2x ) ⇒2^(2x) +3^(2x) −2×2^x ×3^x =((x/2)2^x )^2 (2^x −3^x )^2 −((x/2)2^x )^2 =0 ⇒ [2^x −3^x −2^x (x/2)][2^x −3^x +2^x (x/2)]=0 2^x −3^x =±2^x (x/2) 3^x =2^x (1−(x/2)) (1) 3^x =2^x (1+(x/2)) (2) (1)/(2)⇒ 1=((1−(x/2))/(1+(x/2))) ⇒x=0](Q173598.png)
$$\mathrm{2}^{\mathrm{x}} −\mathrm{3}^{\mathrm{x}} =\frac{\mathrm{x}}{\mathrm{2}}\mathrm{2}^{\mathrm{x}} \\ $$$$\left(\mathrm{2}^{\mathrm{x}} −\mathrm{3}^{\mathrm{x}} \right)^{\mathrm{2}} =\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}\mathrm{2}^{\mathrm{2x}\:} \:\:\Rightarrow\mathrm{2}^{\mathrm{2}{x}} +\mathrm{3}^{\mathrm{2}{x}} −\mathrm{2}×\mathrm{2}^{{x}} ×\mathrm{3}^{{x}} =\left(\frac{{x}}{\mathrm{2}}\mathrm{2}^{{x}} \right)^{\mathrm{2}} \\ $$$$\left(\mathrm{2}^{{x}} −\mathrm{3}^{{x}} \right)^{\mathrm{2}} −\left(\frac{{x}}{\mathrm{2}}\mathrm{2}^{{x}} \right)^{\mathrm{2}} =\mathrm{0}\:\Rightarrow \\ $$$$\left[\mathrm{2}^{{x}} −\mathrm{3}^{{x}} −\mathrm{2}^{{x}} \frac{{x}}{\mathrm{2}}\right]\left[\mathrm{2}^{{x}} −\mathrm{3}^{{x}} +\mathrm{2}^{{x}} \frac{{x}}{\mathrm{2}}\right]=\mathrm{0} \\ $$$$\:\:\mathrm{2}^{{x}} −\mathrm{3}^{{x}} =\pm\mathrm{2}^{{x}} \frac{{x}}{\mathrm{2}}\: \\ $$$$\mathrm{3}^{{x}} =\mathrm{2}^{{x}} \left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\mathrm{3}^{{x}} =\mathrm{2}^{{x}} \left(\mathrm{1}+\frac{{x}}{\mathrm{2}}\right)\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)/\left(\mathrm{2}\right)\Rightarrow\:\:\:\mathrm{1}=\frac{\mathrm{1}−\frac{{x}}{\mathrm{2}}}{\mathrm{1}+\frac{{x}}{\mathrm{2}}}\:\:\:\Rightarrow{x}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by a.lgnaoui last updated on 14/Jul/22

$${think}\:{Sir}. \\ $$
Commented by mr W last updated on 14/Jul/22
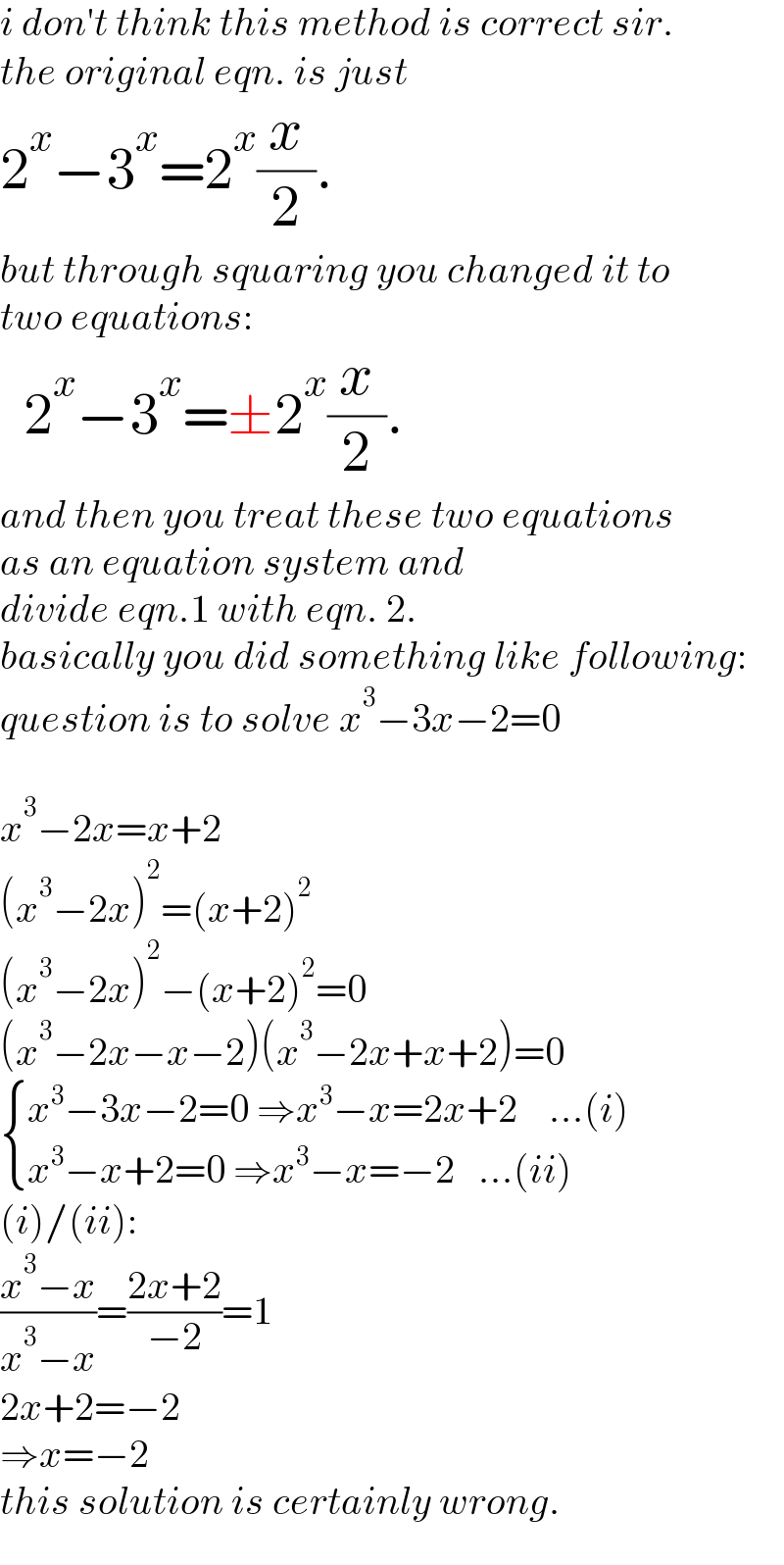
$${i}\:{don}'{t}\:{think}\:{this}\:{method}\:{is}\:{correct}\:{sir}. \\ $$$${the}\:{original}\:{eqn}.\:{is}\:{just} \\ $$$$\mathrm{2}^{{x}} −\mathrm{3}^{{x}} =\mathrm{2}^{{x}} \frac{{x}}{\mathrm{2}}. \\ $$$${but}\:{through}\:{squaring}\:{you}\:{changed}\:{it}\:{to} \\ $$$${two}\:{equations}: \\ $$$$\:\:\mathrm{2}^{{x}} −\mathrm{3}^{{x}} =\pm\mathrm{2}^{{x}} \frac{{x}}{\mathrm{2}}. \\ $$$${and}\:{then}\:{you}\:{treat}\:{these}\:{two}\:{equations}\: \\ $$$${as}\:{an}\:{equation}\:{system}\:{and} \\ $$$${divide}\:{eqn}.\mathrm{1}\:{with}\:{eqn}.\:\mathrm{2}.\: \\ $$$${basically}\:{you}\:{did}\:{something}\:{like}\:{following}: \\ $$$${question}\:{is}\:{to}\:{solve}\:{x}^{\mathrm{3}} −\mathrm{3}{x}−\mathrm{2}=\mathrm{0} \\ $$$$ \\ $$$${x}^{\mathrm{3}} −\mathrm{2}{x}={x}+\mathrm{2} \\ $$$$\left({x}^{\mathrm{3}} −\mathrm{2}{x}\right)^{\mathrm{2}} =\left({x}+\mathrm{2}\right)^{\mathrm{2}} \\ $$$$\left({x}^{\mathrm{3}} −\mathrm{2}{x}\right)^{\mathrm{2}} −\left({x}+\mathrm{2}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({x}^{\mathrm{3}} −\mathrm{2}{x}−{x}−\mathrm{2}\right)\left({x}^{\mathrm{3}} −\mathrm{2}{x}+{x}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\begin{cases}{{x}^{\mathrm{3}} −\mathrm{3}{x}−\mathrm{2}=\mathrm{0}\:\Rightarrow{x}^{\mathrm{3}} −{x}=\mathrm{2}{x}+\mathrm{2}\:\:\:\:...\left({i}\right)}\\{{x}^{\mathrm{3}} −{x}+\mathrm{2}=\mathrm{0}\:\Rightarrow{x}^{\mathrm{3}} −{x}=−\mathrm{2}\:\:\:...\left({ii}\right)}\end{cases} \\ $$$$\left({i}\right)/\left({ii}\right): \\ $$$$\frac{{x}^{\mathrm{3}} −{x}}{{x}^{\mathrm{3}} −{x}}=\frac{\mathrm{2}{x}+\mathrm{2}}{−\mathrm{2}}=\mathrm{1} \\ $$$$\mathrm{2}{x}+\mathrm{2}=−\mathrm{2} \\ $$$$\Rightarrow{x}=−\mathrm{2} \\ $$$${this}\:{solution}\:{is}\:{certainly}\:{wrong}. \\ $$
Commented by mr W last updated on 14/Jul/22

$${you}\:{are}\:{welcome}! \\ $$
