solve for x∈R ((5x−3)/(3x−5))=x^4


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 173574 by mr W last updated on 13/Jul/22

$s o l v e f o r x \in R$ $\frac{5 x - 3}{3 x - 5} = x^{4}$
Commented by kaivan.ahmadi last updated on 14/Jul/22
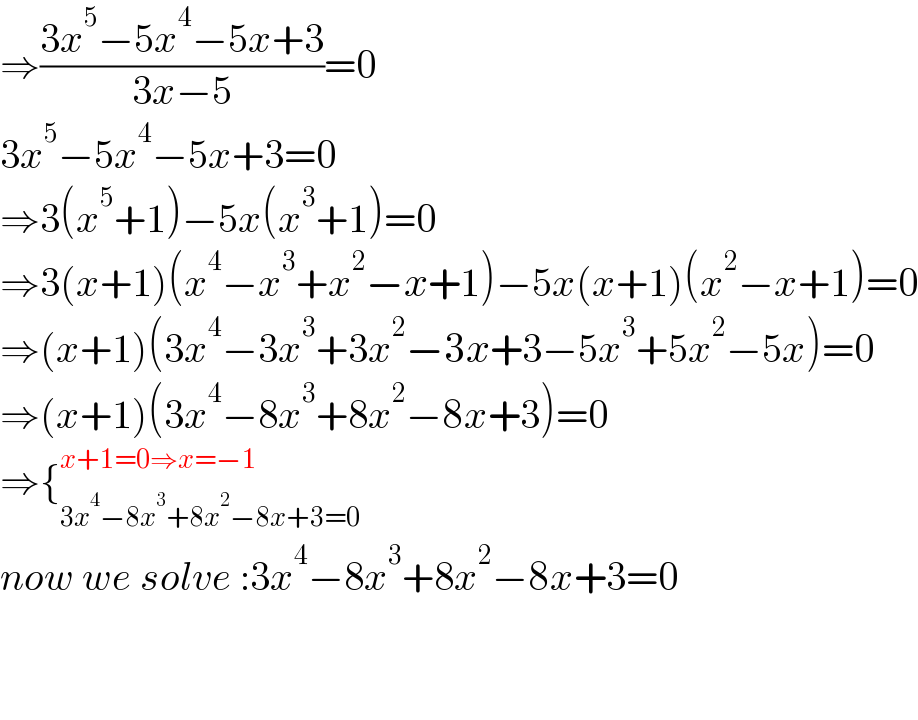
$⇒((3x^5 −5x^4 −5x+3)/(3x−5))=0 3x^5 −5x^4 −5x+3=0 ⇒3(x^5 +1)−5x(x^3 +1)=0 ⇒3(x+1)(x^4 −x^3 +x^2 −x+1)−5x(x+1)(x^2 −x+1)=0 ⇒(x+1)(3x^4 −3x^3 +3x^2 −3x+3−5x^3 +5x^2 −5x)=0 ⇒(x+1)(3x^4 −8x^3 +8x^2 −8x+3)=0 ⇒{_(3x^4 −8x^3 +8x^2 −8x+3=0) ^(x+1=0⇒x=−1) now we solve :3x^4 −8x^3 +8x^2 −8x+3=0$
$\Rightarrow \frac{3 x^{5} - 5 x^{4} - 5 x + 3}{3 x - 5} = 0$ $3 x^{5} - 5 x^{4} - 5 x + 3 = 0$ $\Rightarrow 3 (x^{5} + 1) - 5 x (x^{3} + 1) = 0$ $\Rightarrow 3 (x + 1) (x^{4} - x^{3} + x^{2} - x + 1) - 5 x (x + 1) (x^{2} - x + 1) = 0$ $\Rightarrow (x + 1) (3 x^{4} - 3 x^{3} + 3 x^{2} - 3 x + 3 - 5 x^{3} + 5 x^{2} - 5 x) = 0$ $\Rightarrow (x + 1) (3 x^{4} - 8 x^{3} + 8 x^{2} - 8 x + 3) = 0$ $\Rightarrow {_{3 x^{4} - 8 x^{3} + 8 x^{2} - 8 x + 3 = 0}^{x + 1 = 0 \Rightarrow x = - 1}$ $n o w w e s o l v e : 3 x^{4} - 8 x^{3} + 8 x^{2} - 8 x + 3 = 0$
Commented by aleks041103 last updated on 14/Jul/22

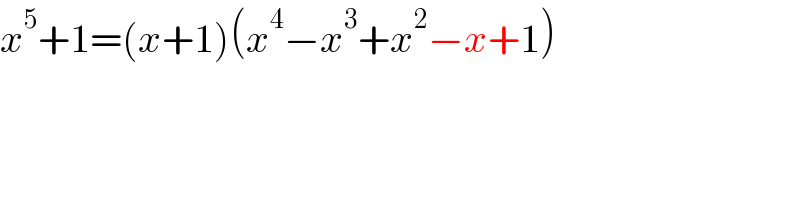
$x^{5} + 1 = (x + 1) (x^{4} - x^{3} + x^{2} - x + 1)$
Commented by kaivan.ahmadi last updated on 14/Jul/22

$t h a n k y o u$
Commented by mr W last updated on 14/Jul/22

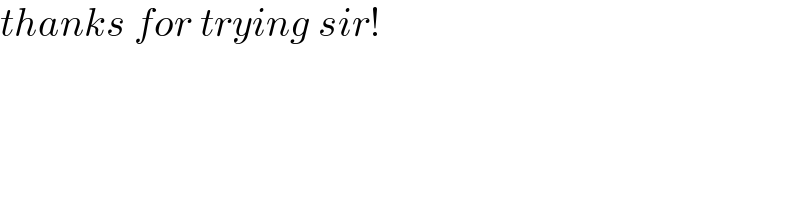
$t h a n k s f o r t r y i n g s i r!$
	Answered by CElcedricjunior last updated on 13/Jul/22

	${1}$
	Commented by mr W last updated on 14/Jul/22

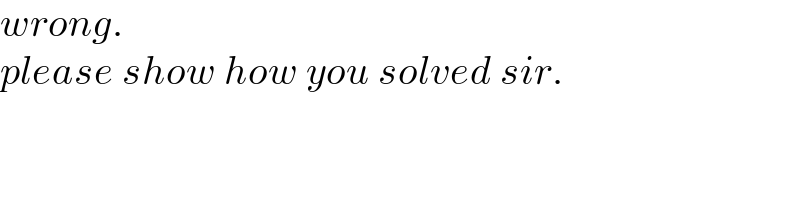
	$w r o n g .$ $p l e a s e s h o w h o w y o u s o l v e d s i r .$
	Answered by aleks041103 last updated on 14/Jul/22

	$5 x - 3 = 3 x^{5} - 5 x^{4}$ $3 x^{5} - 5 x^{4} - 5 x + 3 = 0$ $3 (x^{5} + 1) - 5 x (x^{3} + 1) = 0$ $3 (x + 1) (x^{4} - x^{3} + x^{2} - x + 1) - 5 x (x + 1) (x^{2} - x + 1) = 0$ $(x + 1) (3 x^{4} - 3 x^{3} + 3 x^{2} - 3 x + 3 - 5 x^{3} + 5 x^{2} - 5 x) = 0$ $(x + 1) (3 x^{4} - 8 x^{3} + 8 x^{2} - 8 x + 3) = 0$ $3 x^{4} - 8 x^{3} + 8 x^{2} - 8 x + 3 = 0$ $3 x^{2} - 8 x + 8 - \frac{8}{x} + \frac{3}{x^{2}} = 0$ $3 (x^{2} + \frac{1}{x^{2}}) - 8 (x + \frac{1}{x}) + 8 = 0$ ${(x + \frac{1}{x})}^{2} = 2 + x^{2} + \frac{1}{x^{2}}$ $\Rightarrow x + \frac{1}{x} = t$ $\Rightarrow 3 (t^{2} - 2) - 8 t + 8 = 0$ $3 t^{2} - 8 t + 2 = 0$ $t_{1 / 2} = \frac{8 \pm \sqrt{64 - 24}}{6} = \frac{8 \pm 4 \sqrt{10}}{6} = \frac{4 \pm 2 \sqrt{10}}{3}$ $x^{2} - t x + 1 = 0$ $x_{1 / 2} = \frac{t \pm \sqrt{t^{2} - 4}}{2}$ $3 t^{2} - 8 t + 2 = 0 \Rightarrow t^{2} = \frac{8}{3} t - \frac{2}{3}$ $\Rightarrow t^{2} - 4 = \frac{8 t - 14}{3} = \frac{32 \pm 16 \sqrt{10} - 14}{3} = 6 \pm \frac{16 \sqrt{10}}{3} > 0$ $t^{2} - 4 = \sqrt{\frac{324}{9}} \pm \sqrt{\frac{2560}{9}} > 0$ $\Rightarrow t^{2} - 4 = 6 + \frac{16}{3} \sqrt{10}$ $\Rightarrow x_{1 / 2} = \frac{1}{2} (\frac{4 + 2 \sqrt{10}}{3} \pm \sqrt{\frac{18 + 16 \sqrt{10}}{3}})$ $\Rightarrow x = - 1; \frac{1}{2} (\frac{4 + 2 \sqrt{10}}{3} \pm \sqrt{\frac{18 + 16 \sqrt{10}}{3}})$
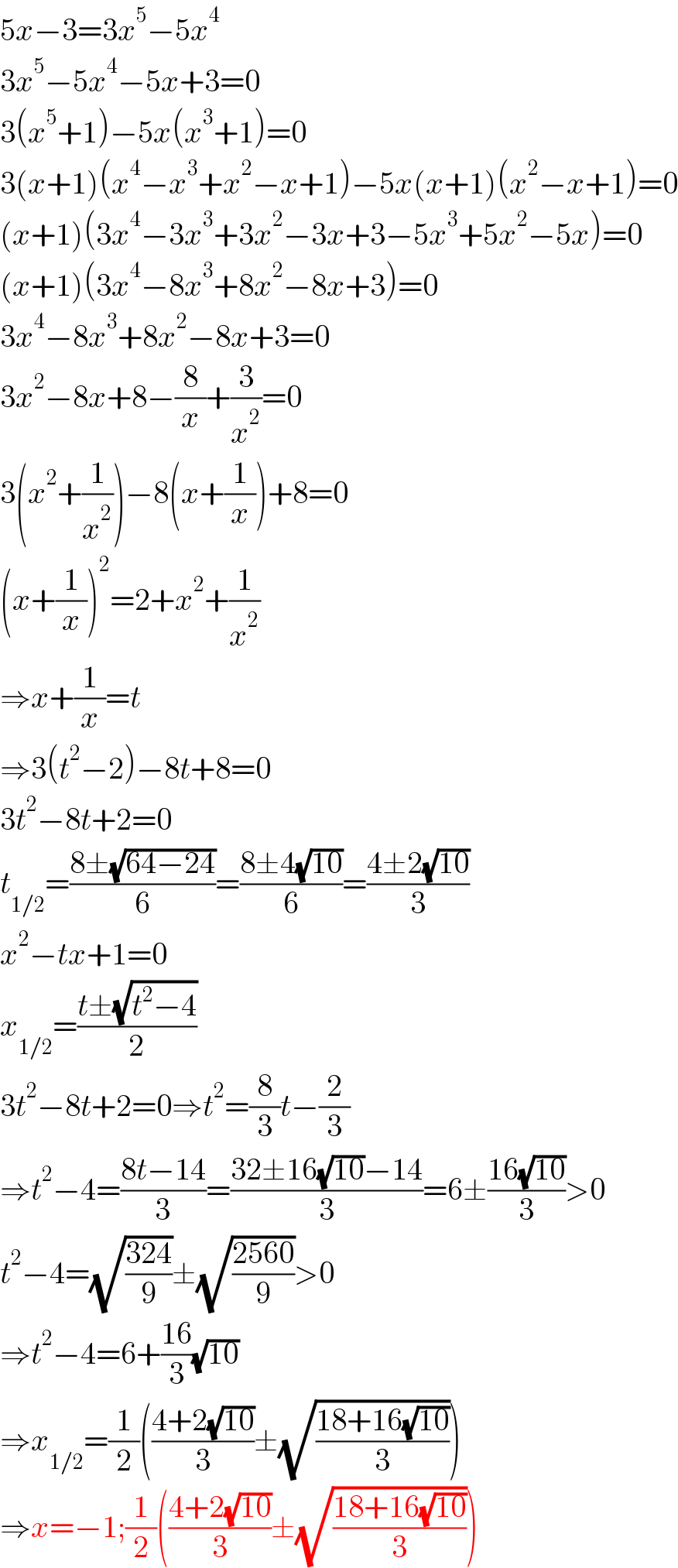
	Commented by mr W last updated on 14/Jul/22

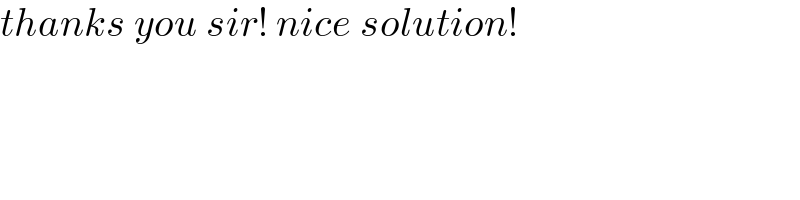
	$t h a n k s y o u s i r! n i c e s o l u t i o n!$
	Answered by Rasheed.Sindhi last updated on 14/Jul/22
	$((5x−3)/(3x−5))=x^4 (((5x−3)+(3x−5))/((5x−3)−(3x−5)))=((x^4 +1)/(x^4 −1)) [componendo-_(dividendo...) ((8x−8)/(2x+2))=((x^4 +1)/((x−1)(x+1)(x^2 +1))) ((8(x−1))/(2(x+1)))=((x^4 +1)/((x−1)(x+1)(x^2 +1))) 4(x−1)^2 (x+1)(x^2 +1)−(x+1)(x^4 +1)=0 (x+1){4(x−1)^2 (x^2 +1)−(x^4 +1)}=0 x+1=0 ∣ 3x^4 −8x^3 +8x^2 −8x+3=0 x=−1 ∣ 3(x^2 +(1/x^2 ))−8(x+(1/x))+8=0 x+(1/x)=y⇒x^2 +(1/x^2 )=y^2 −2 3(y^2 −2)−8y+8=0 3y^2 −8y+2=0 For solution of this equation please see sir mr W ′s answer.$
	$\frac{5 x - 3}{3 x - 5} = x^{4}$ $\frac{(5 x - 3) + (3 x - 5)}{(5 x - 3) - (3 x - 5)} = \frac{x^{4} + 1}{x^{4} - 1} [\underset{d i v i d e n d o . . .}{c o m p o n e n d o -}$ $\frac{8 x - 8}{2 x + 2} = \frac{x^{4} + 1}{(x - 1) (x + 1) (x^{2} + 1)}$ $\frac{8 (x - 1)}{2 (x + 1)} = \frac{x^{4} + 1}{(x - 1) (x + 1) (x^{2} + 1)}$ $4 {(x - 1)}^{2} (x + 1) (x^{2} + 1) - (x + 1) (x^{4} + 1) = 0$ $(x + 1) {4 {(x - 1)}^{2} (x^{2} + 1) - (x^{4} + 1)} = 0$ $x + 1 = 0 ∣ 3 x^{4} - 8 x^{3} + 8 x^{2} - 8 x + 3 = 0$ $x = - 1 ∣ 3 (x^{2} + \frac{1}{x^{2}}) - 8 (x + \frac{1}{x}) + 8 = 0$ $x + \frac{1}{x} = y \Rightarrow x^{2} + \frac{1}{x^{2}} = y^{2} - 2$ $3 (y^{2} - 2) - 8 y + 8 = 0$ $3 y^{2} - 8 y + 2 = 0$ $F o r s o l u t i o n o f t h i s e q u a t i o n p l e a s e$ $s e e s i r m r W^{'} s a n s w e r .$
	Answered by mr W last updated on 14/Jul/22

	$3 x^{5} + 3 - 5 x^{4} - 5 x = 0$ $3 (x^{5} + 1) - 5 x (x^{3} + 1) = 0$ $(x + 1) [3 (x^{4} - x^{3} + x^{2} - x + 1) - 5 x (x^{2} - x + 1)] = 0$ $(x + 1) [3 x^{4} + 3 - 8 x^{3} + 8 x^{2} - 8 x] = 0$ $(x + 1) [3 (x^{2} + \frac{1}{x^{2}}) - 8 (x + \frac{1}{x}) + 8] = 0$ $(x + 1) [3 {(x + \frac{1}{x})}^{2} - 8 (x + \frac{1}{x}) + 2] = 0$ $x + 1 = 0$ $\Rightarrow x = - 1 ✓$ $3 {(x + \frac{1}{x})}^{2} - 8 (x + \frac{1}{x}) + 2 = 0$ $\Rightarrow x + \frac{1}{x} = \frac{4 + \sqrt{10}}{3} (\frac{4 - \sqrt{10}}{3} < 2 r e j e c t e d)$ $x^{2} - \frac{4 + \sqrt{10}}{3} x + 1 = 0$ $\Rightarrow x = \frac{4 + \sqrt{10} \pm \sqrt{8 \sqrt{10} - 10}}{6} ✓$
	Answered by Tawa11 last updated on 14/Jul/22

	$Great sirs$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum