Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 173706 by infinityaction last updated on 16/Jul/22

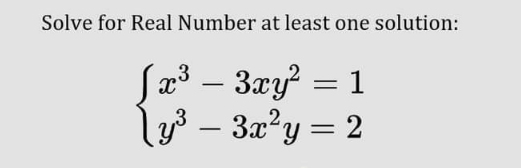
Commented by Frix last updated on 16/Jul/22

exact solution possible but not useable shortest way I found put y=cx ⇒ { ((x^3 =T_1 )),((x^3 =T_2 )) :} T_1 =T_2 ⇒ c_(1, 2, 3) but we get a 3^(rd) degree with 3 real solutions using the trigonometric method and these are not useable (try if you don′t believe) I approximated x_1 ≈−1.01832∧y_1 ≈−0.820363 x_2 ≈−0.201294∧y_2 ≈1.29207 x_3 ≈1.21962∧y_3 ≈−0.471711

$$\mathrm{exact}\:\mathrm{solution}\:\mathrm{possible}\:\mathrm{but}\:\mathrm{not}\:\mathrm{useable} \\ $$$$\mathrm{shortest}\:\mathrm{way}\:\mathrm{I}\:\mathrm{found}\:\mathrm{put}\:{y}={cx}\:\Rightarrow\:\begin{cases}{{x}^{\mathrm{3}} ={T}_{\mathrm{1}} }\\{{x}^{\mathrm{3}} ={T}_{\mathrm{2}} }\end{cases} \\ $$$${T}_{\mathrm{1}} ={T}_{\mathrm{2}} \:\Rightarrow\:{c}_{\mathrm{1},\:\mathrm{2},\:\mathrm{3}} \:\mathrm{but}\:\mathrm{we}\:\mathrm{get}\:\mathrm{a}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{degree}\:\mathrm{with} \\ $$$$\mathrm{3}\:\mathrm{real}\:\mathrm{solutions}\:\mathrm{using}\:\mathrm{the}\:{trigonometric} \\ $$$${method}\:\mathrm{and}\:\mathrm{these}\:\mathrm{are}\:\mathrm{not}\:\mathrm{useable}\:\left(\mathrm{try}\:\mathrm{if}\right. \\ $$$$\left.\mathrm{you}\:\mathrm{don}'\mathrm{t}\:\mathrm{believe}\right) \\ $$$$\mathrm{I}\:\mathrm{approximated} \\ $$$${x}_{\mathrm{1}} \approx−\mathrm{1}.\mathrm{01832}\wedge{y}_{\mathrm{1}} \approx−\mathrm{0}.\mathrm{820363} \\ $$$${x}_{\mathrm{2}} \approx−\mathrm{0}.\mathrm{201294}\wedge{y}_{\mathrm{2}} \approx\mathrm{1}.\mathrm{29207} \\ $$$${x}_{\mathrm{3}} \approx\mathrm{1}.\mathrm{21962}\wedge{y}_{\mathrm{3}} \approx−\mathrm{0}.\mathrm{471711} \\ $$

Answered by aleks041103 last updated on 16/Jul/22

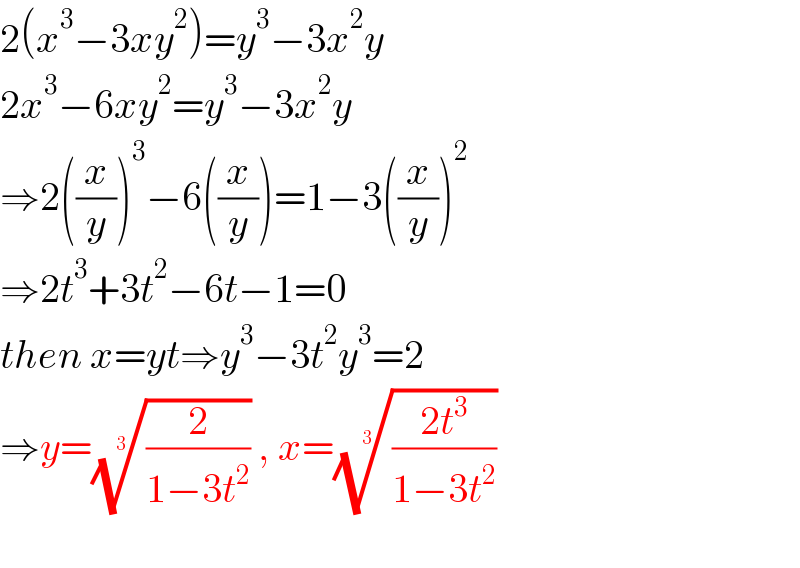
2(x^3 −3xy^2 )=y^3 −3x^2 y 2x^3 −6xy^2 =y^3 −3x^2 y ⇒2((x/y))^3 −6((x/y))=1−3((x/y))^2 ⇒2t^3 +3t^2 −6t−1=0 then x=yt⇒y^3 −3t^2 y^3 =2 ⇒y=((2/(1−3t^2 )))^(1/3) , x=(((2t^3 )/(1−3t^2 )))^(1/3)

$$\mathrm{2}\left({x}^{\mathrm{3}} −\mathrm{3}{xy}^{\mathrm{2}} \right)={y}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} {y} \\ $$$$\mathrm{2}{x}^{\mathrm{3}} −\mathrm{6}{xy}^{\mathrm{2}} ={y}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} {y} \\ $$$$\Rightarrow\mathrm{2}\left(\frac{{x}}{{y}}\right)^{\mathrm{3}} −\mathrm{6}\left(\frac{{x}}{{y}}\right)=\mathrm{1}−\mathrm{3}\left(\frac{{x}}{{y}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{t}^{\mathrm{3}} +\mathrm{3}{t}^{\mathrm{2}} −\mathrm{6}{t}−\mathrm{1}=\mathrm{0} \\ $$$${then}\:{x}={yt}\Rightarrow{y}^{\mathrm{3}} −\mathrm{3}{t}^{\mathrm{2}} {y}^{\mathrm{3}} =\mathrm{2} \\ $$$$\Rightarrow{y}=\sqrt[{\mathrm{3}}]{\frac{\mathrm{2}}{\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} }}\:,\:{x}=\sqrt[{\mathrm{3}}]{\frac{\mathrm{2}{t}^{\mathrm{3}} }{\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} }} \\ $$$$ \\ $$

Commented by aleks041103 last updated on 16/Jul/22

for t we don′t have exact sols t≈−2.586;−0.156;1.241 ⇒ (x,y)=(1.22,0.472);(−0.201,1.292);(−1.018,−0.820)

$${for}\:{t}\:{we}\:{don}'{t}\:{have}\:{exact}\:{sols} \\ $$$${t}\approx−\mathrm{2}.\mathrm{586};−\mathrm{0}.\mathrm{156};\mathrm{1}.\mathrm{241} \\ $$$$\Rightarrow \\ $$$$\left({x},{y}\right)=\left(\mathrm{1}.\mathrm{22},\mathrm{0}.\mathrm{472}\right);\left(−\mathrm{0}.\mathrm{201},\mathrm{1}.\mathrm{292}\right);\left(−\mathrm{1}.\mathrm{018},−\mathrm{0}.\mathrm{820}\right) \\ $$

Answered by puissant last updated on 17/Jul/22

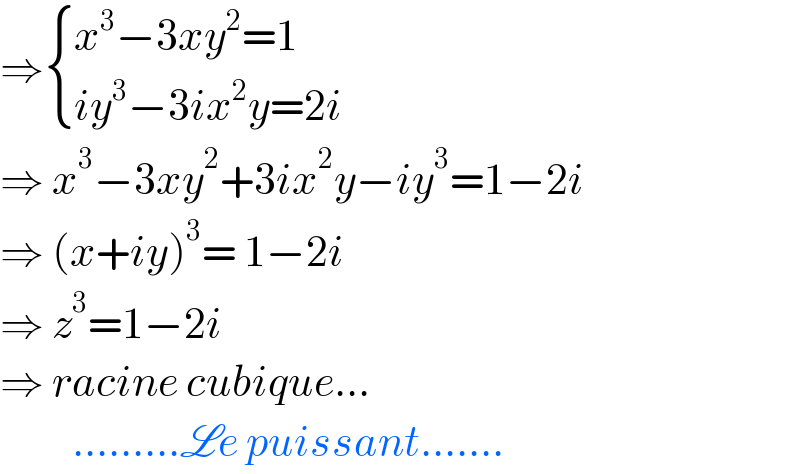
⇒ { ((x^3 −3xy^2 =1)),((iy^3 −3ix^2 y=2i)) :} ⇒ x^3 −3xy^2 +3ix^2 y−iy^3 =1−2i ⇒ (x+iy)^3 = 1−2i ⇒ z^3 =1−2i ⇒ racine cubique... .........Le puissant.......

$$\Rightarrow\begin{cases}{{x}^{\mathrm{3}} −\mathrm{3}{xy}^{\mathrm{2}} =\mathrm{1}}\\{{iy}^{\mathrm{3}} −\mathrm{3}{ix}^{\mathrm{2}} {y}=\mathrm{2}{i}}\end{cases} \\ $$$$\Rightarrow\:{x}^{\mathrm{3}} −\mathrm{3}{xy}^{\mathrm{2}} +\mathrm{3}{ix}^{\mathrm{2}} {y}−{iy}^{\mathrm{3}} =\mathrm{1}−\mathrm{2}{i} \\ $$$$\Rightarrow\:\left({x}+{iy}\right)^{\mathrm{3}} =\:\mathrm{1}−\mathrm{2}{i} \\ $$$$\Rightarrow\:{z}^{\mathrm{3}} =\mathrm{1}−\mathrm{2}{i}\: \\ $$$$\Rightarrow\:{racine}\:{cubique}... \\ $$$$\:\:\:\:\:\:\:\:\:.........\mathscr{L}{e}\:{puissant}....... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com