Question Number 173707 by dragan91 last updated on 16/Jul/22
$$\mathrm{Let}\:\mathrm{x},\mathrm{y}\in\mathbb{R}\:\mathrm{such}\:\mathrm{that}\:\mathrm{2x}^{\mathrm{2}} +\mathrm{3y}^{\mathrm{2}} =\mathrm{5} \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{and} \\ $$$$\mathrm{maximum}\:\mathrm{of}\:\mathrm{expression}: \\ $$$$\mathrm{P}=\mathrm{x}^{\mathrm{3}} −\mathrm{y}^{\mathrm{3}} +\mathrm{x}−\mathrm{2y} \\ $$
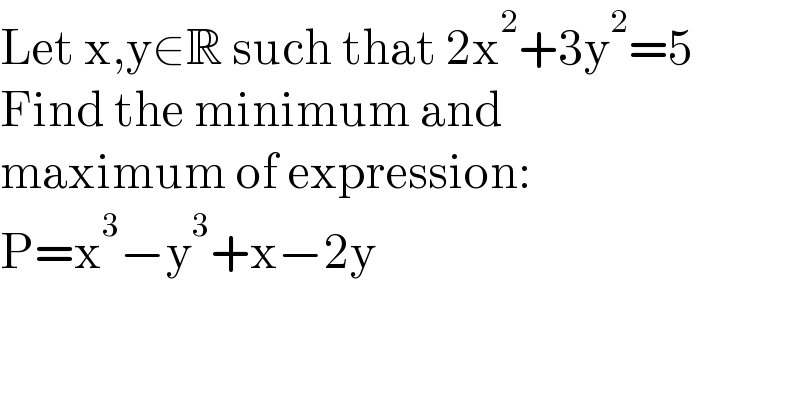
Answered by a.lgnaoui last updated on 17/Jul/22
$$ \\ $$$$\frac{{d}\left(\mathrm{P}\right)}{{dx}}+\frac{{d}\left(\mathrm{P}\right)}{{dy}}=\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{3}{y}^{\mathrm{2}} −\mathrm{2} \\ $$$$=\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3}{y}^{\mathrm{2}} −\mathrm{1}\:\:\:\:\mathrm{3}{y}^{\mathrm{2}} =\mathrm{5}−\mathrm{2}{x}^{\mathrm{2}} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}−\left(\mathrm{5}−\mathrm{2}{x}^{\mathrm{2}} \right)=\mathrm{5}{x}^{\mathrm{2}} −\mathrm{6}\:\: \\ $$$${the}\:{maximum}\:\:{and}\:{minimum}\:{of}\:\:\mathrm{P}\:{verify}\:\:\mathrm{P}'\left({x}\right)=\mathrm{0} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} −\mathrm{6}=\mathrm{0}\:\:\:\:{x}=\pm\sqrt{\frac{\mathrm{6}}{\mathrm{5}}}\: \\ $$$${x}=\pm\sqrt{\frac{\mathrm{6}}{\mathrm{5}}}\:\:\:\:\:{y}=\sqrt{\left(\mathrm{5}−\mathrm{2}\frac{\mathrm{6}}{\mathrm{5}}\right)/\mathrm{3}}=\sqrt{\frac{\mathrm{13}}{\mathrm{15}}} \\ $$$${m}=\left(−\sqrt{\frac{\mathrm{6}}{\mathrm{5}},}\sqrt{\frac{\mathrm{13}}{\mathrm{15}}}\:\right)\:\:{max}=\left(+\sqrt{\frac{\mathrm{6}}{\mathrm{5}}},\sqrt{\frac{\mathrm{13}}{\mathrm{15}}}\right) \\ $$
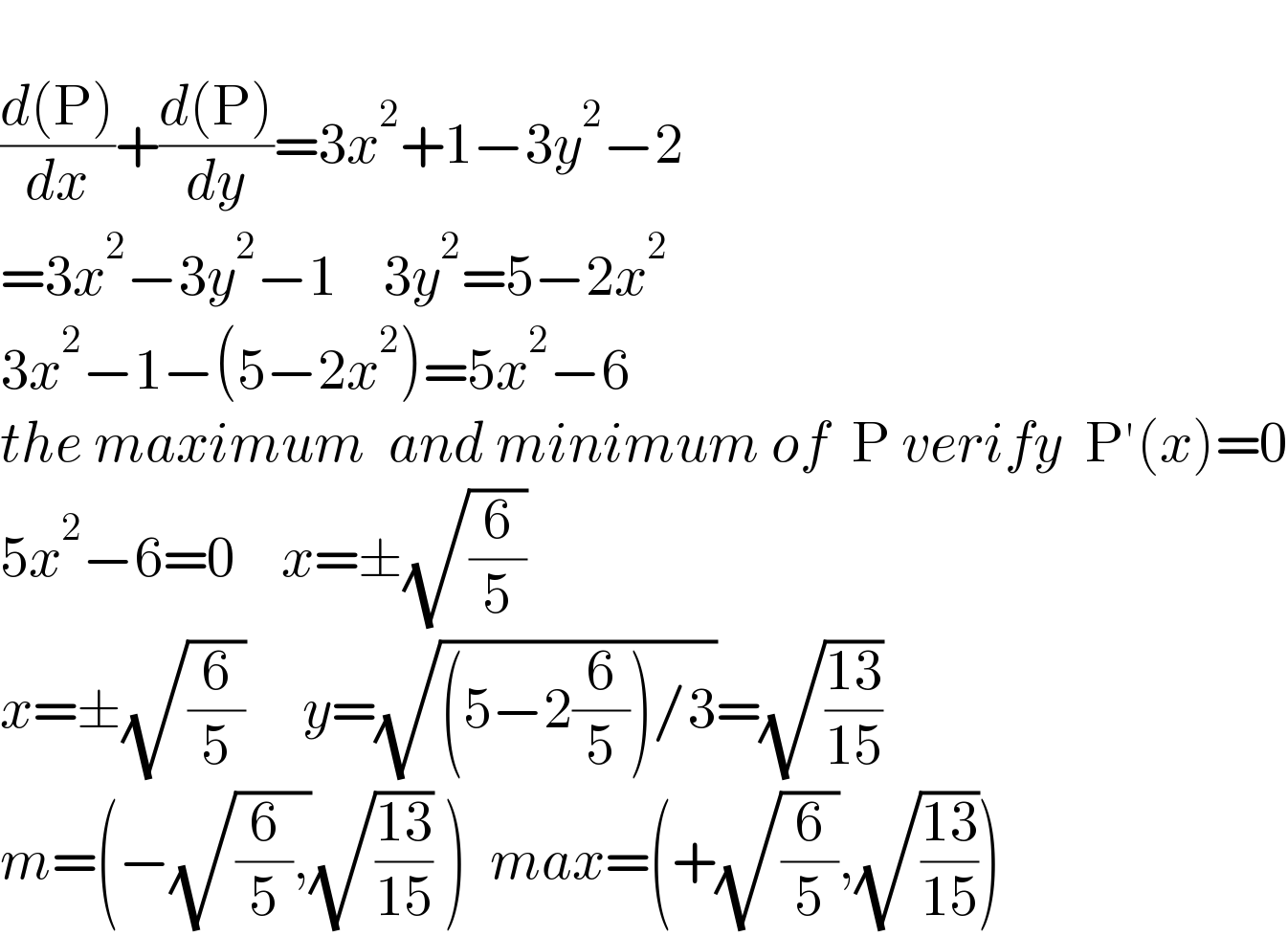
Commented by mr W last updated on 17/Jul/22
$${i}\:{think}\:{your}\:{method}\:{is}\:{wrong}. \\ $$$${for}\:{conditional}\:{extremums}\:{it}\:{doesn}'{t} \\ $$$${hold}\:{that}\:\frac{\partial{P}}{\partial{x}}=\mathrm{0}\:\wedge\:\frac{\partial{P}}{\partial{y}}=\mathrm{0},\:{or}\:\frac{\partial{P}}{\partial{x}}+\frac{\partial{P}}{\partial{y}}=\mathrm{0} \\ $$$${as}\:{you}\:{said}. \\ $$
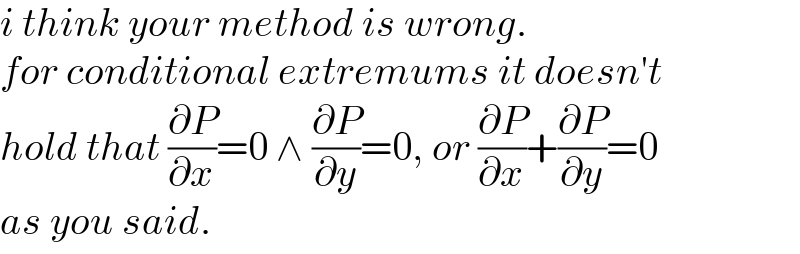
Answered by mr W last updated on 17/Jul/22
![G=x^3 −y^3 +x−2y+λ(2x^2 +3y^2 −5) (∂G/∂x)=3x^2 +1+4λx=0 ⇒x=((−2λ±(√(4λ^2 −3)))/3) (∂G/∂y)=−3y^2 −2+6λy=0 ⇒y=((3λ±(√(9λ^2 −6)))/3) (∂G/∂λ)=2x^2 +3y^2 −5=0 ⇒2[((−2λ±(√(4λ^2 −3)))/3)]^2 +3[((3λ±(√(9λ^2 −6)))/3)]^2 −5=0 that′s 4 equations which all can′t be solved exactly. we get approximately λ=−1.3191, P=5.8033=max λ=0.8872, P=−4.9111 λ=−0.8872, P=4.9111 λ=1.3191, P=−5.8033=min](Q173745.png)
$${G}={x}^{\mathrm{3}} −{y}^{\mathrm{3}} +{x}−\mathrm{2}{y}+\lambda\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} −\mathrm{5}\right) \\ $$$$\frac{\partial{G}}{\partial{x}}=\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}+\mathrm{4}\lambda{x}=\mathrm{0}\:\Rightarrow{x}=\frac{−\mathrm{2}\lambda\pm\sqrt{\mathrm{4}\lambda^{\mathrm{2}} −\mathrm{3}}}{\mathrm{3}} \\ $$$$\frac{\partial{G}}{\partial{y}}=−\mathrm{3}{y}^{\mathrm{2}} −\mathrm{2}+\mathrm{6}\lambda{y}=\mathrm{0}\:\Rightarrow{y}=\frac{\mathrm{3}\lambda\pm\sqrt{\mathrm{9}\lambda^{\mathrm{2}} −\mathrm{6}}}{\mathrm{3}} \\ $$$$\frac{\partial{G}}{\partial\lambda}=\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} −\mathrm{5}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\left[\frac{−\mathrm{2}\lambda\pm\sqrt{\mathrm{4}\lambda^{\mathrm{2}} −\mathrm{3}}}{\mathrm{3}}\right]^{\mathrm{2}} +\mathrm{3}\left[\frac{\mathrm{3}\lambda\pm\sqrt{\mathrm{9}\lambda^{\mathrm{2}} −\mathrm{6}}}{\mathrm{3}}\right]^{\mathrm{2}} −\mathrm{5}=\mathrm{0} \\ $$$${that}'{s}\:\mathrm{4}\:{equations}\:{which}\:{all}\:{can}'{t} \\ $$$${be}\:{solved}\:{exactly}. \\ $$$${we}\:{get}\:{approximately} \\ $$$$\lambda=−\mathrm{1}.\mathrm{3191},\:{P}=\mathrm{5}.\mathrm{8033}={max} \\ $$$$\lambda=\mathrm{0}.\mathrm{8872},\:{P}=−\mathrm{4}.\mathrm{9111} \\ $$$$\lambda=−\mathrm{0}.\mathrm{8872},\:{P}=\mathrm{4}.\mathrm{9111} \\ $$$$\lambda=\mathrm{1}.\mathrm{3191},\:{P}=−\mathrm{5}.\mathrm{8033}={min} \\ $$
Commented by mr W last updated on 17/Jul/22
Commented by Tawa11 last updated on 17/Jul/22
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by a.lgnaoui last updated on 17/Jul/22
$${thank}\:{you}\:{professor} \\ $$
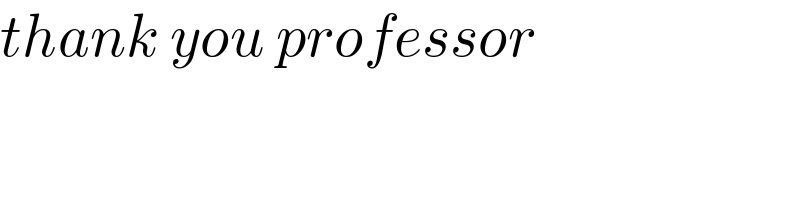
Answered by MJS_new last updated on 17/Jul/22
![2x^2 +3y^2 =5 ⇒ y=σ((√(3(5−2x^2 )))/3)∧σ=±1 P(x)=x(x^2 +1)+σ(((2x^2 −11)(√(3(5−2x^2 ))))/9) P ′(x)=0 3x^2 +1−σ((2(√3)x(2x^2 −7))/(3(√(5−2x^2 ))))=0 ⇒ x^6 −((211)/(70))x^4 +(8/5)x^2 −(3/(14))=0 t=x^2 t^3 −((211)/(70))t^2 +(8/5)t−(3/(14))=0 good luck! t=(3/(14)) is a solution t=(3/(14))∨t=(7/5)±((2(√6))/5) now it′s easy to get min (P(x)) =−(((9+44(√6))(√5))/(45)) at x=−(((1+(√6))(√5))/5)∧y=(((3−2(√6))(√5))/(15)) max (P(x))=(((9+44(√6))(√5))/(45)) at x=(((1+(√6))(√5))/5)∧y=−(((3−2(√6))(√5))/(15)) [approximated values ≈±5.80272 at x≈±1.54266 ∧y≈±.283083]](Q173753.png)
$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} =\mathrm{5}\:\Rightarrow\:{y}=\sigma\frac{\sqrt{\mathrm{3}\left(\mathrm{5}−\mathrm{2}{x}^{\mathrm{2}} \right)}}{\mathrm{3}}\wedge\sigma=\pm\mathrm{1} \\ $$$${P}\left({x}\right)={x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)+\sigma\frac{\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{11}\right)\sqrt{\mathrm{3}\left(\mathrm{5}−\mathrm{2}{x}^{\mathrm{2}} \right)}}{\mathrm{9}} \\ $$$${P}\:'\left({x}\right)=\mathrm{0} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}−\sigma\frac{\mathrm{2}\sqrt{\mathrm{3}}{x}\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{7}\right)}{\mathrm{3}\sqrt{\mathrm{5}−\mathrm{2}{x}^{\mathrm{2}} }}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${x}^{\mathrm{6}} −\frac{\mathrm{211}}{\mathrm{70}}{x}^{\mathrm{4}} +\frac{\mathrm{8}}{\mathrm{5}}{x}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{14}}=\mathrm{0} \\ $$$${t}={x}^{\mathrm{2}} \\ $$$${t}^{\mathrm{3}} −\frac{\mathrm{211}}{\mathrm{70}}{t}^{\mathrm{2}} +\frac{\mathrm{8}}{\mathrm{5}}{t}−\frac{\mathrm{3}}{\mathrm{14}}=\mathrm{0} \\ $$$$\mathrm{good}\:\mathrm{luck}!\:{t}=\frac{\mathrm{3}}{\mathrm{14}}\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution} \\ $$$${t}=\frac{\mathrm{3}}{\mathrm{14}}\vee{t}=\frac{\mathrm{7}}{\mathrm{5}}\pm\frac{\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{5}} \\ $$$$\mathrm{now}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{get} \\ $$$${min}\:\left({P}\left({x}\right)\right)\:=−\frac{\left(\mathrm{9}+\mathrm{44}\sqrt{\mathrm{6}}\right)\sqrt{\mathrm{5}}}{\mathrm{45}}\:\mathrm{at}\:{x}=−\frac{\left(\mathrm{1}+\sqrt{\mathrm{6}}\right)\sqrt{\mathrm{5}}}{\mathrm{5}}\wedge{y}=\frac{\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{6}}\right)\sqrt{\mathrm{5}}}{\mathrm{15}} \\ $$$${max}\:\left({P}\left({x}\right)\right)=\frac{\left(\mathrm{9}+\mathrm{44}\sqrt{\mathrm{6}}\right)\sqrt{\mathrm{5}}}{\mathrm{45}}\:\mathrm{at}\:{x}=\frac{\left(\mathrm{1}+\sqrt{\mathrm{6}}\right)\sqrt{\mathrm{5}}}{\mathrm{5}}\wedge{y}=−\frac{\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{6}}\right)\sqrt{\mathrm{5}}}{\mathrm{15}} \\ $$$$\left[\mathrm{approximated}\:\mathrm{values}\:\approx\pm\mathrm{5}.\mathrm{80272}\:\mathrm{at}\:{x}\approx\pm\mathrm{1}.\mathrm{54266}\:\wedge{y}\approx\pm.\mathrm{283083}\right] \\ $$
Commented by Tawa11 last updated on 17/Jul/22
$$\mathrm{Great}\:\mathrm{sir} \\ $$