4sin^( 2) (x)− 4sin(x)=cos^( 2) (x)−2cos(x) , 0<x<(π/2) . Find sin(x)=?


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 173787 by mnjuly1970 last updated on 18/Jul/22

$4 {s i n}^{2} (x) - 4 s i n (x) = {c o s}^{2} (x) - 2 c o s (x)$ $, 0 < x < \frac{π}{2} . F i n d s i n (x) = ?$
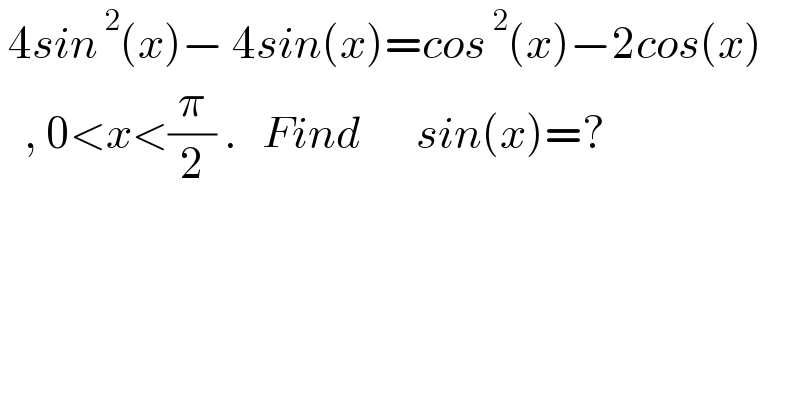
Commented byinfinityaction last updated on 18/Jul/22

$\frac{1}{\sqrt{5}}$
Commented bysom(math1967) last updated on 18/Jul/22

$\frac{3}{5} a l s o$
Commented byinfinityaction last updated on 18/Jul/22

${4 \sin}^{2} x - 4 \sin x + 1 = \cos^{2} x - 2 \cos x + 1$ ${(1 - 2 \sin x)}^{2} = {(1 - \cos x)}^{2}$ ${(1 - 2 \sin x)}^{2} - {(1 - \cos x)}^{2} = 0$ $(\cos x - 2 \sin x) (2 - 2 \sin x - \cos x) = 0$ $i f \cos x - 2 \sin x = 0 \Rightarrow \tan x = \frac{1}{2}$ $\sin x = \frac{1}{\sqrt{5}}$ $2 - 2 \sin x = \sqrt{1 - \sin^{2} x}$ ${5 \sin}^{2} x - 8 \sin x + 3 = 0$ $(\sin x - 1) (5 \sin x - 3) = 0$ $\sin x = 1 (r e j e c t e d)$ $\sin x = \frac{3}{5}$
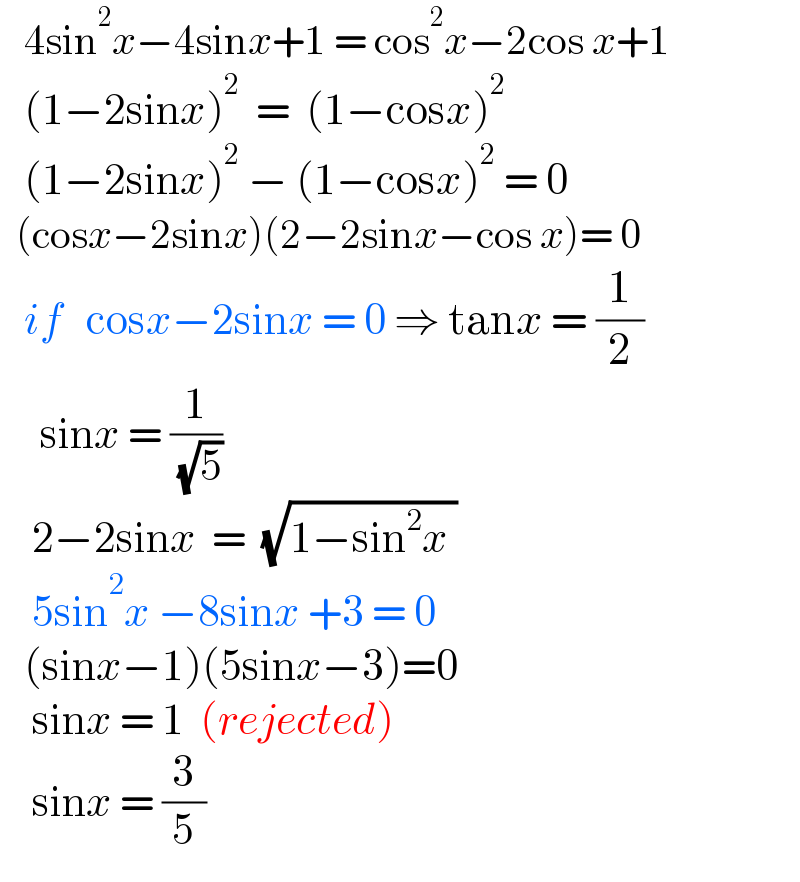
Commented bymnjuly1970 last updated on 18/Jul/22

$t h a n k y o u s o m u c h s i r . .$
Commented byMJS_new last updated on 18/Jul/22

$why do you reject 1 ?$
Commented byinfinityaction last updated on 18/Jul/22

$g i v e n i n t h e q u e s t i o n$ $0 < x < \frac{π}{2}$
Commented byTawa11 last updated on 18/Jul/22

$Great sirs$
Commented byMJS_new last updated on 18/Jul/22

$ok {didn}^{'} t notice . . .$
Commented byinfinityaction last updated on 18/Jul/22

$n o p r o b l e m s i r y o u r a l g e b r a$ $i s v e r y g o o d$ $i a m s t u d e n t o f u n d e r g r u a t e$ $s o c a n y o u s u g g e s t m e a n$ $a l g e b r a b o o k ? ?$
Commented byMJS_new last updated on 18/Jul/22

$sorry I {can}^{'} t . I studied math more than 20$ $years ago but I became a musician . math is$ $only my recreational sport now . . .$
Commented byinfinityaction last updated on 19/Jul/22

$o k s i r t h a n k s$
	Answered by MJS_new last updated on 18/Jul/22
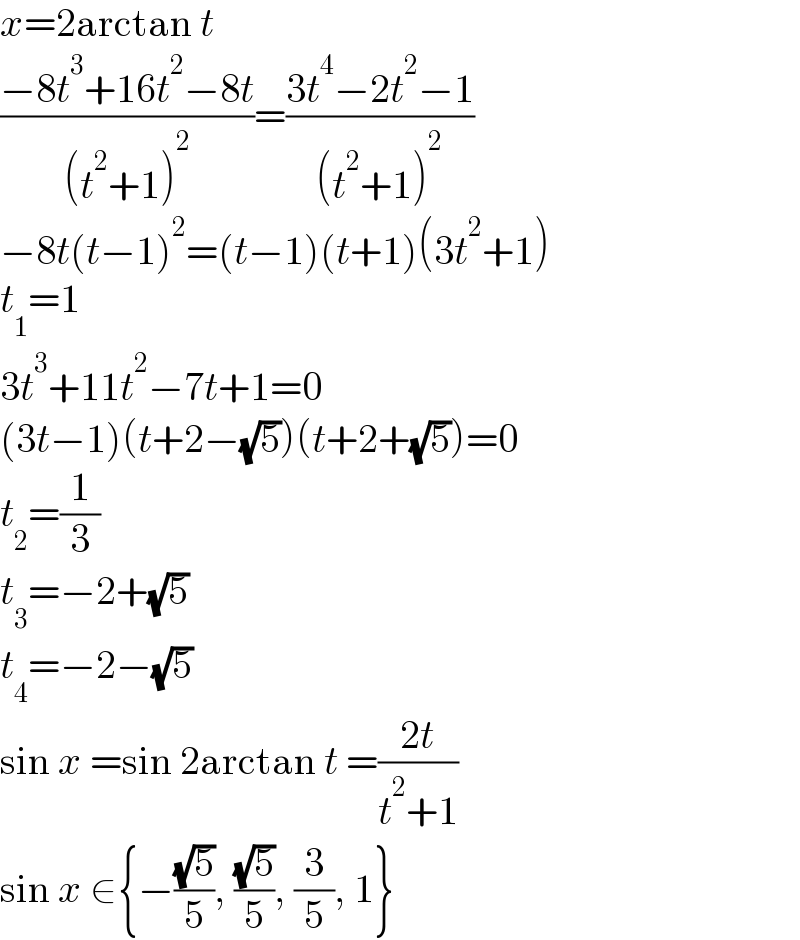
	$x=2arctan t ((−8t^3 +16t^2 −8t)/((t^2 +1)^2 ))=((3t^4 −2t^2 −1)/((t^2 +1)^2 )) −8t(t−1)^2 =(t−1)(t+1)(3t^2 +1) t_1 =1 3t^3 +11t^2 −7t+1=0 (3t−1)(t+2−(√5))(t+2+(√5))=0 t_2 =(1/3) t_3 =−2+(√5) t_4 =−2−(√5) sin x =sin 2arctan t =((2t)/(t^2 +1)) sin x ∈{−((√5)/5), ((√5)/5), (3/5), 1}$
	$x = 2 \arctan t$ $\frac{- 8 t^{3} + 16 t^{2} - 8 t}{{(t^{2} + 1)}^{2}} = \frac{3 t^{4} - 2 t^{2} - 1}{{(t^{2} + 1)}^{2}}$ $- 8 t {(t - 1)}^{2} = (t - 1) (t + 1) (3 t^{2} + 1)$ $t_{1} = 1$ $3 t^{3} + 11 t^{2} - 7 t + 1 = 0$ $(3 t - 1) (t + 2 - \sqrt{5}) (t + 2 + \sqrt{5}) = 0$ $t_{2} = \frac{1}{3}$ $t_{3} = - 2 + \sqrt{5}$ $t_{4} = - 2 - \sqrt{5}$ $\sin x = \sin 2 \arctan t = \frac{2 t}{t^{2} + 1}$ $\sin x \in {- \frac{\sqrt{5}}{5}, \frac{\sqrt{5}}{5}, \frac{3}{5}, 1}$
	Answered by a.lgnaoui last updated on 18/Jul/22

	$4 \sin^{2} (x) - 4 \sin (x) = 1 - \sin^{2} (x) - 2 \sqrt{1 - \sin^{2} (x)}$ $p o s i n s \sin (x) = z$ $5 z^{2} - 4 z - 1 = - 2 \sqrt{1 - z^{2}}$ ${[z - 1]}^{2} {[5 z + 1]}^{2} = 4 (1 - z^{2})$ $(1 - z) {(5 z + 1)}^{2} = 4 (1 + z)$ $(1 - z) (25 z^{2} + 10 z + 1) = 4 z + 4$ $25 z^{2} + 10 z + 1 - 25 z^{3} - 10 z^{2} - z - 4 z - 4 = 0$ $- 25 z^{3} + 15 z^{2} - 5 z - 3 = 0$ $25 z^{3} - 15 z^{2} + 5 z + 3 = 0$ $z^{3} - \frac{3}{5} z^{2} + \frac{z}{5} + \frac{3}{25} = 0$ $Z = z + 1 / 5$ $Z^{3} = z^{3} + \frac{3}{5} z^{2} + \frac{3}{25} z + \frac{1}{125}$ $- \frac{3}{5} Z^{2} = \frac{- 3}{5} z^{2} + - \frac{6}{25} z + \frac{- 3}{125}$ $Z = z + \frac{1}{5}$ $Z^{3} + (\frac{2}{25}) Z + \frac{22}{125} = 0 p = \frac{2}{25} q = \frac{22}{125}$ $p^{3} = (4 \times 8 / 5^{6}) / 27 + (4 \times 11^{2}) /$ $Δ = 484 / 5^{6} + \frac{32}{27 \times 5^{6}} = \frac{484 \times 27 + 32}{3^{3} \times 5^{6}} = \frac{13068 + 32}{} = \frac{13100}{421875} = 0, 031 \Rightarrow \sqrt{Δ} = 0, 176$ $q = \frac{22}{125} = 0, 176 \Rightarrow \frac{q}{2} = 0, 088$ $= - q / 2 \pm [^{3} \sqrt{\frac{- q}{2} \pm (4 p^{3} + 27 q^{2}) / 27)}] / 2 \sqrt{0, 176 - 0, 088}$ $Z = 0, 088 + [^{3} \sqrt{0, 088 + 0, 176}] / 2$ $Z = 0, 088 + [^{3} \sqrt{- 0, 088 + 0, 176}] / 2$ $Z = 0, 64 e t Z = - 0, 56$ $z = Z - \frac{1}{5} \Rightarrow \sin (x) = 0, 44$ $\sin (x) = 0, 36$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum