Question Number 173829 by mnjuly1970 last updated on 19/Jul/22
![If , x∈ [0 , 1] , ∣ (√(1−x^( 2) )) −ax−b ∣≤ (((√2) −1)/2) find the values of ( a , b ) a , b∈ R.](Q173829.png)
$$ \\ $$$$\:\:\:\:{If}\:\:,\:{x}\in\:\left[\mathrm{0}\:,\:\mathrm{1}\right]\: \\ $$$$\:\:\:\:\:\:,\:\:\:\:\mid\:\sqrt{\mathrm{1}−{x}^{\:\mathrm{2}} }\:−{ax}−{b}\:\mid\leqslant\:\frac{\sqrt{\mathrm{2}}\:−\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:{find}\:{the}\:{values}\:{of}\:\:\left(\:{a}\:,\:{b}\:\right) \\ $$$$\:\:\:{a}\:,\:{b}\in\:\mathbb{R}. \\ $$$$ \\ $$
Commented by kaivan.ahmadi last updated on 19/Jul/22
$${we}\:{can}\:{find}\:{b},\:{easily} \\ $$$${let}\:{f}\left({x}\right)=\mid\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }−{ax}−{b}\mid \\ $$$${f}\left(\mathrm{0}\right)=\mid\mathrm{1}−{b}\mid\leqslant\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{1}−\sqrt{\mathrm{2}}}{\mathrm{2}}\leqslant\mathrm{1}−{b}\leqslant\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{2}}\Rightarrow \\ $$$$\Rightarrow\frac{\mathrm{1}−\sqrt{\mathrm{2}}}{\mathrm{2}}\leqslant{b}−\mathrm{1}\leqslant\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{3}−\sqrt{\mathrm{2}}}{\mathrm{2}}\leqslant{b}\leqslant\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
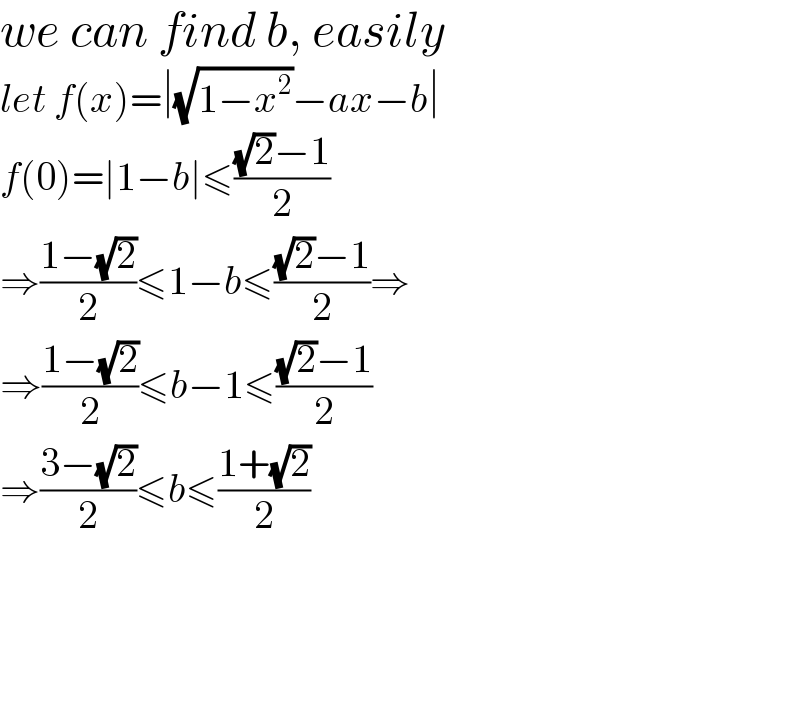
Answered by mahdipoor last updated on 19/Jul/22
![f(x)=(√(1−x^2 ))−ax−b (df/dx)=((−x)/( (√(1−x^2 ))))−a=0 or ∄ critical point in [0,1] ⇒ 0,1, (if a<0) ((−a)/( (√(1+a^2 )))) ∣f∣≤(((√2)−1)/2)=c ⇒ −c≤f≤c { ((x=0 ⇒ −c≤1−b≤c)),((x=1 ⇒ −c≤a+b≤c)),((x=((−a)/( (√(1+a^2 )))) ⇒ −c≤(√(1+a^2 ))−b≤c)) :} ⇒^((I)) { ((1−c≤b≤1+c (I))),((1−2c≤a≤2c+1 )),((−2(√(c^2 +c))≤a≤2(√(c^2 +c)))) :} ⇒ { ((1−c≤b≤1+c)),((−2(√(c^2 −c))≤1−2c≤a≤2(√(c^2 +c))≤2c+1)) :} a<0 & { ((((3−(√2))/2)≤b≤(((√2)+1)/2))),((2−(√2)≤a≤(√2))) :} ⇒ ∄ if a≥0 : critical point in [0,1] ⇒ 0,1 { ((x=0 ⇒ −c≤1−b≤c ⇒1−c≤b≤1+c)),((x=1 ⇒ −c≤a+b≤c ⇒1−2c≤a≤2c+1 )) :} ⇒ a≥0 & { ((((3−(√2))/2)≤b≤(((√2)+1)/2))),((2−(√2)≤a≤(√2))) :} ⇒⇒ { ((((3−(√2))/2)≤b≤(((√2)+1)/2))),((2−(√2)≤a≤(√2))) :}](Q173853.png)
$${f}\left({x}\right)=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }−{ax}−{b} \\ $$$$\frac{{df}}{{dx}}=\frac{−{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}−{a}=\mathrm{0}\:{or}\:\nexists\:\: \\ $$$${critical}\:{point}\:{in}\:\left[\mathrm{0},\mathrm{1}\right]\:\Rightarrow\:\mathrm{0},\mathrm{1},\:\left({if}\:{a}<\mathrm{0}\right)\:\frac{−{a}}{\:\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }} \\ $$$$\mid{f}\mid\leqslant\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{2}}={c}\:\Rightarrow\:−{c}\leqslant{f}\leqslant{c} \\ $$$$\begin{cases}{{x}=\mathrm{0}\:\Rightarrow\:−{c}\leqslant\mathrm{1}−{b}\leqslant{c}}\\{{x}=\mathrm{1}\:\Rightarrow\:−{c}\leqslant{a}+{b}\leqslant{c}}\\{{x}=\frac{−{a}}{\:\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}\:\Rightarrow\:−{c}\leqslant\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }−{b}\leqslant{c}}\end{cases} \\ $$$$\overset{\left(\mathrm{I}\right)} {\Rightarrow}\begin{cases}{\mathrm{1}−{c}\leqslant{b}\leqslant\mathrm{1}+{c}\:\:\:\:\:\left(\mathrm{I}\right)}\\{\mathrm{1}−\mathrm{2}{c}\leqslant{a}\leqslant\mathrm{2}{c}+\mathrm{1}\:}\\{−\mathrm{2}\sqrt{{c}^{\mathrm{2}} +{c}}\leqslant{a}\leqslant\mathrm{2}\sqrt{{c}^{\mathrm{2}} +{c}}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\mathrm{1}−{c}\leqslant{b}\leqslant\mathrm{1}+{c}}\\{−\mathrm{2}\sqrt{{c}^{\mathrm{2}} −{c}}\leqslant\mathrm{1}−\mathrm{2}{c}\leqslant{a}\leqslant\mathrm{2}\sqrt{{c}^{\mathrm{2}} +{c}}\leqslant\mathrm{2}{c}+\mathrm{1}}\end{cases} \\ $$$${a}<\mathrm{0}\:\:\&\:\begin{cases}{\frac{\mathrm{3}−\sqrt{\mathrm{2}}}{\mathrm{2}}\leqslant{b}\leqslant\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\mathrm{2}}}\\{\mathrm{2}−\sqrt{\mathrm{2}}\leqslant{a}\leqslant\sqrt{\mathrm{2}}}\end{cases}\:\Rightarrow\:\nexists \\ $$$${if}\:{a}\geqslant\mathrm{0}\:: \\ $$$${critical}\:{point}\:{in}\:\left[\mathrm{0},\mathrm{1}\right]\:\Rightarrow\:\mathrm{0},\mathrm{1} \\ $$$$\begin{cases}{{x}=\mathrm{0}\:\Rightarrow\:−{c}\leqslant\mathrm{1}−{b}\leqslant{c}\:\Rightarrow\mathrm{1}−{c}\leqslant{b}\leqslant\mathrm{1}+{c}}\\{{x}=\mathrm{1}\:\Rightarrow\:−{c}\leqslant{a}+{b}\leqslant{c}\:\Rightarrow\mathrm{1}−\mathrm{2}{c}\leqslant{a}\leqslant\mathrm{2}{c}+\mathrm{1}\:}\end{cases} \\ $$$$\Rightarrow\:{a}\geqslant\mathrm{0}\:\&\:\begin{cases}{\frac{\mathrm{3}−\sqrt{\mathrm{2}}}{\mathrm{2}}\leqslant{b}\leqslant\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\mathrm{2}}}\\{\mathrm{2}−\sqrt{\mathrm{2}}\leqslant{a}\leqslant\sqrt{\mathrm{2}}}\end{cases} \\ $$$$\Rightarrow\Rightarrow\begin{cases}{\frac{\mathrm{3}−\sqrt{\mathrm{2}}}{\mathrm{2}}\leqslant{b}\leqslant\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\mathrm{2}}}\\{\mathrm{2}−\sqrt{\mathrm{2}}\leqslant{a}\leqslant\sqrt{\mathrm{2}}}\end{cases} \\ $$
Commented by mnjuly1970 last updated on 20/Jul/22
$${zendeh}\:{bashid}\:{ostad} \\ $$$$\:{sepas}... \\ $$
Commented by mahdipoor last updated on 20/Jul/22
$${sharmande}\:{mikonid}\:{mano}\:, \\ $$$$\left.\:{man}\:{ostad}\:{nistam}\:...\::\right) \\ $$