Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 173834 by mnjuly1970 last updated on 19/Jul/22

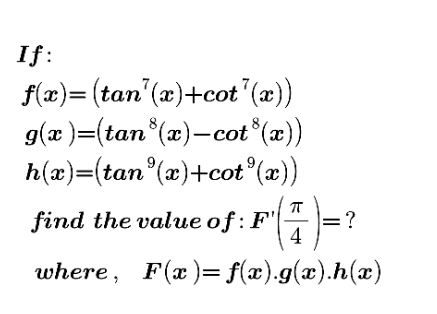
Commented by infinityaction last updated on 20/Jul/22

$$\mathit{f}\left(\mathit{x}\right)\mathit{g}\left(\mathit{x}\right)\mathit{h}\left(\mathit{x}\right)=({\mathbf{tan}}^7\mathit{x}+{\mathbf{cot}}^7\mathit{x})({\mathbf{tan}}^8\mathit{x}-{\mathbf{cot}}^8\mathit{x})$$$$\times ({\mathbf{tan}}^9\mathit{x}+{\mathbf{cot}}^9\mathit{x})$$$$\mathit{F}\left(\mathit{x}\right)=({\mathbf{tan}}^{15}\mathit{x}-\mathbf{cot}\mathit{x}+\mathbf{tan}\mathit{x}-{\mathbf{cot}}^{15}\mathit{x})({\mathbf{tan}}^9+{\mathbf{cot}}^9\mathit{x})$$$$F\left(x\right)={\tan }^{24}x-{\tan }^{8}x+{\tan }^{10}x-{\cot }^{6}x$$$$+{\tan }^{6}x-{\cot }^{10}x+{\cot }^{8}x-{\cot }^{24}x$$$$F{}^{\prime }\left(x\right)={24\tan }^{23}x{\sec }^{2}x-{8\tan }^{7}x{\sec }^{2}x$$$$+{10\tan }^{9}x{\sec }^{2}x+{6\cot }^{5}x{\mathrm{cosec}}^{2}x$$$$+{6\tan }^{5}x{\sec }^{2}x+{10\cot }^{9}x{\mathrm{cosec}}^{2}x-$$$${8\cot }^{7}x{\mathrm{cosec}}^{2}x+{24\cot }^{23}x{\mathrm{cosec}}^{2}x$$$$F{}^{\prime }\left(x\right)=48-16+20+12+12+20-16+48$$$$\text{Prime causes double exponent: use braces to clarify}$$

Commented by Tawa11 last updated on 19/Jul/22

$$\mathrm{Great}\mathrm{sirs}$$

Answered by mahdipoor last updated on 19/Jul/22

$$P\left(x\right)=P_{a,\pm }\left(x\right)={tan}^a\left(x\right)\pm {cot}^a\left(x\right)$$$$\frac{dP}{dx}=a({tan}^{a-1}\left(x\right).\frac{1}{{cos}^{2}x}\mp {cot}^{a-1}\left(x\right).\frac{1}{{sin}^{2}x})$$$$\Rightarrow \{\begin{array}{l}P\left(\theta \right)=1\pm 1\\ P^{{}^{\prime }}\left(\theta \right)=2a(1\mp 1)\end{array}get\theta =\pi /4$$$$f\equiv P_{7,+}\Rightarrow f\left(\theta \right)=2D_{x}f\left(\theta \right)=0$$$$g\equiv P_{8,-}\Rightarrow g\left(\theta \right)=0D_{x}g\left(\theta \right)=32$$$$h\equiv P_{7,+}\Rightarrow h\left(\theta \right)=2D_{x}h\left(\theta \right)=0$$$$\frac{dF}{dx}\left(\theta \right)=\frac{d}{dx}\left(fgh\right)\left(\theta \right)=(f^{{}^{\prime }}gh+{fg}^{{}^{\prime }}h+{fgh}^{{}^{\prime }})\left(\theta \right)=$$$$0+2\times 32\times 2+0=128$$

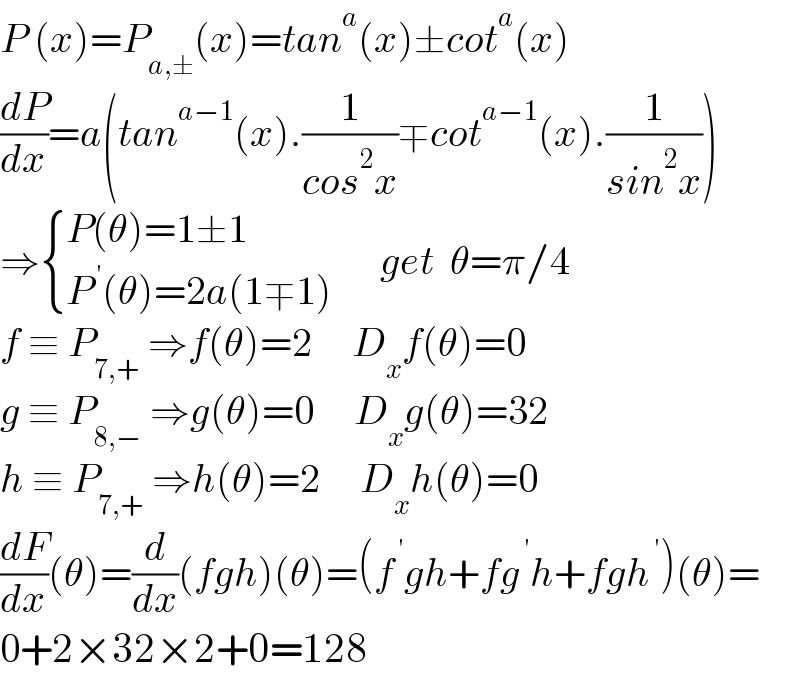
Commented by mnjuly1970 last updated on 19/Jul/22

$$verynicemamnonostad$$

Commented by mahdipoor last updated on 20/Jul/22

$$lotfdaridostad:)$$

Answered by mr W last updated on 20/Jul/22

$$F\left(x\right)=f\left(x\right)g\left(x\right)h\left(x\right)$$$$\ln F\left(x\right)=\ln f\left(x\right)+\ln g\left(x\right)+\ln h\left(x\right)$$$$\frac{F^{\prime }\left(x\right)}{F\left(x\right)}=\frac{f^{\prime }\left(x\right)}{f\left(x\right)}+\frac{g^{\prime }\left(x\right)}{g\left(x\right)}+\frac{h^{\prime }\left(x\right)}{h\left(x\right)}$$$$F^{\prime }\left(x\right)=g\left(x\right)h\left(x\right)f^{\prime }\left(x\right)+f\left(x\right)h\left(x\right)g^{\prime }\left(x\right)+f\left(x\right)g\left(x\right)h^{\prime }\left(x\right)$$$$f\left(\frac{\pi }{4}\right)=h\left(\frac{\pi }{4}\right)=2$$$$g\left(\frac{\pi }{4}\right)=0$$$$F^{\prime }\left(\frac{\pi }{4}\right)=f\left(\frac{\pi }{4}\right)h\left(\frac{\pi }{4}\right)g^{\prime }\left(\frac{\pi }{4}\right)=4\times g^{\prime }\left(\frac{\pi }{4}\right)$$$$=4\times {[\frac{8{\tan }^{7}x}{{\cos }^{2}x}+\frac{8{\cot }^{7}x}{{\sin }^{2}x}]}_{x=\frac{\pi }{4}}$$$$=32\times [\frac{1}{\frac{1}{2}}+\frac{1}{\frac{1}{2}}]$$$$=32\times 4=128$$

Commented by mnjuly1970 last updated on 20/Jul/22

$$reallynicesolutionmaster$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com