
Question and Answers Forum
Question Number 173836 by mathlove last updated on 19/Jul/22
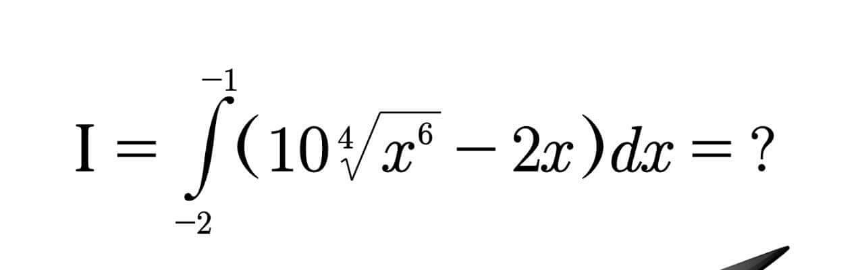
Commented by aleks041103 last updated on 21/Jul/22
![I=∫_(−2) ^(−1) (10(x^6 )^(1/4) −2x)dx= =10∫_(−2) ^(−1) (x^6 )^(1/4) dx − ∫_(−2) ^(−1) 2xdx= =10J−[x^2 ]_(−2) ^(−1) =16(√2)−(1−4)=3+16(√2) x^6 is even⇒J=∫_(−2) ^(−1) (x^6 )^(1/4) dx=∫_1 ^( 2) (x^6 )^(1/4) dx=∫_1 ^2 x^(3/2) dx= =[(2/5)x^(5/2) ]_1 ^2 =((8(√2))/5)](Q173938.png)
Answered by CElcedricjunior last updated on 19/Jul/22
![I=∫_(−2) ^(−1) (10(√x^3 )−2x)dx=∫_(−2) ^(−1) (10x^(3/2) −2x)dx or (√x^3 ) n′est definie en [−2;−1] alors I n′existe pas dans R mais dansC](Q173851.png)
Answered by a.lgnaoui last updated on 19/Jul/22
![I=10∫_(−2) ^(−1) x^(3/2) dx−2∫xdx I=10[(x^((3/2)+1) /((3/2)+1))]_(−2) ^(−1) −2[(x^2 /2)]_(−2) ^(−1) =4[x^2 (√x) ]_(−2) ^(−1) −[x^2 ]_(−2) ^(+1) =[x^2 (4(√x)−1)]_(−2) ^(−1) x<0⇒(√x)=(√(∣x∣i^2 ))=i(√(∣x∣)) I=[x^2 (4i(√(∣x∣))−1)]_(−2) ^(−1) =4i−1−16(√2)i+4 I=3+(4−16(√2))i=3−18,56i](Q173855.png)
| ||
Question and Answers Forum | ||
Question Number 173836 by mathlove last updated on 19/Jul/22 | ||
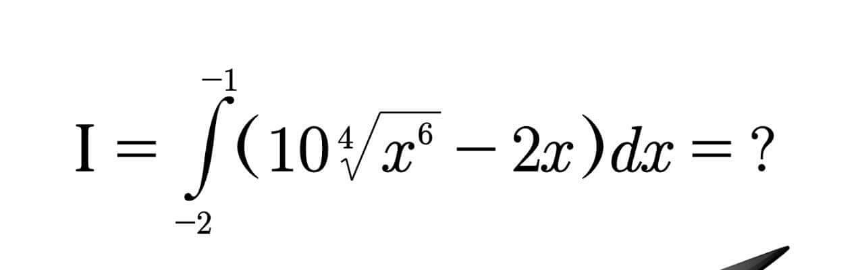 | ||
Commented by aleks041103 last updated on 21/Jul/22 | ||
![I=∫_(−2) ^(−1) (10(x^6 )^(1/4) −2x)dx= =10∫_(−2) ^(−1) (x^6 )^(1/4) dx − ∫_(−2) ^(−1) 2xdx= =10J−[x^2 ]_(−2) ^(−1) =16(√2)−(1−4)=3+16(√2) x^6 is even⇒J=∫_(−2) ^(−1) (x^6 )^(1/4) dx=∫_1 ^( 2) (x^6 )^(1/4) dx=∫_1 ^2 x^(3/2) dx= =[(2/5)x^(5/2) ]_1 ^2 =((8(√2))/5)](Q173938.png) | ||
Answered by CElcedricjunior last updated on 19/Jul/22 | ||
![I=∫_(−2) ^(−1) (10(√x^3 )−2x)dx=∫_(−2) ^(−1) (10x^(3/2) −2x)dx or (√x^3 ) n′est definie en [−2;−1] alors I n′existe pas dans R mais dansC](Q173851.png) | ||
| ||
Answered by a.lgnaoui last updated on 19/Jul/22 | ||
![I=10∫_(−2) ^(−1) x^(3/2) dx−2∫xdx I=10[(x^((3/2)+1) /((3/2)+1))]_(−2) ^(−1) −2[(x^2 /2)]_(−2) ^(−1) =4[x^2 (√x) ]_(−2) ^(−1) −[x^2 ]_(−2) ^(+1) =[x^2 (4(√x)−1)]_(−2) ^(−1) x<0⇒(√x)=(√(∣x∣i^2 ))=i(√(∣x∣)) I=[x^2 (4i(√(∣x∣))−1)]_(−2) ^(−1) =4i−1−16(√2)i+4 I=3+(4−16(√2))i=3−18,56i](Q173855.png) | ||
| ||