Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 173976 by savitar last updated on 22/Jul/22

$$$$$$B(a,b)={\int }_0^1{x}^{a-1}{(1-x)}^{b-1}dx$$$$\mathrm{\Gamma }\left(s\right)={\int }_0^{\mathrm{\infty }}{t}^{s-1}{e}^{-t}dt$$$$$$$$WhyB(a,b)=\frac{\mathrm{\Gamma }\left(a\right)\mathrm{\Gamma }\left(b\right)}{\mathrm{\Gamma }(a+b)}?$$$$$$$$$$$$$$$$$$

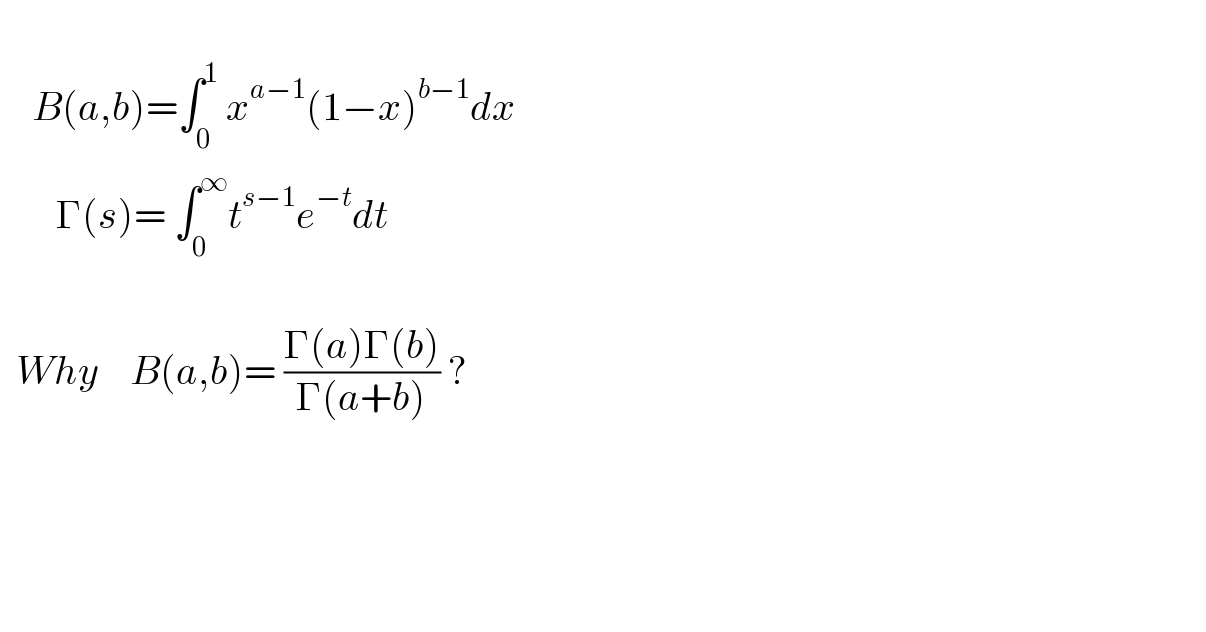
Answered by aleks041103 last updated on 22/Jul/22

$$Iff\left(x\right)=x^{a-1}andg\left(x\right)=x^{b-1}$$$$alsoh\left(t\right)=(f\ast g)\left(t\right)={\int }_0^{t}f\left(x\right)g(t-x)dxistheconvolution$$$$\Rightarrow h\left(t\right)={\int }_0^t{x}^{a-1}{(t-x)}^{b-1}dx$$$$x=ty\Rightarrow dx=tdy$$$$\Rightarrow h\left(t\right)={\int }_0^1{t}^{a-1}{y}^{a-1}{t}^{b-1}{(1-y)}^{b-1}tdy=$$$$=t^{a+b-1}{\int }_0^1{t}^{a-1}{(1-y)}^{b-1}dy=$$$$=B(a,b)t^{a+b-1}$$$$forconvolution:$$$$H\left(s\right)=F\left(s\right)G\left(s\right)$$$$whereF,G,Harethelaplacetransforms$$$$off,g,hrespectively.$$$$Since\mathcal{L}\left\{x^p\right\}\left(s\right)=\frac{\mathrm{\Gamma }(p+1)}{s^{p+1}},then$$$$H\left(s\right)=B(a,b)\frac{\mathrm{\Gamma }(a+b)}{s^{a+b}}$$$$F\left(s\right)=\frac{\mathrm{\Gamma }\left(a\right)}{s^a}andG\left(s\right)=\frac{\mathrm{\Gamma }\left(b\right)}{s^b}$$$$\Rightarrow \frac{\mathrm{\Gamma }\left(a\right)\mathrm{\Gamma }\left(b\right)}{s^{a+b}}=B(a,b)\frac{\mathrm{\Gamma }(a+b)}{s^{a+b}}$$$$\Rightarrow B(a,b)=\frac{\mathrm{\Gamma }\left(a\right)\mathrm{\Gamma }\left(b\right)}{\mathrm{\Gamma }(a+b)}$$

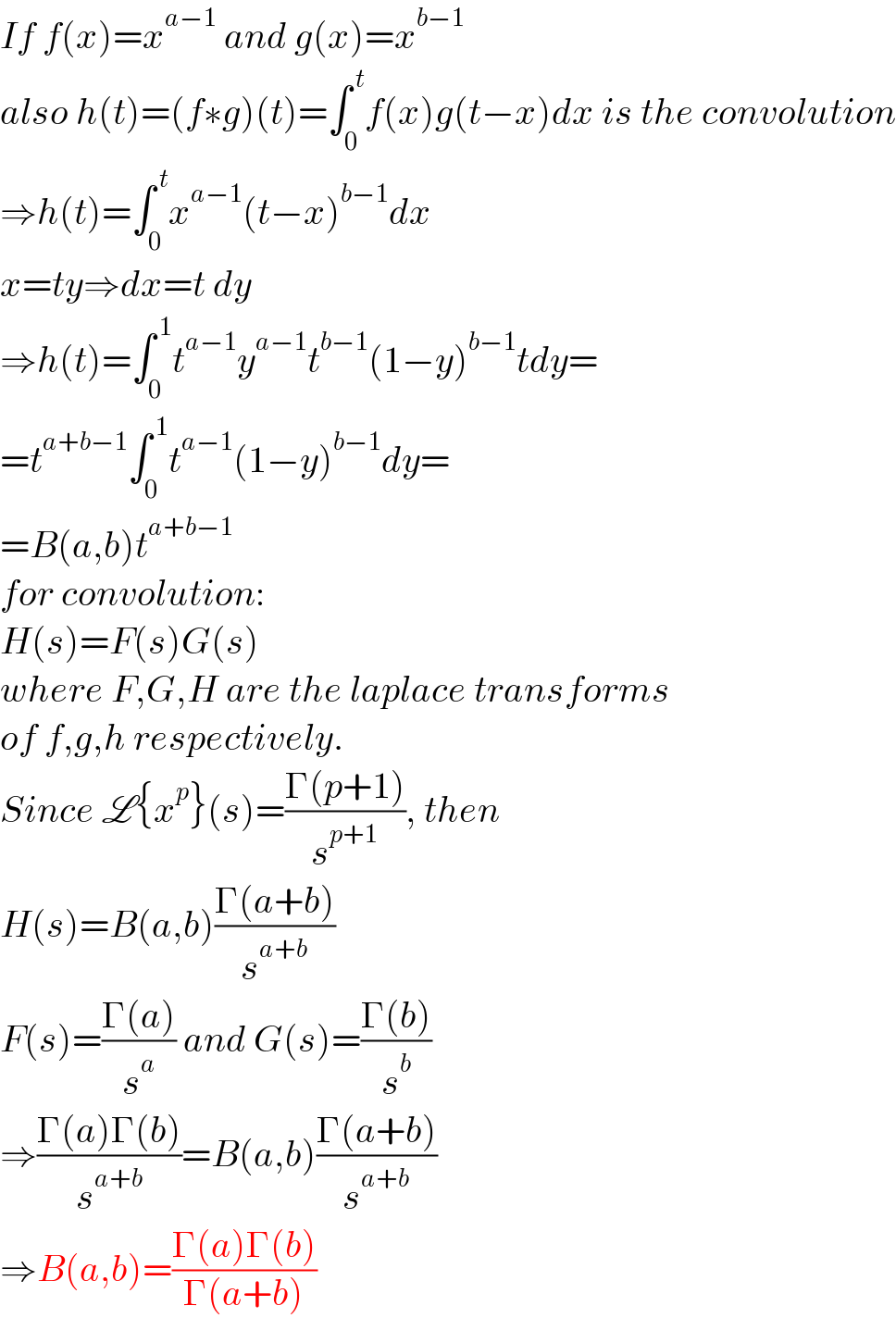
Commented by savitar last updated on 22/Jul/22

$$Verynicesir$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com