Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 174059 by mr W last updated on 23/Jul/22

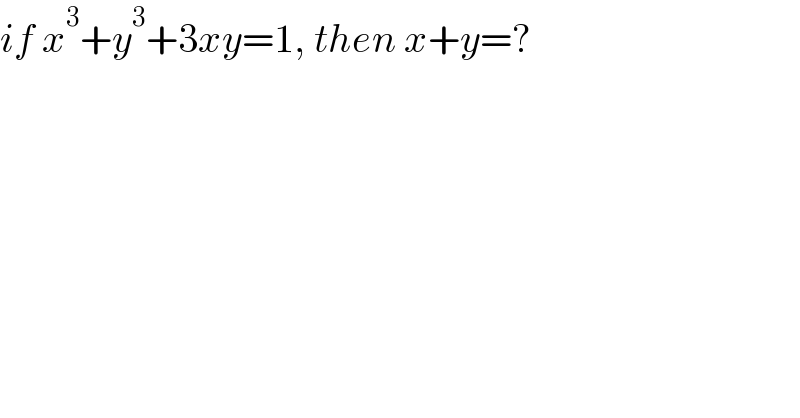
if x^3 +y^3 +3xy=1, then x+y=?

$${if}\:{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +\mathrm{3}{xy}=\mathrm{1},\:{then}\:{x}+{y}=? \\ $$

Commented by infinityaction last updated on 23/Jul/22

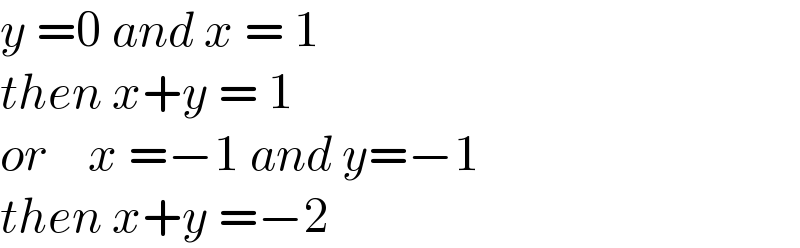
y =0 and x = 1 then x+y = 1 or x =−1 and y=−1 then x+y =−2

$${y}\:=\mathrm{0}\:{and}\:{x}\:=\:\mathrm{1} \\ $$$${then}\:{x}+{y}\:=\:\mathrm{1} \\ $$$${or}\:\:\:\:{x}\:=−\mathrm{1}\:{and}\:{y}=−\mathrm{1} \\ $$$${then}\:{x}+{y}\:=−\mathrm{2} \\ $$

Commented by Tawa11 last updated on 24/Jul/22

Great sirs

$$\mathrm{Great}\:\mathrm{sirs} \\ $$

Commented by dragan91 last updated on 24/Jul/22

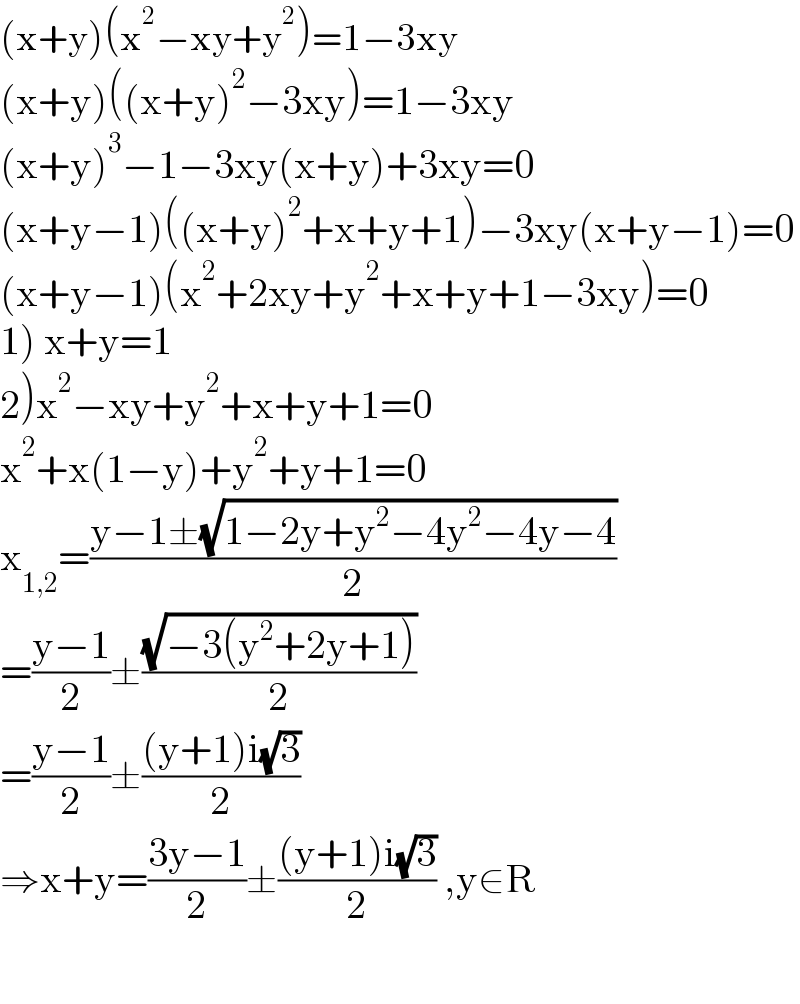
(x+y)(x^2 −xy+y^2 )=1−3xy (x+y)((x+y)^2 −3xy)=1−3xy (x+y)^3 −1−3xy(x+y)+3xy=0 (x+y−1)((x+y)^2 +x+y+1)−3xy(x+y−1)=0 (x+y−1)(x^2 +2xy+y^2 +x+y+1−3xy)=0 1) x+y=1 2)x^2 −xy+y^2 +x+y+1=0 x^2 +x(1−y)+y^2 +y+1=0 x_(1,2) =((y−1±(√(1−2y+y^2 −4y^2 −4y−4)))/2) =((y−1)/2)±((√(−3(y^2 +2y+1)))/2) =((y−1)/2)±(((y+1)i(√3))/2) ⇒x+y=((3y−1)/2)±(((y+1)i(√3))/2) ,y∈R

$$\left(\mathrm{x}+\mathrm{y}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{xy}+\mathrm{y}^{\mathrm{2}} \right)=\mathrm{1}−\mathrm{3xy} \\ $$$$\left(\mathrm{x}+\mathrm{y}\right)\left(\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} −\mathrm{3xy}\right)=\mathrm{1}−\mathrm{3xy} \\ $$$$\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{3}} −\mathrm{1}−\mathrm{3xy}\left(\mathrm{x}+\mathrm{y}\right)+\mathrm{3xy}=\mathrm{0} \\ $$$$\left(\mathrm{x}+\mathrm{y}−\mathrm{1}\right)\left(\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} +\mathrm{x}+\mathrm{y}+\mathrm{1}\right)−\mathrm{3xy}\left(\mathrm{x}+\mathrm{y}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\left(\mathrm{x}+\mathrm{y}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2xy}+\mathrm{y}^{\mathrm{2}} +\mathrm{x}+\mathrm{y}+\mathrm{1}−\mathrm{3xy}\right)=\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:\mathrm{x}+\mathrm{y}=\mathrm{1} \\ $$$$\left.\mathrm{2}\right)\mathrm{x}^{\mathrm{2}} −\mathrm{xy}+\mathrm{y}^{\mathrm{2}} +\mathrm{x}+\mathrm{y}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{x}\left(\mathrm{1}−\mathrm{y}\right)+\mathrm{y}^{\mathrm{2}} +\mathrm{y}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{x}_{\mathrm{1},\mathrm{2}} =\frac{\mathrm{y}−\mathrm{1}\pm\sqrt{\mathrm{1}−\mathrm{2y}+\mathrm{y}^{\mathrm{2}} −\mathrm{4y}^{\mathrm{2}} −\mathrm{4y}−\mathrm{4}}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{y}−\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{−\mathrm{3}\left(\mathrm{y}^{\mathrm{2}} +\mathrm{2y}+\mathrm{1}\right)}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{y}−\mathrm{1}}{\mathrm{2}}\pm\frac{\left(\mathrm{y}+\mathrm{1}\right)\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{x}+\mathrm{y}=\frac{\mathrm{3y}−\mathrm{1}}{\mathrm{2}}\pm\frac{\left(\mathrm{y}+\mathrm{1}\right)\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:,\mathrm{y}\in\mathrm{R} \\ $$$$ \\ $$

Answered by behi834171 last updated on 24/Jul/22

x+y=p,xy=q (x+y)[(x+y)^2 −3xy]+3xy=1 ⇒p(p^2 −3q)+3q=1⇒p^3 −3pq+3q−1=0 (p−1)(p^2 +p−3q+1)=0 ⇒p=1,p=((−1±(√(12q−3)))/2) ⇒x+y=p=1 .■ [only possibility,i think] [12q−3=0⇒q=(1/4),p=−(1/2) ⇒z^2 +(z/2)+(1/4)=0⇒4z^2 +2z+1=0 z=((−2±(√(4−16)))/8)=((−2±2(√3)i)/8)=−((1/4)∓i.((√3)/4)) ⇒ { ((x=−((1/4)+i.((√3)/4)))),((y=−((1/4)+i.((√3)/4)))) :} ⇒x+y=^? −(1/2) x^3 +y^3 =(x+y)[(x+y)^2 −3xy]= =(−(1/2))[(1/4)−(3/4)]=(1/4) ⇒x^3 +y^3 +3xy=(1/4)+3×(1/4)=1 ok ⇒x+y=−(1/2) [another possibility]]

$${x}+{y}={p},{xy}={q} \\ $$$$\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)\left[\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)^{\mathrm{2}} −\mathrm{3}\boldsymbol{{xy}}\right]+\mathrm{3}\boldsymbol{{xy}}=\mathrm{1} \\ $$$$\Rightarrow\boldsymbol{{p}}\left(\boldsymbol{{p}}^{\mathrm{2}} −\mathrm{3}\boldsymbol{{q}}\right)+\mathrm{3}\boldsymbol{{q}}=\mathrm{1}\Rightarrow\boldsymbol{{p}}^{\mathrm{3}} −\mathrm{3}\boldsymbol{{pq}}+\mathrm{3}\boldsymbol{{q}}−\mathrm{1}=\mathrm{0} \\ $$$$\left(\boldsymbol{{p}}−\mathrm{1}\right)\left(\boldsymbol{{p}}^{\mathrm{2}} +\boldsymbol{{p}}−\mathrm{3}\boldsymbol{{q}}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\boldsymbol{{p}}=\mathrm{1},\boldsymbol{{p}}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{12}\boldsymbol{{q}}−\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow\boldsymbol{{x}}+\boldsymbol{{y}}=\boldsymbol{{p}}=\mathrm{1}\:\:.\blacksquare\:\:\:\left[{only}\:{possibility},{i}\:{think}\right] \\ $$$$\left[\mathrm{12}\boldsymbol{{q}}−\mathrm{3}=\mathrm{0}\Rightarrow\boldsymbol{{q}}=\frac{\mathrm{1}}{\mathrm{4}},\boldsymbol{{p}}=−\frac{\mathrm{1}}{\mathrm{2}}\right. \\ $$$$\Rightarrow\boldsymbol{{z}}^{\mathrm{2}} +\frac{\boldsymbol{{z}}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0}\Rightarrow\mathrm{4}{z}^{\mathrm{2}} +\mathrm{2}{z}+\mathrm{1}=\mathrm{0} \\ $$$${z}=\frac{−\mathrm{2}\pm\sqrt{\mathrm{4}−\mathrm{16}}}{\mathrm{8}}=\frac{−\mathrm{2}\pm\mathrm{2}\sqrt{\mathrm{3}}\boldsymbol{{i}}}{\mathrm{8}}=−\left(\frac{\mathrm{1}}{\mathrm{4}}\mp\boldsymbol{{i}}.\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\right) \\ $$$$\Rightarrow\begin{cases}{\boldsymbol{{x}}=−\left(\frac{\mathrm{1}}{\mathrm{4}}+\boldsymbol{{i}}.\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\right)}\\{\boldsymbol{{y}}=−\left(\frac{\mathrm{1}}{\mathrm{4}}+\boldsymbol{{i}}.\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\right)}\end{cases}\:\:\:\:\Rightarrow\boldsymbol{{x}}+\boldsymbol{{y}}\overset{?} {=}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\boldsymbol{{x}}^{\mathrm{3}} +\boldsymbol{{y}}^{\mathrm{3}} =\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)\left[\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)^{\mathrm{2}} −\mathrm{3}\boldsymbol{{xy}}\right]= \\ $$$$=\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left[\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{3}}{\mathrm{4}}\right]=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\boldsymbol{{x}}^{\mathrm{3}} +\boldsymbol{{y}}^{\mathrm{3}} +\mathrm{3}\boldsymbol{{xy}}=\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{3}×\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{1}\:\:\boldsymbol{{ok}} \\ $$$$\left.\Rightarrow\boldsymbol{{x}}+\boldsymbol{{y}}=−\frac{\mathrm{1}}{\mathrm{2}}\:\:\left[\boldsymbol{{another}}\:\boldsymbol{{possibility}}\right]\right] \\ $$

Answered by MJS_new last updated on 24/Jul/22

x^3 +y^3 +3xy−1=0 (x+y−1)(x^2 −xy+y^2 +x+y+1)=0 (1) x+y=1 (2) y=((x−1)/2)±(((√3)(x+1))/2)i if x, y ∈R ⇒ x=−1∧y=−1 ⇒ x+y=−2 if x, y ∈C ⇒ x+y=((3x−1)/2)±(((√3)(x+1))/2)i ∧ x∈C

$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} +\mathrm{3}{xy}−\mathrm{1}=\mathrm{0} \\ $$$$\left({x}+{y}−\mathrm{1}\right)\left({x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} +{x}+{y}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\left(\mathrm{1}\right)\:{x}+{y}=\mathrm{1} \\ $$$$\left(\mathrm{2}\right)\:{y}=\frac{{x}−\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}\left({x}+\mathrm{1}\right)}{\mathrm{2}}\mathrm{i} \\ $$$$\:\:\:\:\:\mathrm{if}\:{x},\:{y}\:\in\mathbb{R}\:\Rightarrow\:{x}=−\mathrm{1}\wedge{y}=−\mathrm{1}\:\Rightarrow\:{x}+{y}=−\mathrm{2} \\ $$$$\:\:\:\:\:\mathrm{if}\:{x},\:{y}\:\in\mathbb{C}\:\Rightarrow\:{x}+{y}=\frac{\mathrm{3}{x}−\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}\left({x}+\mathrm{1}\right)}{\mathrm{2}}\mathrm{i}\:\wedge\:{x}\in\mathbb{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com