find all prime p and q such that p^2 − p = 37q^2 − q


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 174062 by Tawa11 last updated on 23/Jul/22

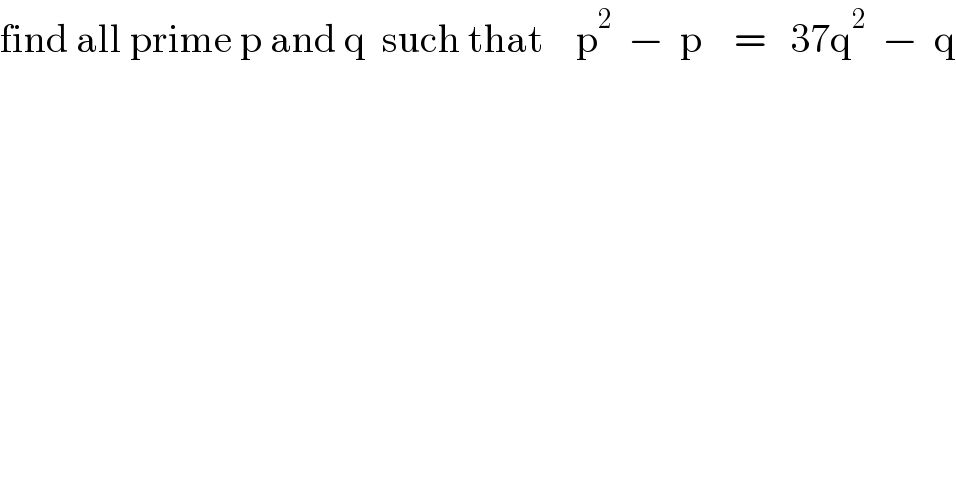
$find all prime p and q such that p^{2} - p = {37 q}^{2} - q$
Commented by Rasheed.Sindhi last updated on 24/Jul/22
$≪_• ^• SUCCESSFUL Approach_• ^• _(−) ^(−) ≫ p^ − p = q^ − q p^2 −q^2 =36q^2 +p−q p^2 −q^2 −(p−q)=36q^2 (p−q)(p+q−1)=36q^2 (((p−q)(p+q−1))/q^2 )=36 { (((((p−q)/q))(((p+q−1)/q))=36)),(((((p−q)/q^2 ))(p+q−1)=36)),(((p−q)(((p+q−1)/q^2 ))=36)) :} { ((^★ ((p/q)−1)((p/q)+((q−1)/q))=36 (false))),((^(★★) (((p−q)/q^2 ))(p+q−1)=36)),(((p−q)(((p+q−1)/q^2 ))=36 (only possible case))) :} ^★ q∣p⇒q=p [∵ p,q∈P] p=q⇒(p/q)=1 and this make^★ false. ^(★★) ((p−q)/q^2 ) is impossible as p,q∈P p−q=k ∧ ((p+q−1)/q^2 )=((36)/k) ; k∣36 p−q=k_((i)) ∧ p+q=((36q^2 )/k)+1_((ii)) (ii)−(i): 2q=(((36q^2 )/k)+1)−k 2qk=36q^2 +k−k^2 36q^2 −2kq+k−k^2 =0 q=((2k±(√(4k^2 −4(36)(k−k^2 ))))/(72)) =((2k±2(√(k^2 −36k+36k^2 )))/(72)) =((k±(√(37k^2 −36k)))/(36))∈P ∧ k∣36 Possible candidates for k: ±1,±2,±3,±4,±6,±9,±12,±18,±36 Only successful candidate for k is 36 k=36⇒ { ((q=7,p=43)),((q=−5,p=31)) :}$
$≪_{∙}^{∙} \underline{\overset{―}{SUCCESSFUL {Approach}_{∙}^{∙}}} ≫$ $p^{} - p = q^{} - q$ $p^{2} - q^{2} = 36 q^{2} + p - q$ $p^{2} - q^{2} - (p - q) = 36 q^{2}$ $(p - q) (p + q - 1) = 36 q^{2}$ $\frac{(p - q) (p + q - 1)}{q^{2}} = 36$ ${\begin{cases} (\frac{p - q}{q}) (\frac{p + q - 1}{q}) = 36 \\ (\frac{p - q}{q^{2}}) (p + q - 1) = 36 \\ (p - q) (\frac{p + q - 1}{q^{2}}) = 36 \end{cases}$ ${\begin{cases} ^{★} (\frac{p}{q} - 1) (\frac{p}{q} + \frac{q - 1}{q}) = 36 (f a l s e) \\ ^{★ ★} (\frac{p - q}{q^{2}}) (p + q - 1) = 36 \\ (p - q) (\frac{p + q - 1}{q^{2}}) = 36 (o n l y p o s s i b l e c a s e) \end{cases}$ $^{★} q ∣ p \Rightarrow q = p [∵ p, q \in P]$ $p = q \Rightarrow \frac{p}{q} = 1 a n d t h i s m a k e^{★} f a l s e .$ $^{★ ★} \frac{p - q}{q^{2}} i s i m p o s s i b l e a s p, q \in P$ $p - q = k \land \frac{p + q - 1}{q^{2}} = \frac{36}{k}; k ∣ 36$ $\underset{(i)}{\underset{⏟}{p - q = k}} \land \underset{(i i)}{p + q = \frac{36 q^{2}}{k} + 1}$ $(i i) - (i) :$ $2 q = (\frac{36 q^{2}}{k} + 1) - k$ $2 q k = 36 q^{2} + k - k^{2}$ $36 q^{2} - 2 k q + k - k^{2} = 0$ $q = \frac{2 k \pm \sqrt{4 k^{2} - 4 (36) (k - k^{2})}}{72}$ $= \frac{2 k \pm 2 \sqrt{k^{2} - 36 k + 36 k^{2}}}{72}$ $= \frac{k \pm \sqrt{37 k^{2} - 36 k}}{36} \in P \land k ∣ 36$ $P o s s i b l e c a n d i d a t e s f o r k :$ $\pm 1, \pm 2, \pm 3, \pm 4, \pm 6, \pm 9, \pm 12, \pm 18, \pm 36$ $O n l y s u c c e s s f u l c a n d i d a t e f o r k i s 36$ $k = 36 \Rightarrow {\begin{cases} q = 7, p = 43 \\ q = - 5, p = 31 \end{cases}$
Commented by Tawa11 last updated on 25/Jul/22

$Wow, God bless you sir .$
Commented by MathematicalUser2357 last updated on 26/Feb/25

${It}^{'} s so funny where : \underset{―}{q such that p^{2} - p = 37}$
	Answered by Rasheed.Sindhi last updated on 24/Jul/22

	$p^{2} - p = 37 q^{2} - q; p, q \in P$ $p (p - 1) = q (37 q - 1)$ $p = q \lor p ∣ (37 q - 1)$ $∙ p = q \land p - 1 = 37 q - 1 \Rightarrow p - 1 = 37 p - 1$ $\Rightarrow p = 0 \notin P$ $∴ p \neq q$ $∙ p ∣ (37 q - 1) \land p, q s a t i s f y t h e g i v e n r e l a t i o n .$ $q = 2 \Rightarrow 37 q - 1 = 73 \Rightarrow p = 73 \times$ $q = 3 \Rightarrow 37 q - 1 = 110 \Rightarrow p = 2, 5, 11 \times$ $q = 5 \Rightarrow 37 q - 1 = 184 \Rightarrow p = 2, 23 \times$ $q = \overset{✓}{7} \Rightarrow 37 q - 1 = 258 \Rightarrow p = \overset{\times}{2}, \overset{\times}{3}, \overset{✓}{43}$ $(p, q) = (43, 7)$ $C o n t i n u e$
	Answered by Rasheed.Sindhi last updated on 24/Jul/22

	$p^{2} - p = {37 q}^{2} - q$ $p^{2} - p + q - {37 q}^{2} = 0$ $p = \frac{1 \pm \sqrt{1 - 4 q (1 - 37 q)}}{2}$ $p = \frac{1 \pm \sqrt{{148 q}^{2} - 4 q + 1}}{2}$ $p = \frac{1 \pm \sqrt{\frac{37 ({148 q}^{2}) - 37 (4 q) + 37}{37}}}{2}$ $p = \frac{1 \pm \sqrt{\frac{74^{2} q^{2} - 148 q + 1 + 37 - 1}{37}}}{2}$ $p = \frac{1 \pm \sqrt{\frac{74^{2} q^{2} + 148 q + 1 - 296 q + 37 - 1}{37}}}{2}$ $p = \frac{1 \pm \sqrt{\frac{{(74 q + 1)}^{2} + 36 - 296 q}{37}}}{2}$ $p = \frac{1 \pm \sqrt{\frac{{(74 q + 1)}^{2} - 4 (74 q - 9)}{37}}}{2}$ $△ = \frac{{(74 q + 1)}^{2} - 4 (74 q - 9)}{37} is perfect square integer .$ $For q = 7, △ is 85^{2}$ $q = 7 \Rightarrow p = 43$ $. o . . . . . . .$
	Commented by Tawa11 last updated on 24/Jul/22

	$God bless you sir . I appreciate .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum