Question Number 174096 by mnjuly1970 last updated on 24/Jul/22
$$ \\ $$$$\:\:\:{f}\left({x}\right)=\:{ax}^{\:\mathrm{2}} +\:{bx}\:+{c}\:\:{is}\:{given} \\ $$$$\:\:\:\:\:\:{a}\:\neq\:{b}\:\neq\:{c}\:\:,\:{a}\:,\:{b}\:,\:{c}\:\in\:\mathbb{R}\: \\ $$$$\:\:\:\:\:\:\:{a}\neq\mathrm{0}\:\:\:{and}\:\:\:: \\ $$$$\:\:\:\:\:\:\:\:{f}\left({ax}\:+\:{b}\:\right)={f}\:\left({bx}\:+\:{c}\right) \\ $$$$\:\:\:\:\:\:{find}\::\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\:\left({f}\left({b}\right)\:\:−\:{f}\left({a}\:\right)\right)=? \\ $$
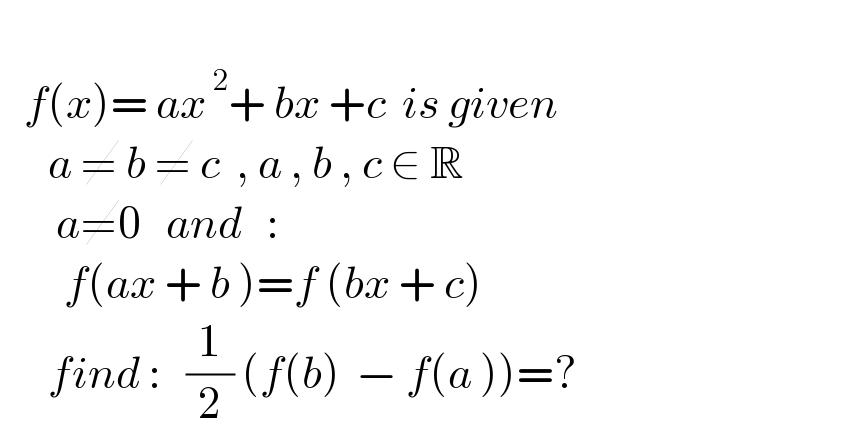
Answered by mahdipoor last updated on 24/Jul/22
![if f(x)=axx+bx+c and Max/min f=f(((−b)/(2a))) f(m)=f(n)⇔((m+n)/2)=((−b)/(2a)) ⇒⇒(((ax+b)+(bx+c))/2)=((−b)/(2a))⇒ a+b=0 and b+c=((−b)/a) ⇒ a=k b=−k c=1+k ⇒ f(x)=kxx−kx+1+k (1/2)([k(−k)^2 −k(−k)+1+k]− [k(k^2 )−k(k)+1+k])=k^2 =a^2](Q174097.png)
$${if}\:\:\:{f}\left({x}\right)={axx}+{bx}+{c}\:\:\:{and}\:\:\: \\ $$$${Max}/{min}\:{f}={f}\left(\frac{−{b}}{\mathrm{2}{a}}\right) \\ $$$${f}\left({m}\right)={f}\left({n}\right)\Leftrightarrow\frac{{m}+{n}}{\mathrm{2}}=\frac{−{b}}{\mathrm{2}{a}} \\ $$$$\Rightarrow\Rightarrow\frac{\left({ax}+{b}\right)+\left({bx}+{c}\right)}{\mathrm{2}}=\frac{−{b}}{\mathrm{2}{a}}\Rightarrow \\ $$$${a}+{b}=\mathrm{0}\:\:{and}\:\:\:{b}+{c}=\frac{−{b}}{{a}}\:\Rightarrow \\ $$$${a}={k}\:\:\:\:{b}=−{k}\:\:\:\:{c}=\mathrm{1}+{k}\:\Rightarrow\: \\ $$$${f}\left({x}\right)={kxx}−{kx}+\mathrm{1}+{k}\: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\left[{k}\left(−{k}\right)^{\mathrm{2}} −{k}\left(−{k}\right)+\mathrm{1}+{k}\right]−\right. \\ $$$$\left.\left[{k}\left({k}^{\mathrm{2}} \right)−{k}\left({k}\right)+\mathrm{1}+{k}\right]\right)={k}^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 24/Jul/22
$${thank}\:{you}\:{master}\:..{faghat}\:=\:{a}^{\:\mathrm{2}} \\ $$$$\:\:\:\:{typo}... \\ $$
Commented by mahdipoor last updated on 24/Jul/22
$${tnx}\:,\:{i}\:{edited}\: \\ $$
Answered by cortano1 last updated on 25/Jul/22
![f(ax+b)=a(ax+b)^2 +b(ax+b)+c f(bx+c)=a(bx+c)^2 +b(bx+c)+c { ((f(ax+b)=a^3 x^2 +2a^2 bx+ab^2 +abx+b^2 +c)),((f(bx+c)=ab^2 x^2 +2abcx+ac^2 +b^2 x+bc+c)) :} { ((a^2 =b^2 ⇒ { ((a=b(rejected))),((a=−b)) :})),((2a^2 b+ab=b^2 +2abc)),((ab^2 +b^2 +c=ac^2 +bc+c)) :} for a=−b ⇒ { ((−2a^3 −a^2 =a^2 −2a^2 c)),((a^3 +a^2 +c=ac−ac+c)) :} ⇒a^2 (a+1)=0⇒a=−1 , b=1 , ⇒2−1=1−2c ; c=0 ∴ f(x)=−x^2 +x { ((f(b)=f(1)=−1+1=0)),((f(a)=f(−1)=−1−1=−2)) :} ⇒ (1/2)[ f(b)−f(a) ]= (1/2)(0−(−2))=1](Q174119.png)
$${f}\left({ax}+{b}\right)={a}\left({ax}+{b}\right)^{\mathrm{2}} +{b}\left({ax}+{b}\right)+{c} \\ $$$${f}\left({bx}+{c}\right)={a}\left({bx}+{c}\right)^{\mathrm{2}} +{b}\left({bx}+{c}\right)+{c} \\ $$$$\begin{cases}{{f}\left({ax}+{b}\right)={a}^{\mathrm{3}} {x}^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{2}} {bx}+{ab}^{\mathrm{2}} +{abx}+{b}^{\mathrm{2}} +{c}}\\{{f}\left({bx}+{c}\right)={ab}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{2}{abcx}+{ac}^{\mathrm{2}} +{b}^{\mathrm{2}} {x}+{bc}+{c}}\end{cases} \\ $$$$\:\begin{cases}{{a}^{\mathrm{2}} ={b}^{\mathrm{2}} \Rightarrow\begin{cases}{{a}={b}\left({rejected}\right)}\\{{a}=−{b}}\end{cases}}\\{\mathrm{2}{a}^{\mathrm{2}} {b}+{ab}={b}^{\mathrm{2}} +\mathrm{2}{abc}}\\{{ab}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}={ac}^{\mathrm{2}} +{bc}+{c}}\end{cases} \\ $$$${for}\:{a}=−{b}\:\Rightarrow\begin{cases}{−\mathrm{2}{a}^{\mathrm{3}} −{a}^{\mathrm{2}} ={a}^{\mathrm{2}} −\mathrm{2}{a}^{\mathrm{2}} {c}}\\{{a}^{\mathrm{3}} +{a}^{\mathrm{2}} +{c}={ac}−{ac}+{c}}\end{cases} \\ $$$$\Rightarrow{a}^{\mathrm{2}} \left({a}+\mathrm{1}\right)=\mathrm{0}\Rightarrow{a}=−\mathrm{1}\:,\:{b}=\mathrm{1}\:,\: \\ $$$$\Rightarrow\mathrm{2}−\mathrm{1}=\mathrm{1}−\mathrm{2}{c}\:;\:{c}=\mathrm{0} \\ $$$$\therefore\:{f}\left({x}\right)=−{x}^{\mathrm{2}} +{x} \\ $$$$\begin{cases}{{f}\left({b}\right)={f}\left(\mathrm{1}\right)=−\mathrm{1}+\mathrm{1}=\mathrm{0}}\\{{f}\left({a}\right)={f}\left(−\mathrm{1}\right)=−\mathrm{1}−\mathrm{1}=−\mathrm{2}}\end{cases} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}\left[\:{f}\left({b}\right)−{f}\left({a}\right)\:\right]=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{0}−\left(−\mathrm{2}\right)\right)=\mathrm{1} \\ $$$$ \\ $$