
Question and Answers Forum
Question Number 174152 by cortano1 last updated on 26/Jul/22
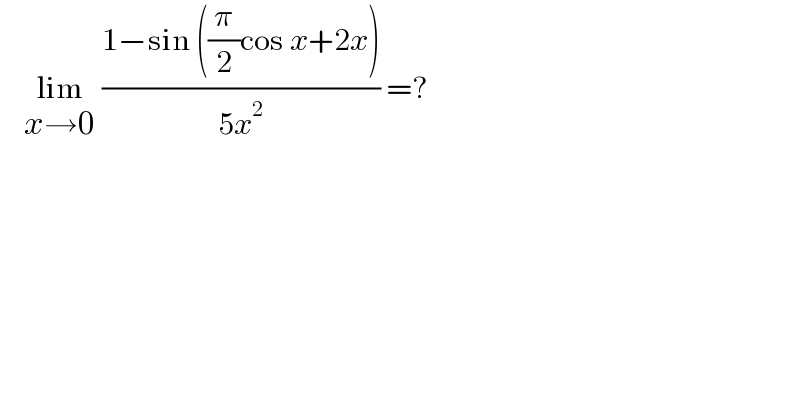
Answered by CElcedricjunior last updated on 26/Jul/22

Answered by a.lgnaoui last updated on 26/Jul/22
![sin ((π/2)cos x+2x)=sin ((π/2)cos x)cos 2x+cos ((π/2)cos x)sin 2x L=lim_(x→0) ((1−[sin ((π/2)cos x)cos 2x+cos ((π/2)cos x)sin 2x])/(5x^2 )) =lim_(x→0) [(1/(5x^2 ))−((((π/2)+2cos (π/2)sin x)/(5x^2 )))] lim_(x→0) [(1/(5x^2 ))−((π/2)/(5x^2 ))] ; lim_(x→0) ((sin x)/x)=1 L=lim_(x→0) (((2−π)/(10x^2 )))=−∞](Q174176.png)
| ||
Question and Answers Forum | ||
Question Number 174152 by cortano1 last updated on 26/Jul/22 | ||
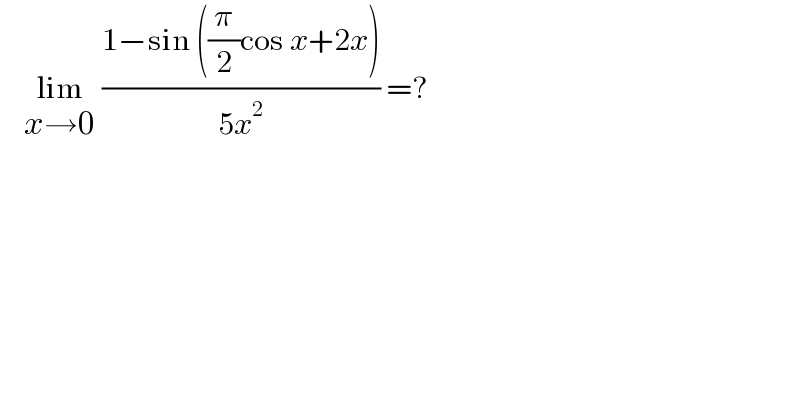 | ||
Answered by CElcedricjunior last updated on 26/Jul/22 | ||
 | ||
| ||
Answered by a.lgnaoui last updated on 26/Jul/22 | ||
![sin ((π/2)cos x+2x)=sin ((π/2)cos x)cos 2x+cos ((π/2)cos x)sin 2x L=lim_(x→0) ((1−[sin ((π/2)cos x)cos 2x+cos ((π/2)cos x)sin 2x])/(5x^2 )) =lim_(x→0) [(1/(5x^2 ))−((((π/2)+2cos (π/2)sin x)/(5x^2 )))] lim_(x→0) [(1/(5x^2 ))−((π/2)/(5x^2 ))] ; lim_(x→0) ((sin x)/x)=1 L=lim_(x→0) (((2−π)/(10x^2 )))=−∞](Q174176.png) | ||
| ||