
Question Number 174407 by infinityaction last updated on 31/Jul/22
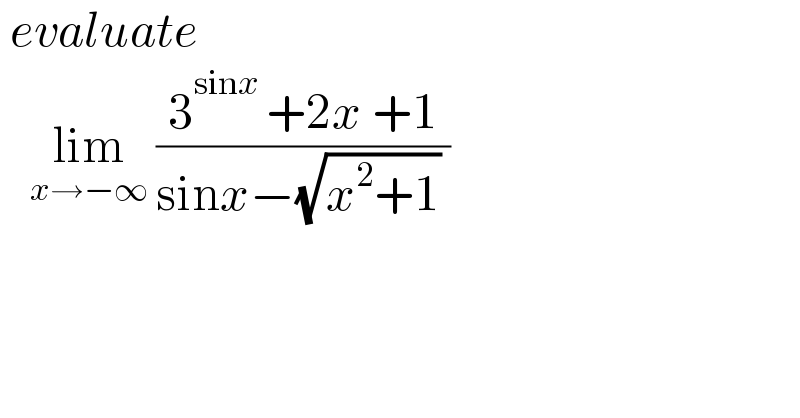
$$\:{evaluate} \\ $$$$\:\:\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\frac{\mathrm{3}^{\mathrm{sin}{x}\:} +\mathrm{2}{x}\:+\mathrm{1}}{\mathrm{sin}{x}−\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:} \\ $$
Answered by CElcedricjunior last updated on 31/Jul/22

$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\frac{\mathrm{3}^{\boldsymbol{{sinx}}} +\mathrm{2}\boldsymbol{{x}}+\mathrm{1}}{\boldsymbol{{sinx}}−\sqrt{\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\boldsymbol{{or}}\:\forall\boldsymbol{{x}}\in\mathbb{R}\:−\mathrm{1}\leqslant\boldsymbol{{sinx}}\leqslant\mathrm{1} \\ $$$$\Leftrightarrow\frac{\mathrm{1}}{\mathrm{3}}\leqslant\mathrm{3}^{\boldsymbol{{sinx}}} \leqslant\mathrm{3} \\ $$$$\Leftrightarrow\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{2}\boldsymbol{{x}}+\mathrm{1}\leqslant\mathrm{3}^{\boldsymbol{{sinx}}} +\mathrm{2}\boldsymbol{{x}}+\mathrm{1}\leqslant\mathrm{4}+\mathrm{2}\boldsymbol{{x}} \\ $$$$−\mathrm{1}\leqslant\boldsymbol{{sinx}}\leqslant\mathrm{1} \\ $$$$−\mathrm{1}−\sqrt{\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}}\leqslant\boldsymbol{{sinx}}−\sqrt{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} }\leqslant\mathrm{1}−\sqrt{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} } \\ $$$$\Leftrightarrow\frac{\frac{\mathrm{4}}{\mathrm{3}}+\mathrm{2}\boldsymbol{{x}}}{−\mathrm{1}−\sqrt{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} }}\leqslant\frac{\mathrm{3}^{\boldsymbol{{sinx}}} +\mathrm{2}\boldsymbol{{x}}+\mathrm{1}}{\boldsymbol{{sinx}}−\sqrt{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} }}\leqslant\frac{\mathrm{4}+\mathrm{2}\boldsymbol{{x}}}{\mathrm{1}−\sqrt{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} }} \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\frac{\frac{\mathrm{4}}{\mathrm{3}}+\mathrm{2}\boldsymbol{{x}}}{−\mathrm{1}−\sqrt{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} }}=\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\frac{\frac{\mathrm{4}}{\mathrm{3}}+\mathrm{2}{x}}{−\mathrm{1}−\mid\boldsymbol{{x}}\mid\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{2}} }}} \\ $$$$=\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\frac{\boldsymbol{{x}}\left(\frac{\mathrm{4}}{\mathrm{3}\boldsymbol{{x}}}+\mathrm{2}\right)}{\boldsymbol{{x}}\left(−\frac{\mathrm{1}}{\boldsymbol{{x}}}+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{2}} }}\right)}\:\boldsymbol{{cas}}\:\boldsymbol{{qd}}:\begin{cases}{\boldsymbol{{x}}−>−\infty}\\{\mid\boldsymbol{{x}}\mid=−\boldsymbol{{x}}}\end{cases} \\ $$$$=\mathrm{2} \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\frac{\mathrm{4}+\mathrm{2}\boldsymbol{{x}}}{\mathrm{1}−\sqrt{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} }}=\mathrm{2}\:\boldsymbol{{en}}\:\boldsymbol{{procedant}}\:\boldsymbol{{de}} \\ $$$$\boldsymbol{{la}}\:\boldsymbol{{meme}}\:\boldsymbol{{maniere}} \\ $$$$\boldsymbol{{d}}'\boldsymbol{\mathrm{o}}\grave {\boldsymbol{\mathrm{u}}}\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\frac{\mathrm{3}^{\boldsymbol{{sinx}}} +\mathrm{2}\boldsymbol{{x}}+\mathrm{1}}{\boldsymbol{{sinx}}−\sqrt{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} }}=\mathrm{2} \\ $$$$\mathscr{D}\:'{apr}\grave {{e}s}\:{le}\:{th}\acute {{e}or}\grave {{e}me}\:{des}\:{gendarmes} \\ $$$$ \\ $$$$.........{le}\:{c}\acute {{e}l}\grave {{e}bre}\:{cedric}\:{junior}........... \\ $$$$ \\ $$$$ \\ $$
Commented by infinityaction last updated on 01/Aug/22

$${thanks} \\ $$
