
Question and Answers Forum
Question Number 174439 by mnjuly1970 last updated on 01/Aug/22
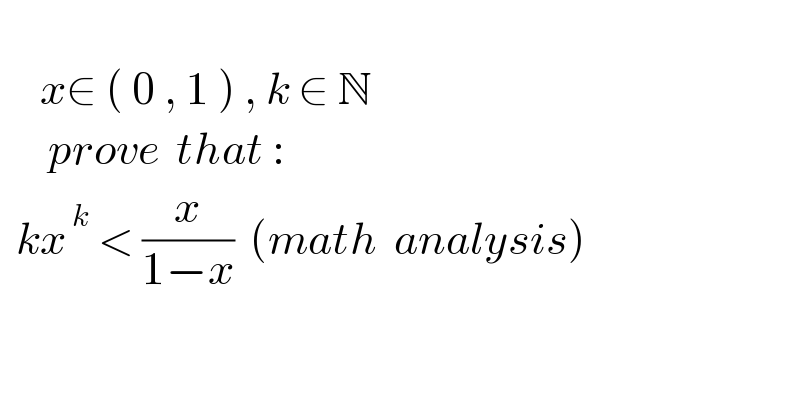
Answered by behi834171 last updated on 01/Aug/22
![for: k=1: 1×x^1 <^? (x/(1−x))⇒x<^? (x/(1−x)) 0<x<1⇒−1<−x<0⇒0<1−x<1 so: 1−x<1⇒(x/(1−x))>x , i.e:it is true for : k=1 let assume that is true for k=n we should prove that is true for k=n+1 (n+1)x^(n+1) <^? (x/(1−x)) (n+1)x^(n+1) (1−x)=(n+1)x^(n+1) −(n+1)x^(n+2) < <nx^n .x+x^(n+1) −nx^n .x^2 −x^(n+2) <(x/(1−x)).x−(x/(1−x)).x^2 +x^(n+1) −x^(n+2) = =((x^2 −x^3 )/(1−x))+x^(n+1) −x^(n+2) =x^2 +x^(n+1) −x^(n+2) < <x+x−x=x .hence proved. ■ [0<x<1⇒ x^(p∈N) <x]](Q174448.png)
| ||
Question and Answers Forum | ||
Question Number 174439 by mnjuly1970 last updated on 01/Aug/22 | ||
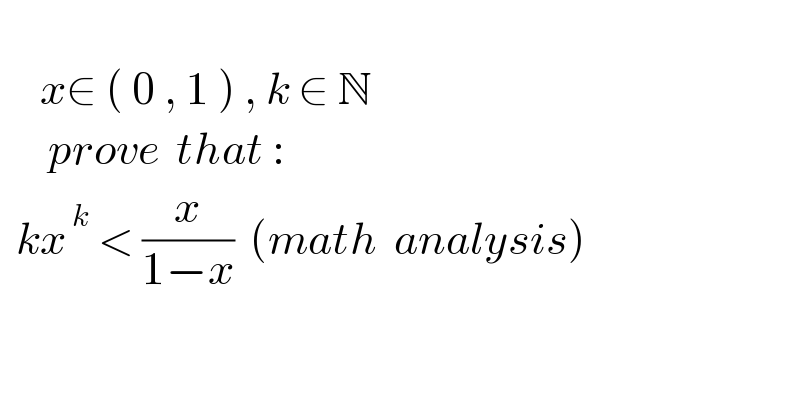 | ||
Answered by behi834171 last updated on 01/Aug/22 | ||
![for: k=1: 1×x^1 <^? (x/(1−x))⇒x<^? (x/(1−x)) 0<x<1⇒−1<−x<0⇒0<1−x<1 so: 1−x<1⇒(x/(1−x))>x , i.e:it is true for : k=1 let assume that is true for k=n we should prove that is true for k=n+1 (n+1)x^(n+1) <^? (x/(1−x)) (n+1)x^(n+1) (1−x)=(n+1)x^(n+1) −(n+1)x^(n+2) < <nx^n .x+x^(n+1) −nx^n .x^2 −x^(n+2) <(x/(1−x)).x−(x/(1−x)).x^2 +x^(n+1) −x^(n+2) = =((x^2 −x^3 )/(1−x))+x^(n+1) −x^(n+2) =x^2 +x^(n+1) −x^(n+2) < <x+x−x=x .hence proved. ■ [0<x<1⇒ x^(p∈N) <x]](Q174448.png) | ||
| ||