L(sin^n (x))=?


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 174508 by Gbenga last updated on 03/Aug/22

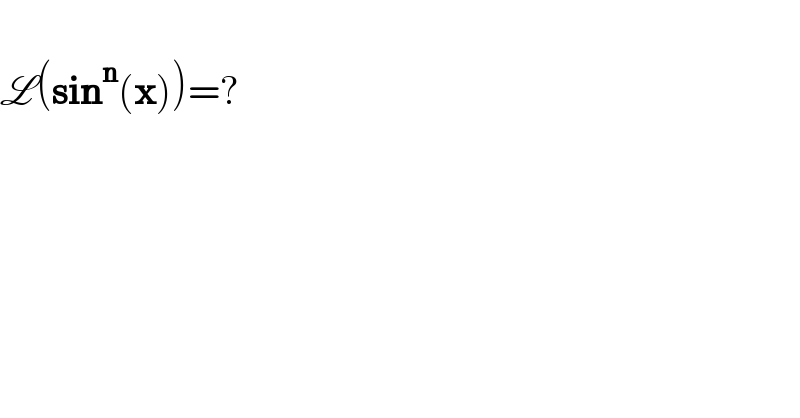
$L (\sin^{n} (x)) = ?$
	Answered by Mathspace last updated on 03/Aug/22
	$sin^n x=(((e^(ix) −e^(−ix) )/(2i)))^n =(1/((2i)^n ))Σ_(k=0) ^n C_n ^k (e^(ix) )^k (−e^(−ix) )^(n−k) =(1/((2i)^n ))Σ_(k=0) ^n C_n ^k (−1)^(n−k) e^(ikx−i(n−k)x) =(((−1)^n )/((2i)^n ))Σ_(k=0) ^n (−1)^k C_n ^k e^(i(2k−n)x) =(((−1)^n )/((2i)^n ))Σ_(k=0) ^n (−1)^k C_n ^k {cos(2k−n)x +isin(2k−n)x} ⇒L(sin^n x) =(((−1)^n )/((2i)^n ))Σ_(k=0) ^n (−1)^k C_n ^k L(cos(2k−n)x +i(((−1)^n )/((2i)^n ))Σ_(k=0) ^n (−1)^k C_n ^k L(sin(2k−n)x L(cos(2k−n)x) =∫_0 ^∞ cos(2k−n)t e^(−xt) dt =Re(∫_0 ^∞ e^(−xt+i(2k−n)t) dt) and ∫_0 ^∞ e^((−x+i(2k−n))t) dt =[(1/(−x+i(2k−n)))e^((−x+i(2k−n))t) ]_0 ^∞ =−(1/(−x+i(2k−n))) =(1/(x−i(2k−n)))=((x+i(2k−n))/(x^2 +(2k−n)^2 )) ⇒Re(....)=(x/(x^2 +(2k−n)^2 )) ⇒ L(sin^n x) =(((−1)^n )/((2i)^n ))Σ_(k=0) ^n (−1)^k C_n ^k (x/(x^2 +(2k−n)^2 )) +i(((−1)^n )/((2i)^n ))Σ_(k=0) ^n (−1)^k C_n ^k ((2k−n)/(x^2 +(2k−n)^2 ))$
	${s i n}^{n} x = {(\frac{e^{i x} - e^{- i x}}{2 i})}^{n}$ $= \frac{1}{{(2 i)}^{n}} \sum_{k = 0}^{n} C_{n}^{k} {(e^{i x})}^{k} {(- e^{- i x})}^{n - k}$ $= \frac{1}{{(2 i)}^{n}} \sum_{k = 0}^{n} C_{n}^{k} {(- 1)}^{n - k} e^{i k x - i (n - k) x}$ $= \frac{{(- 1)}^{n}}{{(2 i)}^{n}} \sum_{k = 0}^{n} {(- 1)}^{k} C_{n}^{k} e^{i (2 k - n) x}$ $= \frac{{(- 1)}^{n}}{{(2 i)}^{n}} \sum_{k = 0}^{n} {(- 1)}^{k} C_{n}^{k} {c o s (2 k - n) x + i s i n (2 k - n) x}$ $\Rightarrow L ({s i n}^{n} x)$ $= \frac{{(- 1)}^{n}}{{(2 i)}^{n}} \sum_{k = 0}^{n} {(- 1)}^{k} C_{n}^{k} L (c o s (2 k - n) x$ $+ i \frac{{(- 1)}^{n}}{{(2 i)}^{n}} \sum_{k = 0}^{n} {(- 1)}^{k} C_{n}^{k} L (s i n (2 k - n) x$ $L (c o s (2 k - n) x)$ $= \int_{0}^{\infty} c o s (2 k - n) t e^{- x t} d t$ $= R e (\int_{0}^{\infty} e^{- x t + i (2 k - n) t} d t)$ $a n d \int_{0}^{\infty} e^{(- x + i (2 k - n)) t} d t$ $= {[\frac{1}{- x + i (2 k - n)} e^{(- x + i (2 k - n)) t}]}_{0}^{\infty}$ $= - \frac{1}{- x + i (2 k - n)}$ $= \frac{1}{x - i (2 k - n)} = \frac{x + i (2 k - n)}{x^{2} + {(2 k - n)}^{2}}$ $\Rightarrow R e (. . . .) = \frac{x}{x^{2} + {(2 k - n)}^{2}} \Rightarrow$ $L ({s i n}^{n} x)$ $= \frac{{(- 1)}^{n}}{{(2 i)}^{n}} \sum_{k = 0}^{n} {(- 1)}^{k} C_{n}^{k} \frac{x}{x^{2} + {(2 k - n)}^{2}}$ $+ i \frac{{(- 1)}^{n}}{{(2 i)}^{n}} \sum_{k = 0}^{n} {(- 1)}^{k} C_{n}^{k} \frac{2 k - n}{x^{2} + {(2 k - n)}^{2}}$
	Commented by Gbenga last updated on 03/Aug/22

	$t h a n k s s k$
	Commented by Tawa11 last updated on 03/Aug/22

	$Great sir$
	Commented by Mathspace last updated on 03/Aug/22

	$t h a n k s$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum