Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 174514 by Best1 last updated on 03/Aug/22

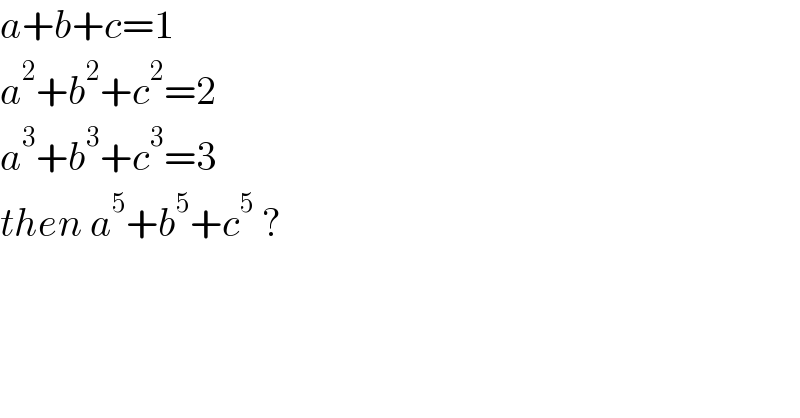
a+b+c=1 a^2 +b^2 +c^2 =2 a^3 +b^3 +c^3 =3 then a^5 +b^5 +c^5 ?

$${a}+{b}+{c}=\mathrm{1} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{2} \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} =\mathrm{3} \\ $$$${then}\:{a}^{\mathrm{5}} +{b}^{\mathrm{5}} +{c}^{\mathrm{5}} \:? \\ $$

Commented by mr W last updated on 03/Aug/22

see Q74970

$${see}\:{Q}\mathrm{74970} \\ $$

Answered by RedMath last updated on 03/Aug/22

no idea lol

$${no}\:{idea}\:{lol} \\ $$

Commented by Best1 last updated on 03/Aug/22

sorry

$${sorry} \\ $$

Answered by MJS_new last updated on 03/Aug/22

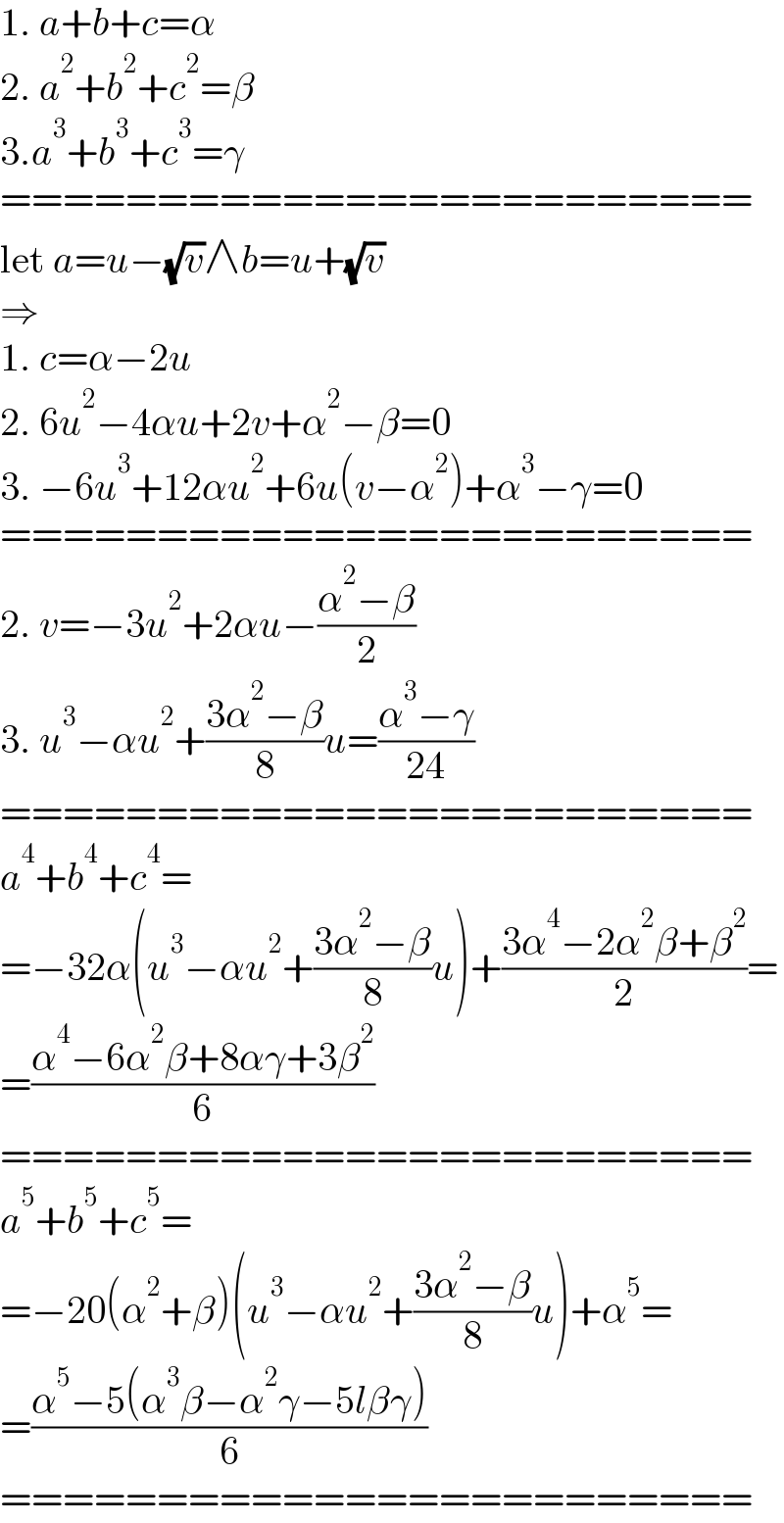
1. a+b+c=α 2. a^2 +b^2 +c^2 =β 3.a^3 +b^3 +c^3 =γ ======================== let a=u−(√v)∧b=u+(√v) ⇒ 1. c=α−2u 2. 6u^2 −4αu+2v+α^2 −β=0 3. −6u^3 +12αu^2 +6u(v−α^2 )+α^3 −γ=0 ======================== 2. v=−3u^2 +2αu−((α^2 −β)/2) 3. u^3 −αu^2 +((3α^2 −β)/8)u=((α^3 −γ)/(24)) ======================== a^4 +b^4 +c^4 = =−32α(u^3 −αu^2 +((3α^2 −β)/8)u)+((3α^4 −2α^2 β+β^2 )/2)= =((α^4 −6α^2 β+8αγ+3β^2 )/6) ======================== a^5 +b^5 +c^5 = =−20(α^2 +β)(u^3 −αu^2 +((3α^2 −β)/8)u)+α^5 = =((α^5 −5(α^3 β−α^2 γ−5lβγ))/6) ========================

$$\mathrm{1}.\:{a}+{b}+{c}=\alpha \\ $$$$\mathrm{2}.\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\beta \\ $$$$\mathrm{3}.{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} =\gamma \\ $$$$======================== \\ $$$$\mathrm{let}\:{a}={u}−\sqrt{{v}}\wedge{b}={u}+\sqrt{{v}} \\ $$$$\Rightarrow \\ $$$$\mathrm{1}.\:{c}=\alpha−\mathrm{2}{u} \\ $$$$\mathrm{2}.\:\mathrm{6}{u}^{\mathrm{2}} −\mathrm{4}\alpha{u}+\mathrm{2}{v}+\alpha^{\mathrm{2}} −\beta=\mathrm{0} \\ $$$$\mathrm{3}.\:−\mathrm{6}{u}^{\mathrm{3}} +\mathrm{12}\alpha{u}^{\mathrm{2}} +\mathrm{6}{u}\left({v}−\alpha^{\mathrm{2}} \right)+\alpha^{\mathrm{3}} −\gamma=\mathrm{0} \\ $$$$======================== \\ $$$$\mathrm{2}.\:{v}=−\mathrm{3}{u}^{\mathrm{2}} +\mathrm{2}\alpha{u}−\frac{\alpha^{\mathrm{2}} −\beta}{\mathrm{2}} \\ $$$$\mathrm{3}.\:{u}^{\mathrm{3}} −\alpha{u}^{\mathrm{2}} +\frac{\mathrm{3}\alpha^{\mathrm{2}} −\beta}{\mathrm{8}}{u}=\frac{\alpha^{\mathrm{3}} −\gamma}{\mathrm{24}} \\ $$$$======================== \\ $$$${a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} = \\ $$$$=−\mathrm{32}\alpha\left({u}^{\mathrm{3}} −\alpha{u}^{\mathrm{2}} +\frac{\mathrm{3}\alpha^{\mathrm{2}} −\beta}{\mathrm{8}}{u}\right)+\frac{\mathrm{3}\alpha^{\mathrm{4}} −\mathrm{2}\alpha^{\mathrm{2}} \beta+\beta^{\mathrm{2}} }{\mathrm{2}}= \\ $$$$=\frac{\alpha^{\mathrm{4}} −\mathrm{6}\alpha^{\mathrm{2}} \beta+\mathrm{8}\alpha\gamma+\mathrm{3}\beta^{\mathrm{2}} }{\mathrm{6}} \\ $$$$======================== \\ $$$${a}^{\mathrm{5}} +{b}^{\mathrm{5}} +{c}^{\mathrm{5}} = \\ $$$$=−\mathrm{20}\left(\alpha^{\mathrm{2}} +\beta\right)\left({u}^{\mathrm{3}} −\alpha{u}^{\mathrm{2}} +\frac{\mathrm{3}\alpha^{\mathrm{2}} −\beta}{\mathrm{8}}{u}\right)+\alpha^{\mathrm{5}} = \\ $$$$=\frac{\alpha^{\mathrm{5}} −\mathrm{5}\left(\alpha^{\mathrm{3}} \beta−\alpha^{\mathrm{2}} \gamma−\mathrm{5}{l}\beta\gamma\right)}{\mathrm{6}} \\ $$$$======================== \\ $$

Commented by Tawa11 last updated on 03/Aug/22

Great sirs.

$$\mathrm{Great}\:\mathrm{sirs}. \\ $$

Answered by behi834171 last updated on 03/Aug/22

a^2 +ab+ac=a ab+b^2 +bc=b ac+bc+c^2 =c⇒2Σab=Σa−Σa^2 =1−2=−1 ⇒Σab=−(1/2) a^3 +a(b^2 +c^2 )=2a b(a^2 +c^2 )+b^3 =2b c(a^2 +b^2 )+c^3 =2c⇒ ⇒Σab(a+b)=2Σa−Σa^3 =2−3=−1 ⇒Σab(1−c)=−1⇒Σab−3abc=−1 ⇒−3abc=−1+(1/2)=−(1/2)⇒abc=(1/6) so:a,b,c, are the roots of equation: z^3 −z^2 −(1/2)z−(1/6)=0 z^5 =z^3 .z^2 =z^2 (z^2 +(1/2)z+(1/6))=z^4 +(1/2)z^3 +(1/6)z^2 = =z(z^2 +(1/2)z+(1/6))+(1/2)(z^2 +(1/2)z+(1/6))+(1/6)z^2 = =z^2 +(1/2)z+(1/6)+(1/2)z^2 +(1/6)z+(1/2)z^2 +(1/4)z+(1/(12))+(1/6)z^2 = =((13)/6)z^2 +((11)/(12))z+(1/4) ⇒Σa^5 =((13)/6)Σa^2 +((11)/(12))Σa+(3/4)= =((13)/6)×2+((11)/(12))×1+(3/4)=6 .■ ...................................... by using symbols of dear mr:MJS_new Σab=((Σa−Σa^2 )/2)=((𝛂−𝛃)/2) Σab−3abc=2Σa−Σa^3 ⇒ abc=−(1/3)(2𝛂−𝛄−((𝛂−𝛃)/2))=−((3𝛂+𝛃−2𝛄)/6) ⇒z^3 −𝛂z^2 +((𝛂−𝛃)/2)z+((3𝛂+𝛃−2𝛄)/6)=0 ⇒z^5 =z^2 z^3 =z^2 (𝛂z^2 −((𝛂−𝛃)/2)z−((3𝛂+𝛃−2𝛄)/6))= =𝛂z(𝛂z^2 −((𝛂−𝛃)/2)z−((3𝛂+𝛃−2𝛄)/6))−((𝛂−𝛃)/2)(𝛂z^2 −((𝛂−𝛃)/2)z−((3𝛂+𝛃−2𝛄)/6))−((3𝛂+𝛃−2𝛄)/6)z^2 = =𝛂^2 (𝛂z^2 −((𝛂−𝛃)/2)z−((3𝛂+𝛃−2𝛄)/6))−((𝛂(𝛂−𝛃))/2)z^2 −((𝛂(3𝛂+𝛃−2𝛄))/6)z− +((𝛂(𝛂−𝛃))/2)z^2 +(((𝛂−𝛃)^2 )/4)z+(((𝛂−𝛃)(3𝛂+𝛃−2𝛄))/(12))−((3𝛂+𝛃−2𝛄)/6)z^2 = =[𝛂^3 −((𝛂(𝛂−𝛃))/2)−((3𝛂+𝛃−2𝛄)/6)]z^2 −[((𝛂^2 (𝛂−𝛃))/2)+((𝛂(3𝛂+𝛃−2𝛄))/6)−(((𝛂−𝛃)^2 )/4)].z− −(((2𝛂^2 −𝛂+𝛃)(3𝛂+𝛃−2𝛄))/(12)) =A.z^2 +B.z+C A=((6𝛂^3 −3𝛂^2 +3𝛂𝛃−3𝛂−𝛃+2𝛄)/6) B=−((6𝛂^3 −6𝛂^2 𝛃+3𝛂^2 +8𝛂𝛃−4𝛂𝛄−3𝛃^2 )/(12)) C=−((6𝛂^3 +2𝛂^2 𝛃−4𝛂^2 𝛄−3𝛂^2 +2𝛂𝛃+2𝛂𝛄+𝛃^2 −2𝛃𝛄)/(12)) ⇒Σa^5 =A.Σa^2 +B.Σa+3C

$${a}^{\mathrm{2}} +{ab}+{ac}={a} \\ $$$${ab}+{b}^{\mathrm{2}} +{bc}={b} \\ $$$${ac}+{bc}+{c}^{\mathrm{2}} ={c}\Rightarrow\mathrm{2}\Sigma{ab}=\Sigma{a}−\Sigma{a}^{\mathrm{2}} =\mathrm{1}−\mathrm{2}=−\mathrm{1} \\ $$$$\Rightarrow\Sigma{ab}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${a}^{\mathrm{3}} +{a}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)=\mathrm{2}{a} \\ $$$${b}\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)+{b}^{\mathrm{3}} =\mathrm{2}{b} \\ $$$${c}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)+{c}^{\mathrm{3}} =\mathrm{2}{c}\Rightarrow \\ $$$$\Rightarrow\Sigma{ab}\left({a}+{b}\right)=\mathrm{2}\Sigma{a}−\Sigma{a}^{\mathrm{3}} =\mathrm{2}−\mathrm{3}=−\mathrm{1} \\ $$$$\Rightarrow\Sigma{ab}\left(\mathrm{1}−{c}\right)=−\mathrm{1}\Rightarrow\Sigma{ab}−\mathrm{3}{abc}=−\mathrm{1} \\ $$$$\Rightarrow−\mathrm{3}{abc}=−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}=−\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\boldsymbol{{abc}}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\boldsymbol{{so}}:\boldsymbol{{a}},\boldsymbol{{b}},\boldsymbol{{c}},\:{are}\:{the}\:{roots}\:{of}\:{equation}: \\ $$$$\:\:\:\:\:\boldsymbol{{z}}^{\mathrm{3}} −\boldsymbol{{z}}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{z}}−\frac{\mathrm{1}}{\mathrm{6}}=\mathrm{0} \\ $$$$\boldsymbol{{z}}^{\mathrm{5}} =\boldsymbol{{z}}^{\mathrm{3}} .\boldsymbol{{z}}^{\mathrm{2}} =\boldsymbol{{z}}^{\mathrm{2}} \left(\boldsymbol{{z}}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{z}}+\frac{\mathrm{1}}{\mathrm{6}}\right)=\boldsymbol{{z}}^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{z}}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{6}}\boldsymbol{{z}}^{\mathrm{2}} = \\ $$$$=\boldsymbol{{z}}\left(\boldsymbol{{z}}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{z}}+\frac{\mathrm{1}}{\mathrm{6}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\boldsymbol{{z}}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{z}}+\frac{\mathrm{1}}{\mathrm{6}}\right)+\frac{\mathrm{1}}{\mathrm{6}}\boldsymbol{{z}}^{\mathrm{2}} = \\ $$$$=\boldsymbol{{z}}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{z}}+\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{2}}{z}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{6}}{z}+\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{z}}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}{z}+\frac{\mathrm{1}}{\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{6}}\boldsymbol{{z}}^{\mathrm{2}} = \\ $$$$=\frac{\mathrm{13}}{\mathrm{6}}\boldsymbol{{z}}^{\mathrm{2}} +\frac{\mathrm{11}}{\mathrm{12}}\boldsymbol{{z}}+\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\Sigma\boldsymbol{{a}}^{\mathrm{5}} =\frac{\mathrm{13}}{\mathrm{6}}\Sigma\boldsymbol{{a}}^{\mathrm{2}} +\frac{\mathrm{11}}{\mathrm{12}}\Sigma\boldsymbol{{a}}+\frac{\mathrm{3}}{\mathrm{4}}= \\ $$$$=\frac{\mathrm{13}}{\mathrm{6}}×\mathrm{2}+\frac{\mathrm{11}}{\mathrm{12}}×\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}=\mathrm{6}\:\:\:\:.\blacksquare \\ $$$$...................................... \\ $$$${by}\:{using}\:{symbols}\:{of}\:{dear}\:{mr}:{MJS\_new} \\ $$$$\Sigma\boldsymbol{{ab}}=\frac{\Sigma\boldsymbol{{a}}−\Sigma\boldsymbol{{a}}^{\mathrm{2}} }{\mathrm{2}}=\frac{\boldsymbol{\alpha}−\boldsymbol{\beta}}{\mathrm{2}} \\ $$$$\Sigma\boldsymbol{{ab}}−\mathrm{3}\boldsymbol{{abc}}=\mathrm{2}\Sigma\boldsymbol{{a}}−\Sigma\boldsymbol{{a}}^{\mathrm{3}} \Rightarrow \\ $$$$\boldsymbol{{abc}}=−\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}\boldsymbol{\alpha}−\boldsymbol{\gamma}−\frac{\boldsymbol{\alpha}−\boldsymbol{\beta}}{\mathrm{2}}\right)=−\frac{\mathrm{3}\boldsymbol{\alpha}+\boldsymbol{\beta}−\mathrm{2}\boldsymbol{\gamma}}{\mathrm{6}} \\ $$$$\Rightarrow\boldsymbol{{z}}^{\mathrm{3}} −\boldsymbol{\alpha{z}}^{\mathrm{2}} +\frac{\boldsymbol{\alpha}−\boldsymbol{\beta}}{\mathrm{2}}\boldsymbol{{z}}+\frac{\mathrm{3}\boldsymbol{\alpha}+\boldsymbol{\beta}−\mathrm{2}\boldsymbol{\gamma}}{\mathrm{6}}=\mathrm{0} \\ $$$$\Rightarrow\boldsymbol{{z}}^{\mathrm{5}} =\boldsymbol{{z}}^{\mathrm{2}} \boldsymbol{{z}}^{\mathrm{3}} =\boldsymbol{{z}}^{\mathrm{2}} \left(\boldsymbol{\alpha{z}}^{\mathrm{2}} −\frac{\boldsymbol{\alpha}−\boldsymbol{\beta}}{\mathrm{2}}\boldsymbol{{z}}−\frac{\mathrm{3}\boldsymbol{\alpha}+\boldsymbol{\beta}−\mathrm{2}\boldsymbol{\gamma}}{\mathrm{6}}\right)= \\ $$$$=\boldsymbol{\alpha{z}}\left(\boldsymbol{\alpha{z}}^{\mathrm{2}} −\frac{\boldsymbol{\alpha}−\boldsymbol{\beta}}{\mathrm{2}}\boldsymbol{{z}}−\frac{\mathrm{3}\boldsymbol{\alpha}+\boldsymbol{\beta}−\mathrm{2}\boldsymbol{\gamma}}{\mathrm{6}}\right)−\frac{\boldsymbol{\alpha}−\boldsymbol{\beta}}{\mathrm{2}}\left(\boldsymbol{\alpha{z}}^{\mathrm{2}} −\frac{\boldsymbol{\alpha}−\boldsymbol{\beta}}{\mathrm{2}}\boldsymbol{{z}}−\frac{\mathrm{3}\boldsymbol{\alpha}+\boldsymbol{\beta}−\mathrm{2}\boldsymbol{\gamma}}{\mathrm{6}}\right)−\frac{\mathrm{3}\boldsymbol{\alpha}+\boldsymbol{\beta}−\mathrm{2}\boldsymbol{\gamma}}{\mathrm{6}}\boldsymbol{{z}}^{\mathrm{2}} = \\ $$$$=\boldsymbol{\alpha}^{\mathrm{2}} \left(\boldsymbol{\alpha{z}}^{\mathrm{2}} −\frac{\boldsymbol{\alpha}−\boldsymbol{\beta}}{\mathrm{2}}\boldsymbol{{z}}−\frac{\mathrm{3}\boldsymbol{\alpha}+\boldsymbol{\beta}−\mathrm{2}\boldsymbol{\gamma}}{\mathrm{6}}\right)−\frac{\boldsymbol{\alpha}\left(\boldsymbol{\alpha}−\boldsymbol{\beta}\right)}{\mathrm{2}}\boldsymbol{{z}}^{\mathrm{2}} −\frac{\boldsymbol{\alpha}\left(\mathrm{3}\boldsymbol{\alpha}+\boldsymbol{\beta}−\mathrm{2}\boldsymbol{\gamma}\right)}{\mathrm{6}}\boldsymbol{{z}}− \\ $$$$+\frac{\boldsymbol{\alpha}\left(\boldsymbol{\alpha}−\boldsymbol{\beta}\right)}{\mathrm{2}}\boldsymbol{{z}}^{\mathrm{2}} +\frac{\left(\boldsymbol{\alpha}−\boldsymbol{\beta}\right)^{\mathrm{2}} }{\mathrm{4}}\boldsymbol{{z}}+\frac{\left(\boldsymbol{\alpha}−\boldsymbol{\beta}\right)\left(\mathrm{3}\boldsymbol{\alpha}+\boldsymbol{\beta}−\mathrm{2}\boldsymbol{\gamma}\right)}{\mathrm{12}}−\frac{\mathrm{3}\boldsymbol{\alpha}+\boldsymbol{\beta}−\mathrm{2}\boldsymbol{\gamma}}{\mathrm{6}}\boldsymbol{{z}}^{\mathrm{2}} = \\ $$$$=\left[\boldsymbol{\alpha}^{\mathrm{3}} −\frac{\boldsymbol{\alpha}\left(\boldsymbol{\alpha}−\boldsymbol{\beta}\right)}{\mathrm{2}}−\frac{\mathrm{3}\boldsymbol{\alpha}+\boldsymbol{\beta}−\mathrm{2}\boldsymbol{\gamma}}{\mathrm{6}}\right]\boldsymbol{{z}}^{\mathrm{2}} −\left[\frac{\boldsymbol{\alpha}^{\mathrm{2}} \left(\boldsymbol{\alpha}−\boldsymbol{\beta}\right)}{\mathrm{2}}+\frac{\boldsymbol{\alpha}\left(\mathrm{3}\boldsymbol{\alpha}+\boldsymbol{\beta}−\mathrm{2}\boldsymbol{\gamma}\right)}{\mathrm{6}}−\frac{\left(\boldsymbol{\alpha}−\boldsymbol{\beta}\right)^{\mathrm{2}} }{\mathrm{4}}\right].\boldsymbol{{z}}− \\ $$$$−\frac{\left(\mathrm{2}\boldsymbol{\alpha}^{\mathrm{2}} −\boldsymbol{\alpha}+\boldsymbol{\beta}\right)\left(\mathrm{3}\boldsymbol{\alpha}+\boldsymbol{\beta}−\mathrm{2}\boldsymbol{\gamma}\right)}{\mathrm{12}} \\ $$$$=\boldsymbol{{A}}.\boldsymbol{{z}}^{\mathrm{2}} +\boldsymbol{{B}}.\boldsymbol{{z}}+\boldsymbol{{C}} \\ $$$$\boldsymbol{{A}}=\frac{\mathrm{6}\boldsymbol{\alpha}^{\mathrm{3}} −\mathrm{3}\boldsymbol{\alpha}^{\mathrm{2}} +\mathrm{3}\boldsymbol{\alpha\beta}−\mathrm{3}\boldsymbol{\alpha}−\boldsymbol{\beta}+\mathrm{2}\boldsymbol{\gamma}}{\mathrm{6}} \\ $$$$\boldsymbol{{B}}=−\frac{\mathrm{6}\boldsymbol{\alpha}^{\mathrm{3}} −\mathrm{6}\boldsymbol{\alpha}^{\mathrm{2}} \boldsymbol{\beta}+\mathrm{3}\boldsymbol{\alpha}^{\mathrm{2}} +\mathrm{8}\boldsymbol{\alpha\beta}−\mathrm{4}\boldsymbol{\alpha\gamma}−\mathrm{3}\boldsymbol{\beta}^{\mathrm{2}} }{\mathrm{12}} \\ $$$$\boldsymbol{{C}}=−\frac{\mathrm{6}\boldsymbol{\alpha}^{\mathrm{3}} +\mathrm{2}\boldsymbol{\alpha}^{\mathrm{2}} \boldsymbol{\beta}−\mathrm{4}\boldsymbol{\alpha}^{\mathrm{2}} \boldsymbol{\gamma}−\mathrm{3}\boldsymbol{\alpha}^{\mathrm{2}} +\mathrm{2}\boldsymbol{\alpha\beta}+\mathrm{2}\boldsymbol{\alpha\gamma}+\boldsymbol{\beta}^{\mathrm{2}} −\mathrm{2}\boldsymbol{\beta\gamma}}{\mathrm{12}} \\ $$$$\Rightarrow\Sigma\boldsymbol{{a}}^{\mathrm{5}} =\boldsymbol{{A}}.\Sigma\boldsymbol{{a}}^{\mathrm{2}} +\boldsymbol{{B}}.\Sigma\boldsymbol{{a}}+\mathrm{3}\boldsymbol{{C}} \\ $$

Commented by Best1 last updated on 03/Aug/22

wawww thanks guys

$$ \\ $$$${wawww}\:{thanks}\:{guys} \\ $$

Commented by Tawa11 last updated on 03/Aug/22

Great sirs

$$\mathrm{Great}\:\mathrm{sirs} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com