
Question and Answers Forum
Question Number 174728 by ajfour last updated on 09/Aug/22

Commented by ajfour last updated on 09/Aug/22

Commented by mr W last updated on 14/Aug/22
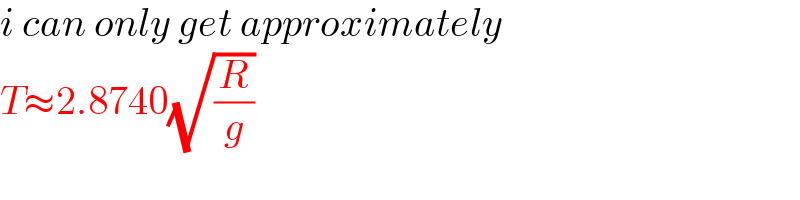
Commented by ajfour last updated on 14/Aug/22

Answered by mr W last updated on 13/Aug/22

Commented by mr W last updated on 15/Aug/22
![AB=L=4R AC=a−Rθ I_C =((L^2 m)/(12))+((L/2)−a+Rθ)^2 m let b=(L/2)−a I_C =((L^2 m)/(12))+(b+Rθ)^2 m y_M =R sin θ−(b+Rθ)cos θ ((I_C ω^2 )/2)=mg(((4R)/3)−R sin θ+(b+Rθ)cos θ) (ω^2 /2)[((L^2 m)/(12))+(b+Rθ)^2 m]=mg(((4R)/3)−R sin θ+(b+Rθ)cos θ) ω^2 [(4/3)+((b/R)+θ)^2 ]=((2g)/R)[(4/3)−sin θ+((b/R)+θ)cos θ] ω=−(dθ/dt)=(√((2g)/R))(√(((4/3)−sin θ+((b/R)+θ)cos θ)/((4/3)+((b/R)+θ)^2 ))) ∫_0 ^T dt=(√(R/(2g)))∫_θ_1 ^θ_0 (√(((4/3)+((b/R)+θ)^2 )/((4/3)−sin θ+((b/R)+θ)cos θ))) dθ T=(√(R/(2g)))∫_θ_1 ^θ_0 (√(((4/3)+((b/R)+θ)^2 )/((4/3)−sin θ+((b/R)+θ)cos θ))) dθ T=(√(R/(2g)))∫_θ_1 ^θ_0 (√(((4/3)+[θ−(((π+(√5))/2)+sin^(−1) (2/3)−2)]^2 )/((4/3)−sin θ+[θ−(((π+(√5))/2)+sin^(−1) (2/3)−2)]cos θ))) dθ T=(√(R/(2g)))∫_(1.0097) ^(2.3005) (√(((4/3)+(θ−1.418558)^2 )/((4/3)−sin θ+(θ−1.418558)cos θ))) dθ T≈2.8740(√(R/g))](Q174916.png)
Commented by ajfour last updated on 14/Aug/22
![let centre of semicircle be O. L=2l I_0 =I_m +m{r^2 +(a−rθ)^2 } I_m =((ml^2 )/3) mg{rcos θ+[l−(a−rθ)]sin θ}dt =d{I_0 ((dθ/dt))} g{rcos θ+(l+rθ−a)sin θ}dθ =((dθ/dt))d{[(l^2 /3)+r^2 +(a−rθ)^2 ]((dθ/dt))} here l=2r , a=((√5)/2)r ((g/r)){cos θ+(θ+2−((√5)/2))sin θ}dθ =ωd{[(7/3)+(((√5)/2)−θ)^2 ]ω} MjS sir may let us know with some great calculator θ(t). Given (g/r)=c, boundary value θ=sin^(−1) (2/3) for ω=0.](Q174918.png)
Commented by mr W last updated on 14/Aug/22

Commented by mr W last updated on 14/Aug/22
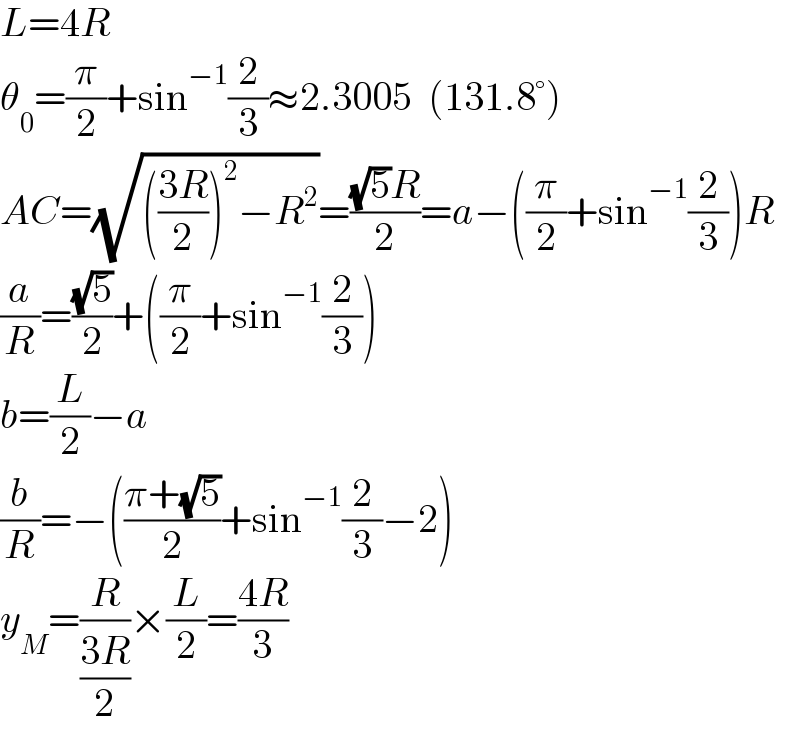
Commented by mr W last updated on 14/Aug/22

Commented by mr W last updated on 14/Aug/22

