
Question and Answers Forum
Question Number 174883 by infinityaction last updated on 13/Aug/22
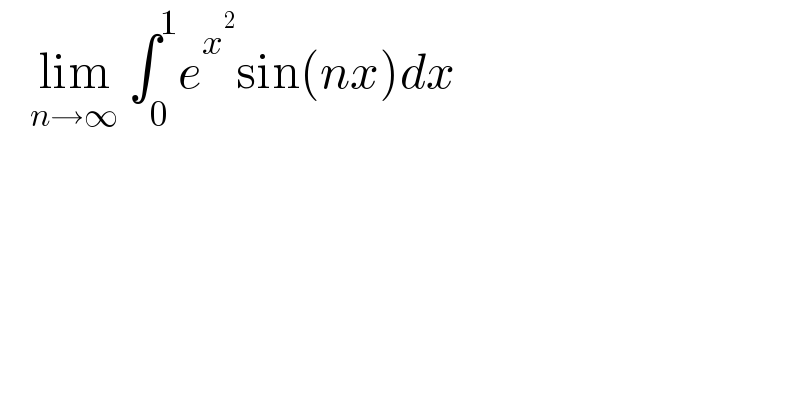
Answered by Mathspace last updated on 14/Aug/22
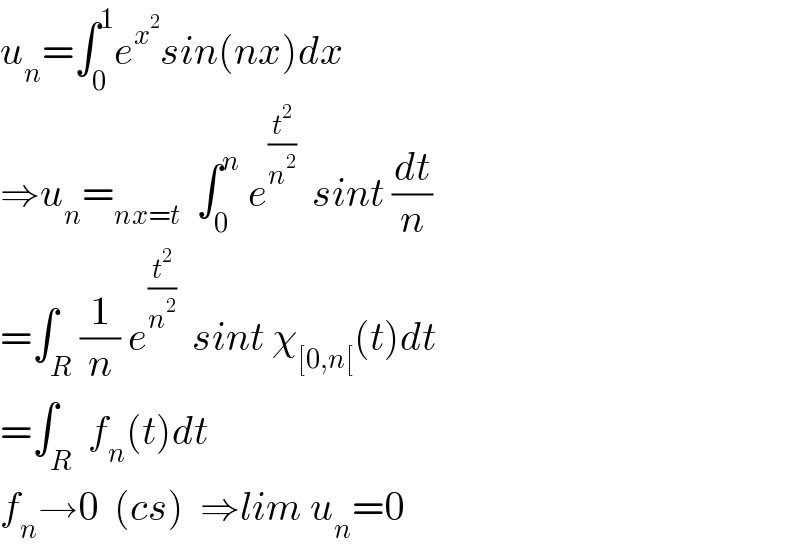
Answered by Mathspace last updated on 14/Aug/22
![another way by ρarts u_n =[−(1/n)cos(nx)e^x^2 ]_0 ^1 +(1/n)∫_0 ^1 e^x^2 cos(nx)dx (1/n)−e((cosn)/n) +(1/n)∫_0 ^1 e^x^2 cos(nx)dx ∣u_n ∣≤(1/n)+(e/n) +(1/n)∫_0 ^1 e^x^2 dx→0(n→+∞) ⇒lim u_n =0](Q174913.png)
Commented by infinityaction last updated on 14/Aug/22

| ||
Question and Answers Forum | ||
Question Number 174883 by infinityaction last updated on 13/Aug/22 | ||
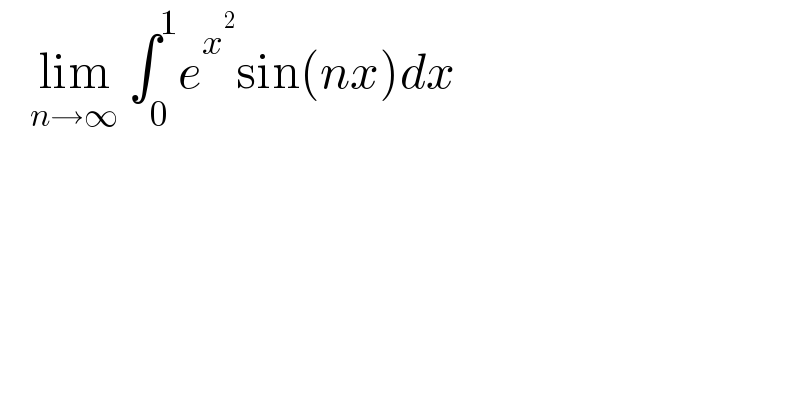 | ||
Answered by Mathspace last updated on 14/Aug/22 | ||
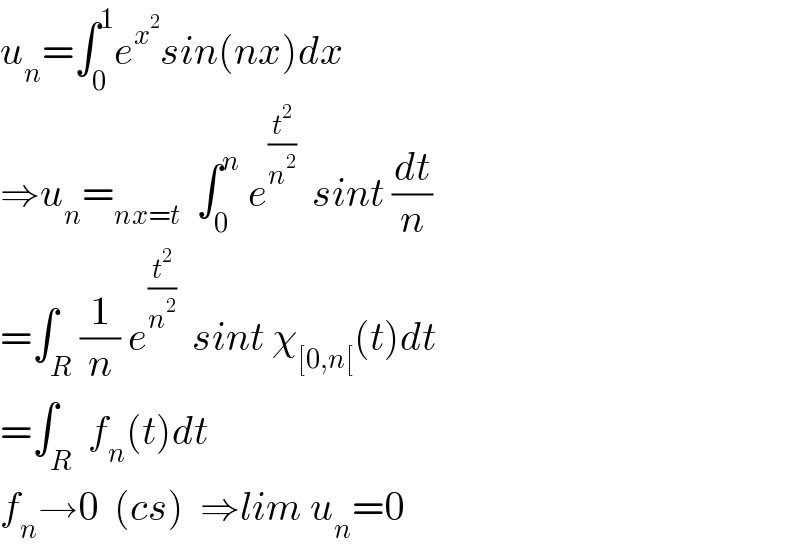 | ||
| ||
Answered by Mathspace last updated on 14/Aug/22 | ||
![another way by ρarts u_n =[−(1/n)cos(nx)e^x^2 ]_0 ^1 +(1/n)∫_0 ^1 e^x^2 cos(nx)dx (1/n)−e((cosn)/n) +(1/n)∫_0 ^1 e^x^2 cos(nx)dx ∣u_n ∣≤(1/n)+(e/n) +(1/n)∫_0 ^1 e^x^2 dx→0(n→+∞) ⇒lim u_n =0](Q174913.png) | ||
| ||
Commented by infinityaction last updated on 14/Aug/22 | ||
 | ||