Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 174982 by MikeH last updated on 15/Aug/22

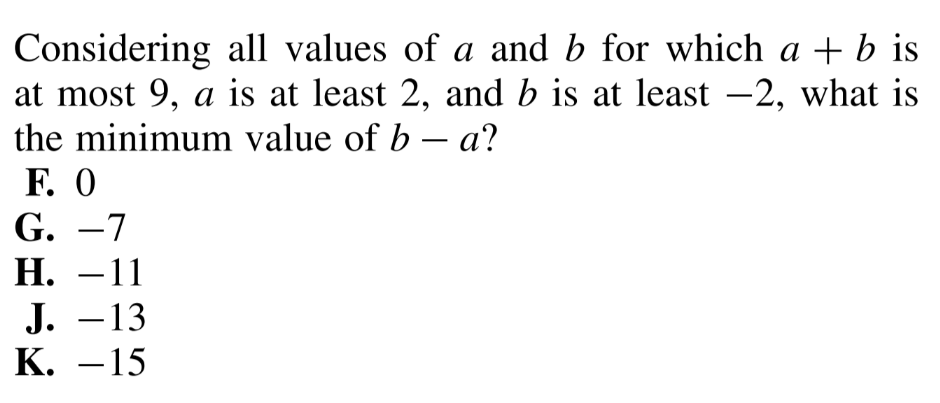
Answered by Rasheed.Sindhi last updated on 15/Aug/22

$$a+b⩽9\wedge \underset{\left(i\right)}{\underbrace{a⩾2}}\wedge \underset{\left(ii\right)}{\underbrace{b⩾-2}}$$$$\left(ii\right)-\left(i\right)\Rightarrow b-a⩾-2-2=-4$$$$Minimumvalueofb-ais-4$$

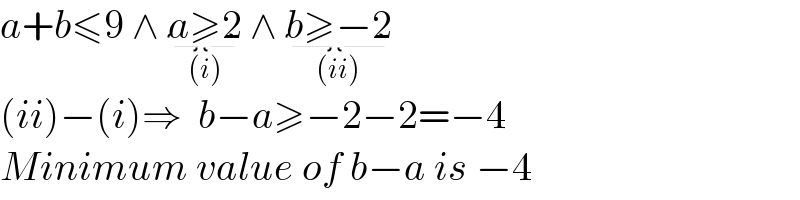
Commented by JDamian last updated on 15/Aug/22

that is not correct, sir. if a=3 and b=-2, then b-a = -5

Commented by MikeH last updated on 15/Aug/22

$$\mathrm{I}\mathrm{got}\mathrm{an}\mathrm{answer}\mathrm{which}{\mathrm{I}}^{\prime }\mathrm{m}\mathrm{not}\mathrm{sure}\mathrm{of}$$$${\mathrm{that}}^{\prime }\mathrm{s}\mathrm{why}\mathrm{I}\mathrm{posted}.\mathrm{it}\mathrm{goes}\mathrm{as}\mathrm{follows}$$$$$$$$a+b⩽9\mathrm{and}a⩾2\mathrm{and}b⩾-2$$$$\mathrm{now}b-a\mathrm{is}\mathrm{minimum}\mathrm{when}b\mathrm{is}\mathrm{minimum}$$$$b\mathrm{is}\mathrm{minimum}\mathrm{when}b=-2$$$$\Rightarrow a-2⩽9\Rightarrow a⩽11$$$$\mathrm{now}\min (b-a)=-2-11=-13.$$$$\mathrm{is}\mathrm{that}\mathrm{correct}\mathrm{sir}?$$

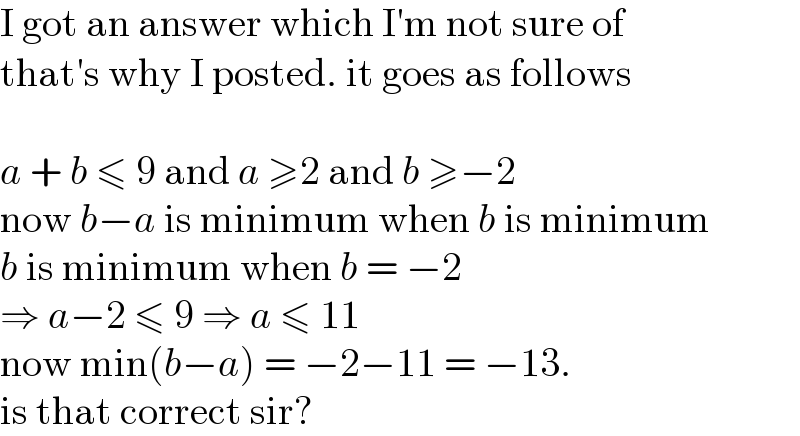
Commented by Rasheed.Sindhi last updated on 16/Aug/22

$$\mathbb{T}\mathrm{han}\mathbb{k}\mathrm{s}\mathrm{JDamian}\mathrm{sir}!$$

Answered by Frix last updated on 15/Aug/22

$$a+b⩽9\wedge a⩾2\wedge b⩾-2$$$$a=2+p^2\wedge b=-2+q^2$$$$a+b⩽9\Rightarrow p^2+q^2⩽9\Rightarrow q^2⩽9-p^2$$$$b-a⩾m\Rightarrow -p^2+q^2-4⩾m\Rightarrow q^2⩾m+p^2+4$$$$m+p^2+4⩽9-p^2$$$$m⩽5-2p^2$$$$m\mathrm{is}\min \mathrm{when}{p}^2\mathrm{is}\max$$$$p^2+q^2⩽9\Rightarrow \max \left(p^2\right)=9$$$$\Rightarrow q^2=0$$$$m=-13$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com