
Question and Answers Forum
Question Number 175051 by Mathspace last updated on 17/Aug/22
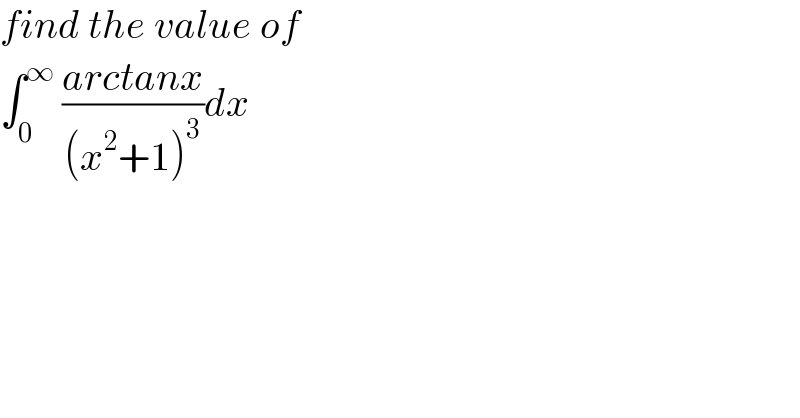
Commented by mokys last updated on 20/Aug/22
![I = ∫_0 ^( ∞) ((arctan x)/(( x^2 + 1 )^3 )) dx x = tany → dx = sec^2 y dx x= 0 → y = 0 , x→∞ ⇒ y = (𝛑/2) I = ∫_0 ^( (𝛑/2)) y cos^4 y dy u = y → du = dy , dv = cos^4 y → v = ((sin4y + 8 sin2y +12y)/(32)) I = [ ((y sin4y + 8 y sin2y + 12 y^2 )/(32))]_0 ^( (𝛑/2)) − (1/(32)) ∫_0 ^( (𝛑/2)) (sin4y +8 sin2y + 12y ) dy I = [ ((3 𝛑^2 )/(32)) ] − (1/(32)) [ − ((cos4y)/4) − 4 cos2y + 6 y^2 ]_( 0) ^( (𝛑/2)) I = ((3 𝛑^2 )/(32)) − (1/(32)) [ ( −(1/4) + 4 + ((3 𝛑^2 )/2) ) − ( − (1/4) −4 )] I = ((3 𝛑^2 )/(32)) − (1/(32)) [ ((16 + 3 𝛑^2 )/2) ] = ((6 𝛑^2 − 16 − 3 𝛑^2 )/(64)) = ((3 𝛑^2 − 16)/(64)) Aldolaimy Mohammad](Q175131.png)
Commented by Tawa11 last updated on 20/Aug/22

| ||
Question and Answers Forum | ||
Question Number 175051 by Mathspace last updated on 17/Aug/22 | ||
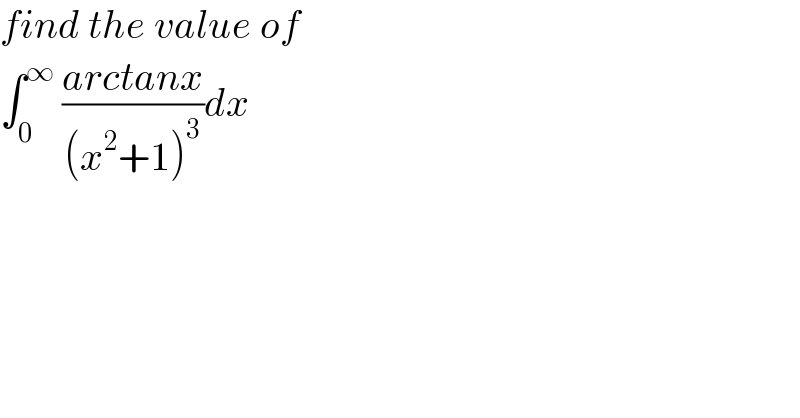 | ||
Commented by mokys last updated on 20/Aug/22 | ||
![I = ∫_0 ^( ∞) ((arctan x)/(( x^2 + 1 )^3 )) dx x = tany → dx = sec^2 y dx x= 0 → y = 0 , x→∞ ⇒ y = (𝛑/2) I = ∫_0 ^( (𝛑/2)) y cos^4 y dy u = y → du = dy , dv = cos^4 y → v = ((sin4y + 8 sin2y +12y)/(32)) I = [ ((y sin4y + 8 y sin2y + 12 y^2 )/(32))]_0 ^( (𝛑/2)) − (1/(32)) ∫_0 ^( (𝛑/2)) (sin4y +8 sin2y + 12y ) dy I = [ ((3 𝛑^2 )/(32)) ] − (1/(32)) [ − ((cos4y)/4) − 4 cos2y + 6 y^2 ]_( 0) ^( (𝛑/2)) I = ((3 𝛑^2 )/(32)) − (1/(32)) [ ( −(1/4) + 4 + ((3 𝛑^2 )/2) ) − ( − (1/4) −4 )] I = ((3 𝛑^2 )/(32)) − (1/(32)) [ ((16 + 3 𝛑^2 )/2) ] = ((6 𝛑^2 − 16 − 3 𝛑^2 )/(64)) = ((3 𝛑^2 − 16)/(64)) Aldolaimy Mohammad](Q175131.png) | ||
Commented by Tawa11 last updated on 20/Aug/22 | ||
 | ||