Prove that determinant ((1,1,1),(a,b,c),(a^2 ,b^2 ,c^2 ))= (a−b)(b−c)(c−a)


Question and Answers Forum

All Questions Topic List
Matrices and Determinants Questions
Previous in All Question Next in All Question
Previous in Matrices and Determinants Next in Matrices and Determinants
Question Number 175110 by nadovic last updated on 19/Aug/22

$Prove that \| \begin{matrix} 1 & 1 & 1 \\ a & b & c \\ a^{2} & b^{2} & c^{2} \end{matrix} \| = (a - b) (b - c) (c - a)$
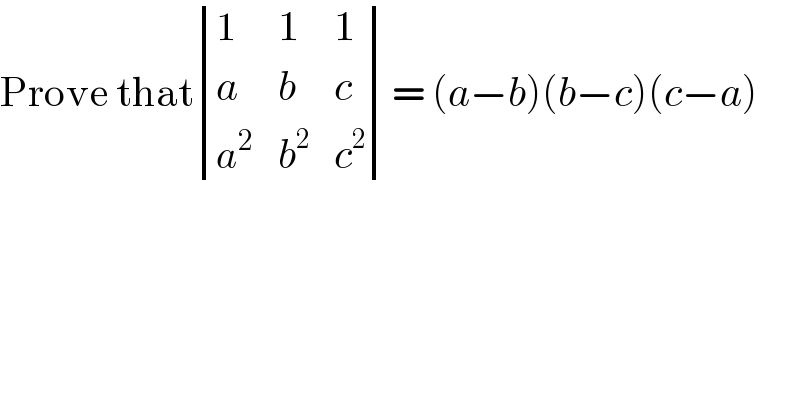
Commented by kaivan.ahmadi last updated on 19/Aug/22

$\| \begin{matrix} 1 1 1 \\ a b c \\ a^{2} b^{2} c^{2} \end{matrix} \| \| \begin{matrix} 1 1 1 \\ a b c \\ a^{2} b^{2} c^{2} \end{matrix} \| =$ $({b c}^{2} + {c a}^{2} + {a b}^{2}) - ({b a}^{2} + {a c}^{2} + {c b}^{2})$ $= c (b c + a^{2} - a c - b^{2}) - a b (a - b)$ $= c (c (b - a) + (a - b) (a + b)) - a b (a - b)$ $= (a - b) (- c^{2} + a c + b c - a b)$ $= (a - b) (c (a - c) + b (c - a))$ $= (a - b) ((c - a) (b - c)) =$ $(a - b) (b - c) (c - a)$ $n o t e t h a t t h i s i s a V a n d e r m o n d e$ $d e t e r m i n a n t .$ $I n g e n e r a l c a s e$ $\| \begin{matrix} 1 1 . . . 1 \\ a_{1} a_{2} . . . a_{n} \\ ⋮ ⋮ ⋮ \\ a_{1}^{n - 1} . . . a_{n}^{n - 1} \end{matrix} \| = \prod_{1 ⩽ i < j ⩽ n} (a_{j} - a_{i})$
Commented by Tawa11 last updated on 19/Aug/22

$Great sir .$
Commented by puissant last updated on 21/Aug/22

$V a n d e r m o n d e m e t h o d$
	Answered by Rasheed.Sindhi last updated on 19/Aug/22
	$Prove that determinant ((1,1,1),(a,b,c),(a^2 ,b^2 ,c^2 ))= (a−b)(b−c)(c−a) ∣ (/)Through properties(/) ∣ ^(−) = determinant ((1,( 0),( 0)),(a,(b−a),(c−a)),(a^2 ,(b^2 −a^2 ),(c^2 −a^2 )))C2−C1_(C3−C1) =(b−a)(c−a) determinant ((1,( 0),( 0)),(a,( 1),( 1)),(a^2 ,(b+a),(c+a))) =(b−a)(c−a)∙1{1(c+a)−1(b+a)} =(b−a)(c−a)(c−b) =(a−b)(b−c)(c−a)$
	$Prove that \| \begin{matrix} 1 & 1 & 1 \\ a & b & c \\ a^{2} & b^{2} & c^{2} \end{matrix} \| = (a - b) (b - c) (c - a)$ $\overset{―}{\underset{―}{∣} \underset{―}{\frac{}{} Through properties \frac{}{} ∣}}$ $= \| \begin{matrix} 1 & 0 & 0 \\ a & b - a & c - a \\ a^{2} & b^{2} - a^{2} & c^{2} - a^{2} \end{matrix} \| \underset{C 3 - C 1}{C 2 - C 1}$ $= (b - a) (c - a) \| \begin{matrix} 1 & 0 & 0 \\ a & 1 & 1 \\ a^{2} & b + a & c + a \end{matrix} \|$ $= (b - a) (c - a) \cdot 1 {1 (c + a) - 1 (b + a)}$ $= (b - a) (c - a) (c - b)$ $= (a - b) (b - c) (c - a)$
	Commented by puissant last updated on 21/Aug/22

	$G r e a t$
	Commented by Rasheed.Sindhi last updated on 21/Aug/22

	$T h a n k s s i r!$
	Answered by Rajpurohith last updated on 10/Jun/23

	$A p p l y t h e o p e r a t i o n C_{1} \to C_{1} - C_{2} a n d C_{2} \to C_{2} - C_{3}$ $T h e d e t e r m i n a n t r e d u c e s t o,$ $\| \begin{matrix} 0 0 1 \\ a - b b - c c \\ a^{2} - b^{2} b^{2} - c^{2} c^{2} \end{matrix} \| = (a - b) (b - c) \| \begin{matrix} 0 0 1 \\ 1 1 c \\ a + b b + c c^{2} \end{matrix} \|$ $T h i s i s b y t a k i n g t h e c o m m o n f a c t o r s f r o m C_{1} & C_{2}$ $a n d o p e r a t e C_{1} \to C_{1} - C_{2}$ $= (a - b) (b - c) \| \begin{matrix} 0 0 1 \\ 0 1 c \\ a - c b + c c^{2} \end{matrix} \|$ $e x p a n d i n g a l o n g t h e f i r s t r o w,$ $= (a - b) (b - c) (c - a)$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum