Question Number 175115 by mnjuly1970 last updated on 19/Aug/22
Answered by aleks041103 last updated on 19/Aug/22
$${n}\rightarrow\infty \\ $$$$\sqrt{\mathrm{1}+\frac{{k}}{{n}^{\mathrm{2}} }}−\mathrm{1}=\left(\mathrm{1}+\frac{{k}}{\mathrm{2}{n}^{\mathrm{2}} }\right)−\mathrm{1}=\frac{{k}}{\mathrm{2}{n}^{\mathrm{2}} } \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {{lim}}\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\sqrt{\mathrm{1}+\frac{{k}}{{n}^{\mathrm{2}} }}−\mathrm{1}\right)=\underset{{n}\rightarrow\infty} {{lim}}\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}= \\ $$$$=\underset{{n}\rightarrow\infty} {{lim}}\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }\:\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{4}}\underset{{n}\rightarrow\infty} {{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
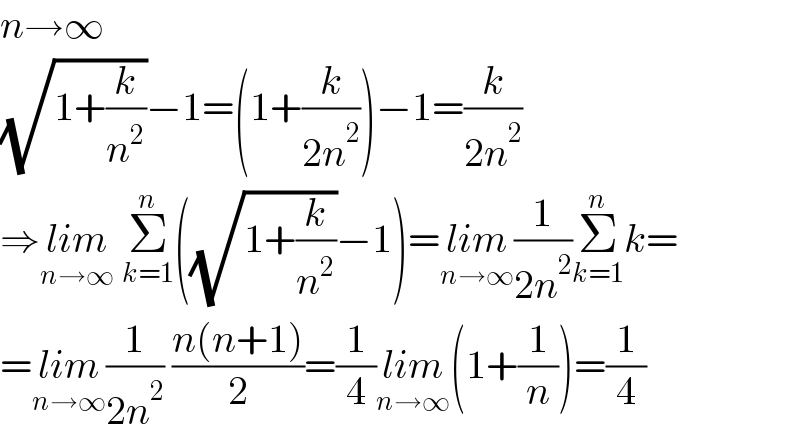
Commented by mnjuly1970 last updated on 20/Aug/22
$${thanks}\:{alot}\:{sir} \\ $$
Answered by CElcedricjunior last updated on 20/Aug/22
![lim_(x→∞) Σ_(k=1) ^n ((√(1+(k/n^2 ))) −1)=(1/4) or ((1+a))^(1/n) =(1+a)^n ≈1+na avec a<<<1 =>(√(1+(k/n^2 ))) =(1+(k/n^2 ))^(1/2) ≈1+(k/(2n^2 )) ≈lim_(x→∞) Σ_(k=1) ^n (k/(2n^2 ))=lim_(x→∞) (1/(2n))Σ_(k=1) ^n (k/n) lim_(x→∞) Σ_(k=1) ^n ((√(1+(k/n^2 ))) −1)≈(1/2)∫_0 ^1 xdx ≈(1/2)[(x^2 /2)]_0 ^1 ⇔lim_(x→∞) Σ_(k=1) ^n ((√(1+(k/n^2 )))−1)≈(1/4) ..........le celebre cedric junior.........](Q175126.png)
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\sum}}\left(\sqrt{\mathrm{1}+\frac{\boldsymbol{{k}}}{\boldsymbol{{n}}^{\mathrm{2}} }}\:−\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\boldsymbol{{or}}\:\sqrt[{\boldsymbol{{n}}}]{\mathrm{1}+\boldsymbol{{a}}}=\left(\mathrm{1}+\boldsymbol{{a}}\right)^{\boldsymbol{{n}}} \approx\mathrm{1}+\boldsymbol{{na}}\:\boldsymbol{{avec}}\:\boldsymbol{{a}}<<<\mathrm{1} \\ $$$$=>\sqrt{\mathrm{1}+\frac{\boldsymbol{{k}}}{\boldsymbol{{n}}^{\mathrm{2}} }}\:=\left(\mathrm{1}+\frac{\boldsymbol{{k}}}{\boldsymbol{{n}}^{\mathrm{2}} }\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \approx\mathrm{1}+\frac{\boldsymbol{{k}}}{\mathrm{2}\boldsymbol{{n}}^{\mathrm{2}} } \\ $$$$\approx\underset{{x}\rightarrow\infty} {\mathrm{lim}}\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\sum}}\frac{\boldsymbol{{k}}}{\mathrm{2}\boldsymbol{{n}}^{\mathrm{2}} }=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{n}}}\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\sum}}\frac{\boldsymbol{{k}}}{\boldsymbol{{n}}} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\sum}}\left(\sqrt{\mathrm{1}+\frac{\boldsymbol{{k}}}{\boldsymbol{{n}}^{\mathrm{2}} }}\:−\mathrm{1}\right)\approx\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{{xdx}} \\ $$$$\approx\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\Leftrightarrow\underset{{x}\rightarrow\infty} {\mathrm{lim}}\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\sum}}\left(\sqrt{\mathrm{1}+\frac{\boldsymbol{{k}}}{\boldsymbol{{n}}^{\mathrm{2}} }}−\mathrm{1}\right)\approx\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\: \\ $$$$..........{le}\:{celebre}\:{cedric}\:{junior}......... \\ $$
Commented by mnjuly1970 last updated on 20/Aug/22
$${mercey}\:{sir} \\ $$
Commented by Tawa11 last updated on 20/Aug/22
$$\mathrm{Great}\:\mathrm{sirs} \\ $$