
Question and Answers Forum
Question Number 175175 by Shrinava last updated on 21/Aug/22
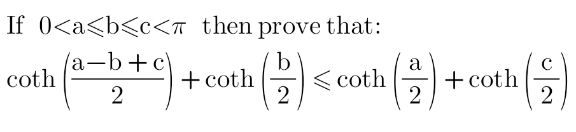
Answered by TheHoneyCat last updated on 23/Aug/22
![Let me proove a slightly more general statement: let x=(a/2) ≤ y=(c/2) let t∈[0,1] : t.x+(1−t).y=b and let us proove that e^x +e^(−x) +e^y +e^(−y) −e^(tx+(1−t)y) −e^(−tx−(1−t)y) −e^((1−t)x+ty) −e^(−(1−t)x+ty) ≥0 Notice that the problem written this way is in fact equivalent to your question (exept I got read of the π upper limit, it was unnecesarry) Also note that the problem beeing perfectly symetric in t by the transformation t (1−t) so in fact we only need to verrify for t∈[0,(1/2)] let′s go if t=0 the problem is equivalent to: e^x +e^(−x) +e^y +e^(−y) −e^y −e^(−y) −e^x −e^(−x) =0≥0 so t=0 works Now let′s show that the function of t, wich we want to say positive, is increasing from now on: its derivative will be: −(x−y)e^(tx+(1−t)y) −(y−x)e^(−tx−(1−t)y) −(y−x)e^((1−t)x+ty) −(x−y)e^(−(1−t)x−ty) Considering only the first line D_1 (t):= (y−x)(e^b −e^(−b) ) b≥0 so (e^b −e^(−b) )≥0 and y−x≥0 so D_1 ≥0 you can show the same thing for the second line but everything is inverted (you′ll need to use t≤1/2 but that′s not a problem as we said earlier) So the function is increasing on [0,1/2] So it stays positive on the whole interval We conclude the proof, as we said, by symetry arround 1/2. □ hope that answeres your question.](Q175204.png)
| ||
Question and Answers Forum | ||
Question Number 175175 by Shrinava last updated on 21/Aug/22 | ||
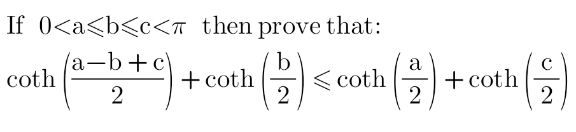 | ||
Answered by TheHoneyCat last updated on 23/Aug/22 | ||
![Let me proove a slightly more general statement: let x=(a/2) ≤ y=(c/2) let t∈[0,1] : t.x+(1−t).y=b and let us proove that e^x +e^(−x) +e^y +e^(−y) −e^(tx+(1−t)y) −e^(−tx−(1−t)y) −e^((1−t)x+ty) −e^(−(1−t)x+ty) ≥0 Notice that the problem written this way is in fact equivalent to your question (exept I got read of the π upper limit, it was unnecesarry) Also note that the problem beeing perfectly symetric in t by the transformation t (1−t) so in fact we only need to verrify for t∈[0,(1/2)] let′s go if t=0 the problem is equivalent to: e^x +e^(−x) +e^y +e^(−y) −e^y −e^(−y) −e^x −e^(−x) =0≥0 so t=0 works Now let′s show that the function of t, wich we want to say positive, is increasing from now on: its derivative will be: −(x−y)e^(tx+(1−t)y) −(y−x)e^(−tx−(1−t)y) −(y−x)e^((1−t)x+ty) −(x−y)e^(−(1−t)x−ty) Considering only the first line D_1 (t):= (y−x)(e^b −e^(−b) ) b≥0 so (e^b −e^(−b) )≥0 and y−x≥0 so D_1 ≥0 you can show the same thing for the second line but everything is inverted (you′ll need to use t≤1/2 but that′s not a problem as we said earlier) So the function is increasing on [0,1/2] So it stays positive on the whole interval We conclude the proof, as we said, by symetry arround 1/2. □ hope that answeres your question.](Q175204.png) | ||
| ||