Question Number 175247 by rexford last updated on 24/Aug/22
Answered by Ar Brandon last updated on 24/Aug/22
![I=∫_0 ^(π/2) sin^2 4ϑcos^5 4ϑdϑ =∫_0 ^(π/2) sin^2 4ϑ(1−sin^2 4ϑ)^2 cos4ϑdϑ =∫_0 ^(π/2) (sin^2 4ϑ−2sin^4 4ϑ+sin^6 4ϑ)cos4ϑdϑ =(1/4)[((sin^3 4ϑ)/3)−((2sin^5 4ϑ)/5)+((sin^7 4ϑ)/7)]_0 ^(π/2) =0](Q175249.png)
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2}} \mathrm{4}\vartheta\mathrm{cos}^{\mathrm{5}} \mathrm{4}\vartheta{d}\vartheta \\ $$$$\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2}} \mathrm{4}\vartheta\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{4}\vartheta\right)^{\mathrm{2}} \mathrm{cos4}\vartheta{d}\vartheta \\ $$$$\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{sin}^{\mathrm{2}} \mathrm{4}\vartheta−\mathrm{2sin}^{\mathrm{4}} \mathrm{4}\vartheta+\mathrm{sin}^{\mathrm{6}} \mathrm{4}\vartheta\right)\mathrm{cos4}\vartheta{d}\vartheta \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{4}}\left[\frac{\mathrm{sin}^{\mathrm{3}} \mathrm{4}\vartheta}{\mathrm{3}}−\frac{\mathrm{2sin}^{\mathrm{5}} \mathrm{4}\vartheta}{\mathrm{5}}+\frac{\mathrm{sin}^{\mathrm{7}} \mathrm{4}\vartheta}{\mathrm{7}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\mathrm{0} \\ $$
Commented by rexford last updated on 25/Aug/22
$${But}\:{the}\:{answer}\:{is}\:{not}\:{zero}\:{when}\:{typed}\:{on}\:{calculator} \\ $$
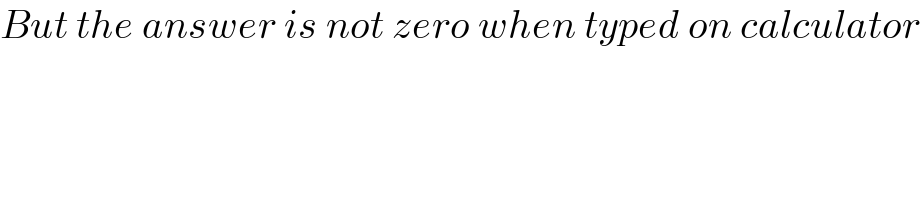
Commented by Ar Brandon last updated on 25/Aug/22
$$\mathrm{Then}\:\mathrm{maybe}\:\mathrm{you}\:\mathrm{should}\:\mathrm{sell}\:\mathrm{the}\:\mathrm{calculator} \\ $$$$\:\mathrm{and}\:\mathrm{have}\:\mathrm{a}\:\mathrm{picnic}\:\mathrm{with}\:\mathrm{the}\:\mathrm{money}.\:\mathrm{Haha}\:! \\ $$
Commented by rexford last updated on 25/Aug/22
$${i}\:{see}...{lol} \\ $$
Commented by Ar Brandon last updated on 25/Aug/22
![What your calculator gives you is probably the sum of areas bounded by f(x) and the x-axis which is [((sin^3 4ϑ)/3)−((2sin^5 4ϑ)/5)+((sin^7 4ϑ)/7)]_0 ^(π/8) =(1/3)−(1/5)+(1/7)=((29)/(105)) square units](Q175259.png)
$$\mathrm{What}\:\mathrm{your}\:\mathrm{calculator}\:\mathrm{gives}\:\mathrm{you}\:\mathrm{is}\:\mathrm{probably} \\ $$$$\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{areas}\:\mathrm{bounded}\:\mathrm{by}\:\mathrm{f}\left({x}\right)\:\mathrm{and}\:\mathrm{the} \\ $$$${x}-\mathrm{axis}\:\mathrm{which}\:\mathrm{is} \\ $$$$\left[\frac{\mathrm{sin}^{\mathrm{3}} \mathrm{4}\vartheta}{\mathrm{3}}−\frac{\mathrm{2sin}^{\mathrm{5}} \mathrm{4}\vartheta}{\mathrm{5}}+\frac{\mathrm{sin}^{\mathrm{7}} \mathrm{4}\vartheta}{\mathrm{7}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{8}}} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{7}}=\frac{\mathrm{29}}{\mathrm{105}}\:\mathrm{square}\:\mathrm{units} \\ $$
Commented by Ar Brandon last updated on 25/Aug/22
Commented by rexford last updated on 25/Aug/22
$${I}\:{get}\:{it},{Boss} \\ $$$$...{but}\:{is}\:{there}\:{any}\:{approach} \\ $$$$\:{to}\:{relate}\:{the}\:{integral}\:{with}\:{the}\: \\ $$$${beta}\:{integral}\:{i}.{e}\:\mathrm{2}\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} {sin}^{\mathrm{2}{m}−\mathrm{1}} \theta{cos}^{\mathrm{2}{n}+\mathrm{1}} \theta{d}\theta \\ $$
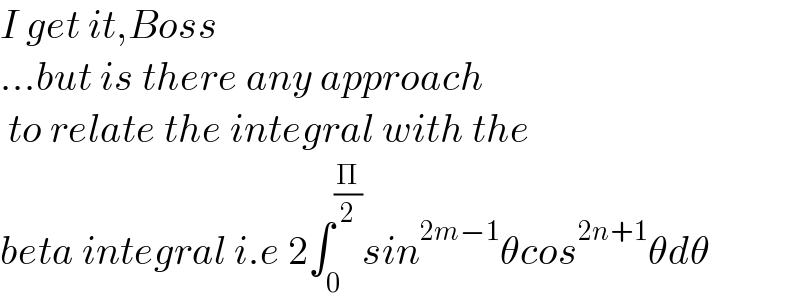
Commented by Ar Brandon last updated on 25/Aug/22
![Yah sure ! I=∫_0 ^(π/2) sin^2 4ϑcos^5 4ϑdϑ=(1/4)∫_0 ^(2π) sin^2 tcos^5 tdt 4I=∫_0 ^(π/2) sin^2 tcos^5 tdt_(A) +∫_(π/2) ^π sin^2 tcos^5 tdt_(B) +∫_π ^((3π)/2) sin^2 tcos^5 tdt_(C) +∫_((3π)/2) ^(2π) sin^2 tcos^5 tdt_(D) For B let t=π−u ⇒B=∫_0 ^(π/2) sin^2 (π−u)cos^5 (π−u)du ⇒B=−∫_0 ^(π/2) sin^2 ucos^5 udu=−A since sin(π−u)=sinu, cos(π−u)=−cosu Similarly for C we let t=((3π)/2)−u and we have −∫_0 ^(π/2) cos^2 usin^5 udu, since sin(((3π)/2)−u)=−cosu and cos(((3π)/2)−u)=−sinu which is equal to −∫_0 ^(π/2) sin^2 ucos^5 udu since ∫_0 ^(π/2) sin^m ucos^n udu=∫_0 ^(π/2) cos^m usin^n udu And for D when we let t=2π−t we have ∫_0 ^(π/2) sin^2 ucos^5 udu So I=∫_0 ^(π/2) sin^2 tcos^5 tdt−∫_0 ^(π/2) sin^2 ucos^5 udu−∫_0 ^(π/2) sin^2 ucos^5 udu+∫_0 ^(π/2) sin^2 ucos^5 udu Now you can apply your beta function since we now have the usual limits [0, (π/2)]. Although that will be superfluous since we can already notice all the partial integrals cancel out themselves A−A−A+A=0](Q175274.png)
$$\mathrm{Yah}\:\mathrm{sure}\:! \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2}} \mathrm{4}\vartheta\mathrm{cos}^{\mathrm{5}} \mathrm{4}\vartheta{d}\vartheta=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mathrm{sin}^{\mathrm{2}} {t}\mathrm{cos}^{\mathrm{5}} {tdt} \\ $$$$\mathrm{4}{I}=\underset{{A}} {\underbrace{\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2}} {t}\mathrm{cos}^{\mathrm{5}} {tdt}}}+\underset{{B}} {\underbrace{\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \mathrm{sin}^{\mathrm{2}} {t}\mathrm{cos}^{\mathrm{5}} {tdt}}}+\underset{{C}} {\underbrace{\int_{\pi} ^{\frac{\mathrm{3}\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2}} {t}\mathrm{cos}^{\mathrm{5}} {tdt}}}+\underset{{D}} {\underbrace{\int_{\frac{\mathrm{3}\pi}{\mathrm{2}}} ^{\mathrm{2}\pi} \mathrm{sin}^{\mathrm{2}} {t}\mathrm{cos}^{\mathrm{5}} {tdt}}} \\ $$$$\mathrm{For}\:{B}\:\mathrm{let}\:{t}=\pi−{u}\:\Rightarrow{B}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2}} \left(\pi−{u}\right)\mathrm{cos}^{\mathrm{5}} \left(\pi−{u}\right){du} \\ $$$$\Rightarrow{B}=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2}} {u}\mathrm{cos}^{\mathrm{5}} {udu}=−{A}\:\mathrm{since}\:\mathrm{sin}\left(\pi−{u}\right)=\mathrm{sin}{u},\:\mathrm{cos}\left(\pi−{u}\right)=−\mathrm{cos}{u} \\ $$$$\mathrm{Similarly}\:\mathrm{for}\:{C}\:\mathrm{we}\:\mathrm{let}\:{t}=\frac{\mathrm{3}\pi}{\mathrm{2}}−{u}\:\mathrm{and}\:\mathrm{we}\:\mathrm{have} \\ $$$$−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{2}} {u}\mathrm{sin}^{\mathrm{5}} {udu},\:\mathrm{since}\:\mathrm{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{2}}−{u}\right)=−\mathrm{cos}{u}\:\mathrm{and}\:\mathrm{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{2}}−{u}\right)=−\mathrm{sin}{u} \\ $$$$\mathrm{which}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2}} {u}\mathrm{cos}^{\mathrm{5}} {udu}\:\mathrm{since}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{{m}} {u}\mathrm{cos}^{{n}} {udu}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{{m}} {u}\mathrm{sin}^{{n}} {udu} \\ $$$$\mathrm{And}\:\mathrm{for}\:{D}\:\mathrm{when}\:\mathrm{we}\:\mathrm{let}\:{t}=\mathrm{2}\pi−{t}\:\mathrm{we}\:\mathrm{have}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2}} {u}\mathrm{cos}^{\mathrm{5}} {udu} \\ $$$$\mathrm{So}\: \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2}} {t}\mathrm{cos}^{\mathrm{5}} {tdt}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2}} {u}\mathrm{cos}^{\mathrm{5}} {udu}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2}} {u}\mathrm{cos}^{\mathrm{5}} {udu}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2}} {u}\mathrm{cos}^{\mathrm{5}} {udu} \\ $$$$\mathrm{Now}\:\mathrm{you}\:\mathrm{can}\:\mathrm{apply}\:\mathrm{your}\:\mathrm{beta}\:\mathrm{function}\:\mathrm{since}\:\mathrm{we}\:\mathrm{now}\:\mathrm{have}\:\mathrm{the}\:\mathrm{usual}\:\mathrm{limits} \\ $$$$\left[\mathrm{0},\:\frac{\pi}{\mathrm{2}}\right].\:\mathrm{Although}\:\mathrm{that}\:\mathrm{will}\:\mathrm{be}\:\mathrm{superfluous}\:\mathrm{since}\:\mathrm{we}\:\mathrm{can}\:\mathrm{already}\:\mathrm{notice} \\ $$$$\:\mathrm{all}\:\mathrm{the}\:\mathrm{partial}\:\mathrm{integrals}\:\mathrm{cancel}\:\mathrm{out}\:\mathrm{themselves} \\ $$$${A}−{A}−{A}+{A}=\mathrm{0} \\ $$
Answered by Mathspace last updated on 25/Aug/22
$$\Psi=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}} \left(\mathrm{4}\theta\right){cos}^{\mathrm{5}} \left(\mathrm{4}\theta\right){d}\theta \\ $$$$=_{\mathrm{4}\theta={t}} \:\:\:\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{2}\pi} {sin}^{\mathrm{2}} {t}\:{cos}^{\mathrm{5}} {t}\:{dt} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} {sin}^{\mathrm{2}} {t}\:{cos}^{\mathrm{5}} {t}\:{dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(...\right){dt}\:+\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \left(...\right){dt}+\int_{\pi} ^{\frac{\mathrm{3}\pi}{\mathrm{2}}} \left(...\right){dt} \\ $$$$+\int_{\frac{\mathrm{3}\pi}{\mathrm{2}}} ^{\mathrm{2}\pi} \left(...\right){dt} \\ $$$$\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} {sin}^{\mathrm{2}} {t}\:{cos}^{\mathrm{5}} {t}\:{dt} \\ $$$$=_{{t}=\frac{\pi}{\mathrm{2}}+{x}} \:\:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}} {x}\:{sin}^{\mathrm{5}} {xdx} \\ $$$$\int_{\pi} ^{\frac{\mathrm{3}\pi}{\mathrm{2}}} {sin}^{\mathrm{2}} {t}\:{cos}^{\mathrm{5}} {t}\:{dt} \\ $$$$=_{{t}=\pi+{x}} \:−\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}} {x}\:{cos}^{\mathrm{5}} {xdx} \\ $$$$\int_{\frac{\mathrm{3}\pi}{\mathrm{2}}} ^{\mathrm{2}\pi} {sin}^{\mathrm{2}} {t}\:{cos}^{\mathrm{5}} {t}\:{dt} \\ $$$$=_{{t}=\frac{\mathrm{3}\pi}{\mathrm{2}}+{x}} \:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{2}} {x}\:{sin}^{\mathrm{5}} {xdx}\:\Rightarrow \\ $$$$\mathrm{4}\Psi=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}} {x}\:{cos}^{\mathrm{5}} {xdx}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}} {x}\:{sin}^{\mathrm{5}} {xdx} \\ $$$$−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}} {x}\:{cos}^{\mathrm{5}} {xdx}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}} {x}\:{sin}^{\mathrm{5}} {xdx} \\ $$$$=\mathrm{0}\:\Rightarrow\Psi=\mathrm{0} \\ $$