7+67+667+6667+.....(n terms)=?


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 175411 by Rasheed.Sindhi last updated on 29/Aug/22

$7 + 67 + 667 + 6667 + . . . . . (n t e r m s) = ?$
Commented by infinityaction last updated on 30/Aug/22

$(6 + 1) + (66 + 1) + (666 + 1) + . . . (n t e r m s)$ $6 + 66 + . . . + n t e r m s + 1 + 1 + 1 . . . n t e r m s$ $6 [1 + 11 + 111 + . . + 1 (n t e r m s)] + n (1)$ $S_{n} = 1 + 11 + 111 + . . . + 1111 . . . 11$ $9 S_{n} = 9 + 99 + 999 + . . . + 999 . . . 99$ $= (10 - 1) + (100 - 1) + (1000 - 1) + . . . n t e r m s$ $= (10 + 100 + 1000 + . . . n t e r m s) - n$ $= \frac{10 (10^{n} - 1)}{10 - 1} - n$ $= \frac{10 (10^{n} - 1) - 9 n}{9}$ $S_{n} = \frac{10^{n + 1} - 9 n - 10}{81}$ $t h e n b y {e q}^{n} (1)$ $6 [\frac{10^{n + 1} - 9 n - 10}{81}] + n$ $\frac{2}{27} [10^{n + 1} - 9 n - 10] + n$ $\frac{2 \times 10^{n + 1} - 18 n + 27 n - 20}{27}$ $\frac{2 \times 10^{n + 1} + 9 n - 20}{27}$
Commented by Rasheed.Sindhi last updated on 30/Aug/22

$T han k s to all sirs for their good &$ $unique approaches!$
Commented by peter frank last updated on 31/Aug/22

$thanks$
	Answered by Ar Brandon last updated on 29/Aug/22
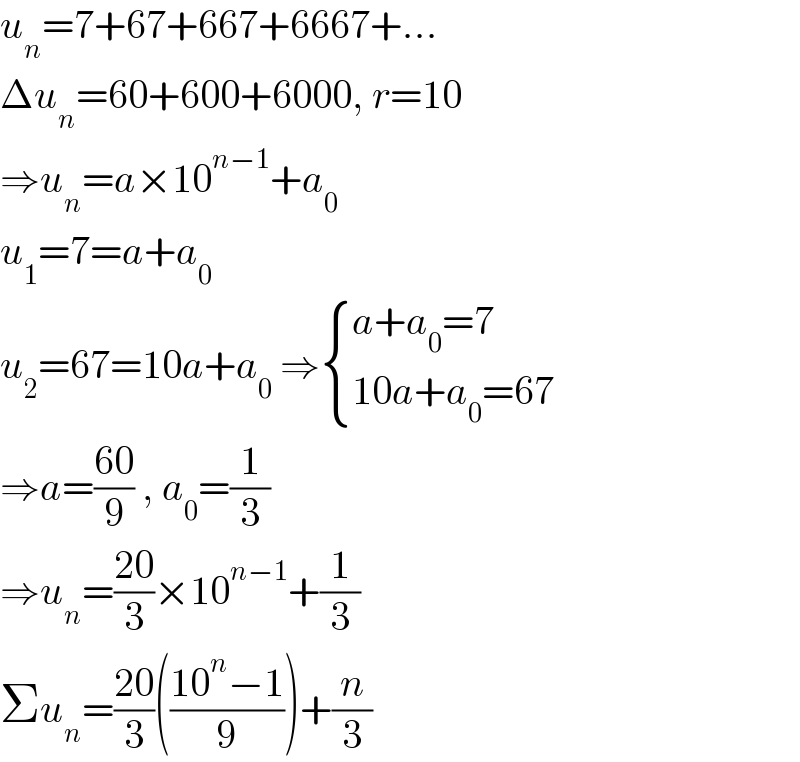
	$u_n =7+67+667+6667+... Δu_n =60+600+6000, r=10 ⇒u_n =a×10^(n−1) +a_0 u_1 =7=a+a_0 u_2 =67=10a+a_0 ⇒ { ((a+a_0 =7)),((10a+a_0 =67)) :} ⇒a=((60)/9) , a_0 =(1/3) ⇒u_n =((20)/3)×10^(n−1) +(1/3) Σu_n =((20)/3)(((10^n −1)/9))+(n/3)$
	$u_{n} = 7 + 67 + 667 + 6667 + . . .$ $Δ u_{n} = 60 + 600 + 6000, r = 10$ $\Rightarrow u_{n} = a \times 10^{n - 1} + a_{0}$ $u_{1} = 7 = a + a_{0}$ $u_{2} = 67 = 10 a + a_{0} \Rightarrow {\begin{cases} a + a_{0} = 7 \\ 10 a + a_{0} = 67 \end{cases}$ $\Rightarrow a = \frac{60}{9}, a_{0} = \frac{1}{3}$ $\Rightarrow u_{n} = \frac{20}{3} \times 10^{n - 1} + \frac{1}{3}$ $Σ u_{n} = \frac{20}{3} (\frac{10^{n} - 1}{9}) + \frac{n}{3}$
	Answered by Rasheed.Sindhi last updated on 30/Aug/22
	$S=7+67+667+6667+.....(n terms) S=(10−3)+(100−33)+(1000−333)+...(n terms) ={10+100+100+...(n terms)}_(S1) −{3+33+333+...(n terms)} =S_1 −(3/9)(9+99+999+...(n terms) =S_1 −(1/3)(10−1+100−1+1000−1+...(n terms) =S_1 −(1/3){10+100+1000+...(n terms)−n} =S_1 −(1/3){S_1 −n} =(2/3)S_1 +(1/3)n ∵ S_1 =((10(10^n −1))/(10−1))=((10^(n+1) −10)/9) ∴S_n =(2/3)(((10^(n+1) −10)/9))+(1/3)n =((2∙10^(n+1) −20)/(27))+(n/3) =((2∙10^(n+1) +9n−20)/(27))$
	$S = 7 + 67 + 667 + 6667 + . . . . . (n t e r m s)$ $S = (10 - 3) + (100 - 33) + (1000 - 333) + . . . (n t e r m s)$ $= \underset{S 1}{\underset{⏟}{{10 + 100 + 100 + . . . (n t e r m s)}}}$ $- {3 + 33 + 333 + . . . (n t e r m s)}$ $= S_{1} - \frac{3}{9} (9 + 99 + 999 + . . . (n t e r m s)$ $= S_{1} - \frac{1}{3} (10 - 1 + 100 - 1 + 1000 - 1 + . . . (n t e r m s)$ $= S_{1} - \frac{1}{3} {10 + 100 + 1000 + . . . (n t e r m s) - n}$ $= S_{1} - \frac{1}{3} {S_{1} - n}$ $= \frac{2}{3} S_{1} + \frac{1}{3} n$ $∵ S_{1} = \frac{10 (10^{n} - 1)}{10 - 1} = \frac{10^{n + 1} - 10}{9}$ $∴ S_{n} = \frac{2}{3} (\frac{10^{n + 1} - 10}{9}) + \frac{1}{3} n$ $= \frac{2 \cdot 10^{n + 1} - 20}{27} + \frac{n}{3}$ $= \frac{2 \cdot 10^{n + 1} + 9 n - 20}{27}$
	Commented by Tawa11 last updated on 30/Aug/22

	$Great sirs$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum