Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 175674 by infinityaction last updated on 05/Sep/22

Answered by mr W last updated on 05/Sep/22

−(b/(2a))=2 ⇒b=−4a f(2)=4a+2b+c=c−4a f(1)=a+b+c=c−3a=f(3) f(f(1))=f(f(2)) a(c−3a)^2 −4a(c−3a)+c=a(c−4a)^2 −4a(c−4a)+c 2c−7a=4 ⇒c=2+((7a)/2) that means for any a≠0, f(x)=ax^2 −4ax+2+((7a)/2) fulfills f(f(1))=f(f(2))=f(f(3)).

$$−\frac{{b}}{\mathrm{2}{a}}=\mathrm{2}\:\Rightarrow{b}=−\mathrm{4}{a} \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{4}{a}+\mathrm{2}{b}+{c}={c}−\mathrm{4}{a} \\ $$$${f}\left(\mathrm{1}\right)={a}+{b}+{c}={c}−\mathrm{3}{a}={f}\left(\mathrm{3}\right) \\ $$$${f}\left({f}\left(\mathrm{1}\right)\right)={f}\left({f}\left(\mathrm{2}\right)\right) \\ $$$${a}\left({c}−\mathrm{3}{a}\right)^{\mathrm{2}} −\mathrm{4}{a}\left({c}−\mathrm{3}{a}\right)+{c}={a}\left({c}−\mathrm{4}{a}\right)^{\mathrm{2}} −\mathrm{4}{a}\left({c}−\mathrm{4}{a}\right)+{c} \\ $$$$\mathrm{2}{c}−\mathrm{7}{a}=\mathrm{4} \\ $$$$\Rightarrow{c}=\mathrm{2}+\frac{\mathrm{7}{a}}{\mathrm{2}} \\ $$$${that}\:{means}\:{for}\:{any}\:{a}\neq\mathrm{0},\: \\ $$$${f}\left({x}\right)={ax}^{\mathrm{2}} −\mathrm{4}{ax}+\mathrm{2}+\frac{\mathrm{7}{a}}{\mathrm{2}}\:{fulfills} \\ $$$${f}\left({f}\left(\mathrm{1}\right)\right)={f}\left({f}\left(\mathrm{2}\right)\right)={f}\left({f}\left(\mathrm{3}\right)\right). \\ $$

Commented by Rasheed.Sindhi last updated on 05/Sep/22

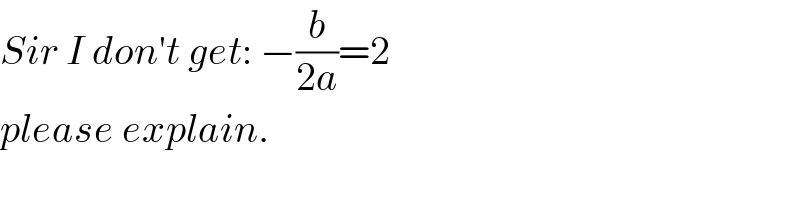
Sir I don′t get: −(b/(2a))=2 please explain.

$${Sir}\:{I}\:{don}'{t}\:{get}:\:−\frac{{b}}{\mathrm{2}{a}}=\mathrm{2}\: \\ $$$${please}\:{explain}. \\ $$

Commented by mr W last updated on 05/Sep/22

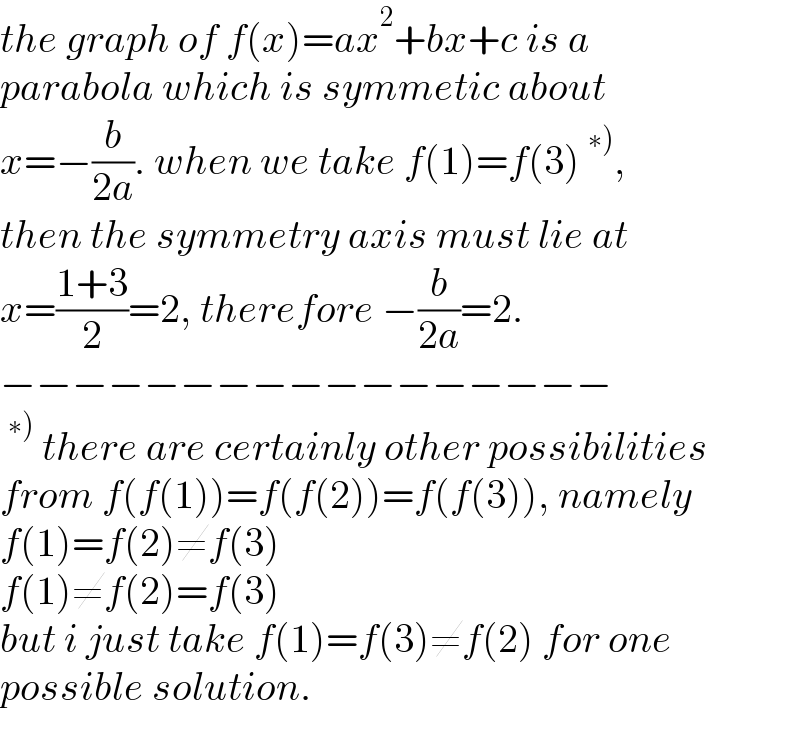
the graph of f(x)=ax^2 +bx+c is a parabola which is symmetic about x=−(b/(2a)). when we take f(1)=f(3)^(∗)) , then the symmetry axis must lie at x=((1+3)/2)=2, therefore −(b/(2a))=2. −−−−−−−−−−−−−−−−− ^(∗)) there are certainly other possibilities from f(f(1))=f(f(2))=f(f(3)), namely f(1)=f(2)≠f(3) f(1)≠f(2)=f(3) but i just take f(1)=f(3)≠f(2) for one possible solution.

$${the}\:{graph}\:{of}\:{f}\left({x}\right)={ax}^{\mathrm{2}} +{bx}+{c}\:{is}\:{a} \\ $$$${parabola}\:{which}\:{is}\:{symmetic}\:{about} \\ $$$${x}=−\frac{{b}}{\mathrm{2}{a}}.\:{when}\:{we}\:{take}\:{f}\left(\mathrm{1}\right)={f}\left(\mathrm{3}\right)\:^{\left.\ast\right)} , \\ $$$${then}\:{the}\:{symmetry}\:{axis}\:{must}\:{lie}\:{at}\: \\ $$$${x}=\frac{\mathrm{1}+\mathrm{3}}{\mathrm{2}}=\mathrm{2},\:{therefore}\:−\frac{{b}}{\mathrm{2}{a}}=\mathrm{2}. \\ $$$$−−−−−−−−−−−−−−−−− \\ $$$$\:^{\left.\ast\right)} \:{there}\:{are}\:{certainly}\:{other}\:{possibilities} \\ $$$${from}\:{f}\left({f}\left(\mathrm{1}\right)\right)={f}\left({f}\left(\mathrm{2}\right)\right)={f}\left({f}\left(\mathrm{3}\right)\right),\:{namely} \\ $$$${f}\left(\mathrm{1}\right)={f}\left(\mathrm{2}\right)\neq{f}\left(\mathrm{3}\right) \\ $$$${f}\left(\mathrm{1}\right)\neq{f}\left(\mathrm{2}\right)={f}\left(\mathrm{3}\right) \\ $$$${but}\:{i}\:{just}\:{take}\:{f}\left(\mathrm{1}\right)={f}\left(\mathrm{3}\right)\neq{f}\left(\mathrm{2}\right)\:{for}\:{one} \\ $$$${possible}\:{solution}. \\ $$

Commented by mr W last updated on 05/Sep/22

Commented by mr W last updated on 05/Sep/22

Commented by mr W last updated on 05/Sep/22

Commented by mr W last updated on 05/Sep/22

red curve is the graph of f(f(x)). the seccond case is that what i take.

$${red}\:{curve}\:{is}\:{the}\:{graph}\:{of}\:{f}\left({f}\left({x}\right)\right). \\ $$$${the}\:{seccond}\:{case}\:{is}\:{that}\:{what}\:{i}\:{take}. \\ $$

Commented by mr W last updated on 05/Sep/22

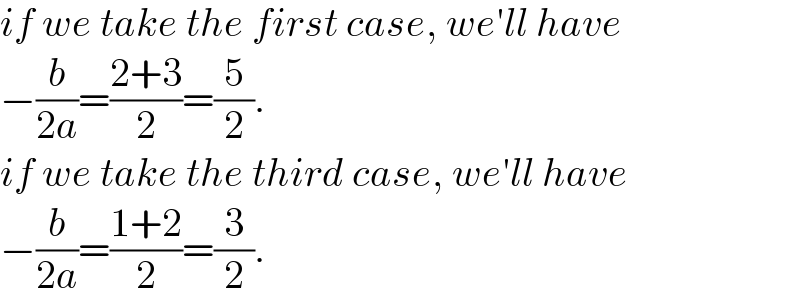
if we take the first case, we′ll have −(b/(2a))=((2+3)/2)=(5/2). if we take the third case, we′ll have −(b/(2a))=((1+2)/2)=(3/2).

$${if}\:{we}\:{take}\:{the}\:{first}\:{case},\:{we}'{ll}\:{have} \\ $$$$−\frac{{b}}{\mathrm{2}{a}}=\frac{\mathrm{2}+\mathrm{3}}{\mathrm{2}}=\frac{\mathrm{5}}{\mathrm{2}}. \\ $$$${if}\:{we}\:{take}\:{the}\:{third}\:{case},\:{we}'{ll}\:{have} \\ $$$$−\frac{{b}}{\mathrm{2}{a}}=\frac{\mathrm{1}+\mathrm{2}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}}. \\ $$

Commented by Rasheed.Sindhi last updated on 05/Sep/22

Thanks a LOT SIR!

$$\mathbb{T}\boldsymbol{\mathrm{han}}\Bbbk\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{LOT}}\:\boldsymbol{\mathcal{S}}\mathcal{IR}! \\ $$

Commented by infinityaction last updated on 05/Sep/22

thanks sir

$${thanks}\:{sir} \\ $$

Commented by Tawa11 last updated on 05/Sep/22

Great sirs.

$$\mathrm{Great}\:\mathrm{sirs}. \\ $$

Answered by mahdipoor last updated on 05/Sep/22

if f(x)=ax^2 +bx+c f(m)=f(n) ⇔ m=n or m+n=e (e=((−b)/a)) ⇒ get {i,j,k}={1,2,3} { ((f(f(i))=f(f(j)) ⇒ f(i)=f(j) I)),((f(f(j))=f(f(k))⇒ f(j)+f(k)=e II)) :} I: i+j=e ⇒ b=−(i+j)a II: f(j)+f(k)=e ⇒ a(j^2 +k^2 )−a(i+j)(j+k)+2c=i+j ⇒ c=(1/2)((i+j)(a(j+k)+1)−a(k^2 +j^2 )) ⇒⇒f(x)=ax^2 −(i+j)ax+ (((i+j)(a(j+k)+1)−a(k^2 +j^2 ))/2) −−−−− (problem have 3 answer ) if (i,j,k)= 1: (1,2,3) or (2,1,3) ⇒ f(x)=ax^2 −3ax+((2a+3)/2) 2: (1,3,2) or (3,1,2) ⇒ f(x)=ax^2 −4ax+((7a+4)/2) 3: (2,3,1) or (3,2,1)⇒ f(x)=ax^2 −5ax+((10a+5)/2)

$${if}\:{f}\left({x}\right)={ax}^{\mathrm{2}} +{bx}+{c}\: \\ $$$${f}\left({m}\right)={f}\left({n}\right)\:\Leftrightarrow\:{m}={n}\:{or}\:\:{m}+{n}={e}\:\:\:\left({e}=\frac{−{b}}{{a}}\right) \\ $$$$\Rightarrow\:{get}\:\:\left\{{i},{j},{k}\right\}=\left\{\mathrm{1},\mathrm{2},\mathrm{3}\right\} \\ $$$$\begin{cases}{{f}\left({f}\left({i}\right)\right)={f}\left({f}\left({j}\right)\right)\:\Rightarrow\:{f}\left({i}\right)={f}\left({j}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:{I}}\\{{f}\left({f}\left({j}\right)\right)={f}\left({f}\left({k}\right)\right)\Rightarrow\:{f}\left({j}\right)+{f}\left({k}\right)={e}\:\:\:\:\:\:{II}}\end{cases}\: \\ $$$${I}:\:{i}+{j}={e}\:\:\:\Rightarrow\:\:\:{b}=−\left({i}+{j}\right){a} \\ $$$${II}:\:{f}\left({j}\right)+{f}\left({k}\right)={e}\:\:\Rightarrow \\ $$$${a}\left({j}^{\mathrm{2}} +{k}^{\mathrm{2}} \right)−{a}\left({i}+{j}\right)\left({j}+{k}\right)+\mathrm{2}{c}={i}+{j}\:\Rightarrow \\ $$$${c}=\frac{\mathrm{1}}{\mathrm{2}}\left(\left({i}+{j}\right)\left({a}\left({j}+{k}\right)+\mathrm{1}\right)−{a}\left({k}^{\mathrm{2}} +{j}^{\mathrm{2}} \right)\right) \\ $$$$\Rightarrow\Rightarrow{f}\left({x}\right)={ax}^{\mathrm{2}} −\left({i}+{j}\right){ax}+ \\ $$$$\frac{\left({i}+{j}\right)\left({a}\left({j}+{k}\right)+\mathrm{1}\right)−{a}\left({k}^{\mathrm{2}} +{j}^{\mathrm{2}} \right)}{\mathrm{2}} \\ $$$$−−−−− \\ $$$$\left({problem}\:{have}\:\mathrm{3}\:{answer}\:\right) \\ $$$${if}\:\left({i},{j},{k}\right)=\: \\ $$$$\mathrm{1}:\:\left(\mathrm{1},\mathrm{2},\mathrm{3}\right)\:{or}\:\left(\mathrm{2},\mathrm{1},\mathrm{3}\right)\:\Rightarrow \\ $$$$\:{f}\left({x}\right)={ax}^{\mathrm{2}} −\mathrm{3}{ax}+\frac{\mathrm{2}{a}+\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{2}:\:\left(\mathrm{1},\mathrm{3},\mathrm{2}\right)\:{or}\:\left(\mathrm{3},\mathrm{1},\mathrm{2}\right)\:\Rightarrow \\ $$$$\:{f}\left({x}\right)={ax}^{\mathrm{2}} −\mathrm{4}{ax}+\frac{\mathrm{7}{a}+\mathrm{4}}{\mathrm{2}} \\ $$$$\mathrm{3}:\:\left(\mathrm{2},\mathrm{3},\mathrm{1}\right)\:{or}\:\left(\mathrm{3},\mathrm{2},\mathrm{1}\right)\Rightarrow\: \\ $$$$\:{f}\left({x}\right)={ax}^{\mathrm{2}} −\mathrm{5}{ax}+\frac{\mathrm{10}{a}+\mathrm{5}}{\mathrm{2}} \\ $$

Commented by mr W last updated on 05/Sep/22

great solution sir!

$${great}\:{solution}\:{sir}! \\ $$

Commented by mahdipoor last updated on 05/Sep/22

♥

$$\heartsuit \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com