
Question Number 175715 by zaheen last updated on 05/Sep/22
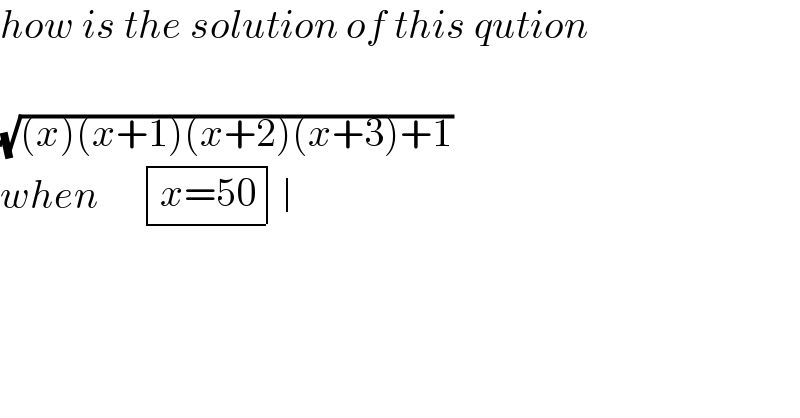
$${how}\:{is}\:{the}\:{solution}\:{of}\:{this}\:{qution} \\ $$$$ \\ $$$$\sqrt{\left({x}\right)\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)\left({x}+\mathrm{3}\right)+\mathrm{1}} \\ $$$${when}\:\:\:\:\:\begin{array}{|c|}{{x}=\mathrm{50}}\\\hline\end{array}\begin{array}{|c|c|}\\\\\hline\end{array} \\ $$
Commented by Frix last updated on 05/Sep/22
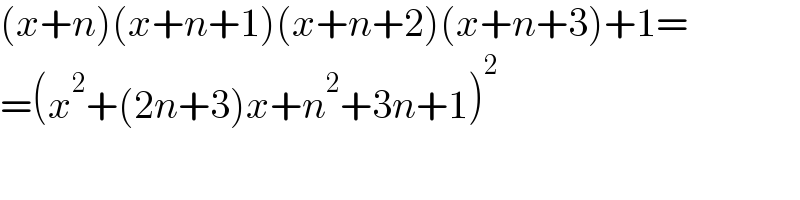
$$\left({x}+{n}\right)\left({x}+{n}+\mathrm{1}\right)\left({x}+{n}+\mathrm{2}\right)\left({x}+{n}+\mathrm{3}\right)+\mathrm{1}= \\ $$$$=\left({x}^{\mathrm{2}} +\left(\mathrm{2}{n}+\mathrm{3}\right){x}+{n}^{\mathrm{2}} +\mathrm{3}{n}+\mathrm{1}\right)^{\mathrm{2}} \\ $$
Answered by ajfour last updated on 05/Sep/22
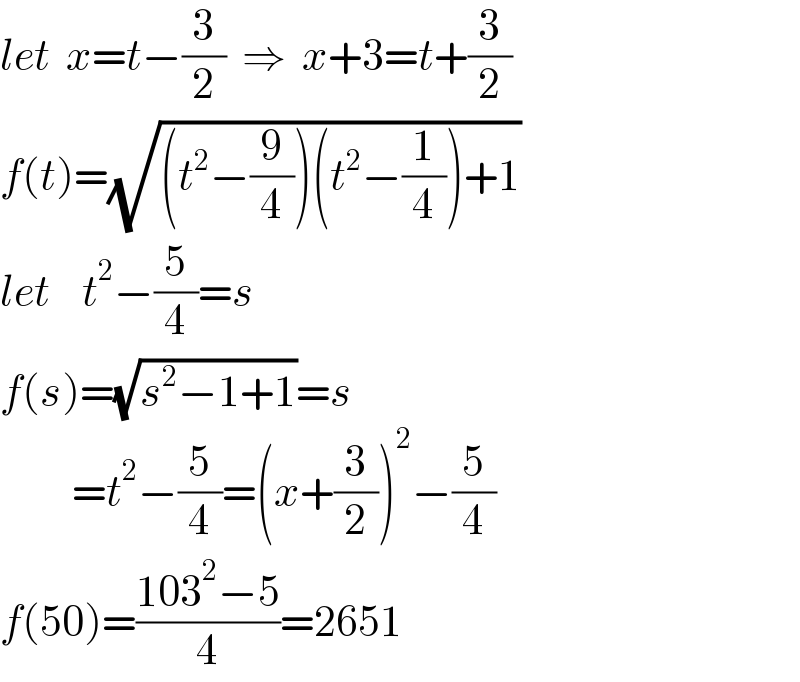
$${let}\:\:{x}={t}−\frac{\mathrm{3}}{\mathrm{2}}\:\:\Rightarrow\:\:{x}+\mathrm{3}={t}+\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${f}\left({t}\right)=\sqrt{\left({t}^{\mathrm{2}} −\frac{\mathrm{9}}{\mathrm{4}}\right)\left({t}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\right)+\mathrm{1}} \\ $$$${let}\:\:\:\:{t}^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{4}}={s} \\ $$$${f}\left({s}\right)=\sqrt{{s}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}={s} \\ $$$$\:\:\:\:\:\:\:\:\:={t}^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{4}}=\left({x}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{4}} \\ $$$${f}\left(\mathrm{50}\right)=\frac{\mathrm{103}^{\mathrm{2}} −\mathrm{5}}{\mathrm{4}}=\mathrm{2651} \\ $$
Commented by Tawa11 last updated on 05/Sep/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by behi834171 last updated on 05/Sep/22
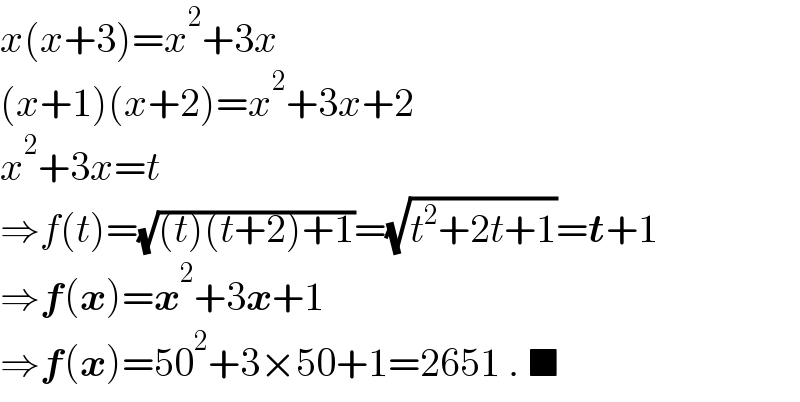
$${x}\left({x}+\mathrm{3}\right)={x}^{\mathrm{2}} +\mathrm{3}{x} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)={x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{2} \\ $$$${x}^{\mathrm{2}} +\mathrm{3}{x}={t} \\ $$$$\Rightarrow{f}\left({t}\right)=\sqrt{\left({t}\right)\left({t}+\mathrm{2}\right)+\mathrm{1}}=\sqrt{{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}}=\boldsymbol{{t}}+\mathrm{1} \\ $$$$\Rightarrow\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)=\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{3}\boldsymbol{{x}}+\mathrm{1} \\ $$$$\Rightarrow\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)=\mathrm{50}^{\mathrm{2}} +\mathrm{3}×\mathrm{50}+\mathrm{1}=\mathrm{2651}\:.\:\blacksquare \\ $$
