Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 66019 by Rio Michael last updated on 07/Aug/19

lim_(x→∞) (1 + (2/x))^x =

$$\underset{{x}\rightarrow\infty} {{lim}}\:\left(\mathrm{1}\:+\:\frac{\mathrm{2}}{{x}}\right)^{{x}} \:= \\ $$

Commented by mathmax by abdo last updated on 07/Aug/19

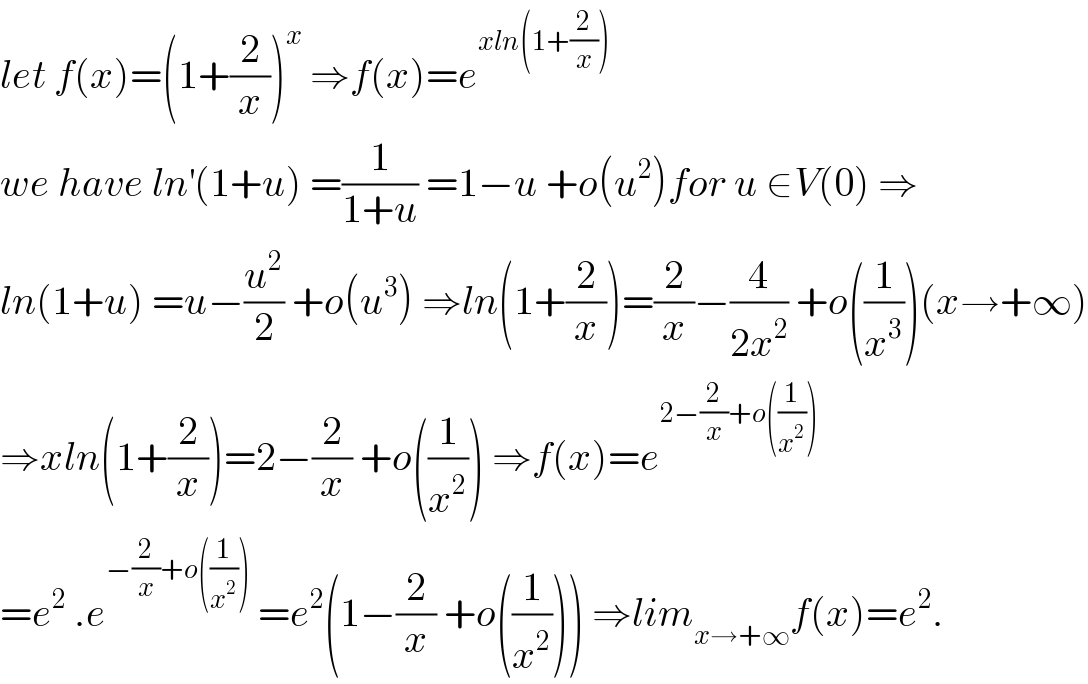
let f(x)=(1+(2/x))^x ⇒f(x)=e^(xln(1+(2/x))) we have ln^′ (1+u) =(1/(1+u)) =1−u +o(u^2 )for u ∈V(0) ⇒ ln(1+u) =u−(u^2 /2) +o(u^3 ) ⇒ln(1+(2/x))=(2/x)−(4/(2x^2 )) +o((1/x^3 ))(x→+∞) ⇒xln(1+(2/x))=2−(2/x) +o((1/x^2 )) ⇒f(x)=e^(2−(2/x)+o((1/x^2 ))) =e^2 .e^(−(2/x)+o((1/x^2 ))) =e^2 (1−(2/x) +o((1/x^2 ))) ⇒lim_(x→+∞) f(x)=e^2 .

$${let}\:{f}\left({x}\right)=\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)^{{x}} \:\Rightarrow{f}\left({x}\right)={e}^{{xln}\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)} \\ $$$${we}\:{have}\:{ln}^{'} \left(\mathrm{1}+{u}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+{u}}\:=\mathrm{1}−{u}\:+{o}\left({u}^{\mathrm{2}} \right){for}\:{u}\:\in{V}\left(\mathrm{0}\right)\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{u}\right)\:={u}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\:+{o}\left({u}^{\mathrm{3}} \right)\:\Rightarrow{ln}\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)=\frac{\mathrm{2}}{{x}}−\frac{\mathrm{4}}{\mathrm{2}{x}^{\mathrm{2}} }\:+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)\left({x}\rightarrow+\infty\right) \\ $$$$\Rightarrow{xln}\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)=\mathrm{2}−\frac{\mathrm{2}}{{x}}\:+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\:\Rightarrow{f}\left({x}\right)={e}^{\mathrm{2}−\frac{\mathrm{2}}{{x}}+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)} \\ $$$$={e}^{\mathrm{2}} \:.{e}^{−\frac{\mathrm{2}}{{x}}+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)} \:={e}^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{2}}{{x}}\:+{o}\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\right)\:\Rightarrow{lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)={e}^{\mathrm{2}} . \\ $$

Answered by Tanmay chaudhury last updated on 07/Aug/19

t=lim_(x→∞) (1+(2/x))^x y=(1/x) as x→∞ y→0 t=lim_(y→0) (1+2y)^(1/y) lnt=lim_(y→0) ((ln(1+2y))/(2y))×2 lnt=1×2 [formula lim_(x→0) ((ln(1+x))/x)=1] t=e^2 answer

$${t}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)^{{x}} \\ $$$${y}=\frac{\mathrm{1}}{{x}}\:\:\:{as}\:{x}\rightarrow\infty\:\:\:{y}\rightarrow\mathrm{0} \\ $$$${t}=\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{1}+\mathrm{2}{y}\right)^{\frac{\mathrm{1}}{{y}}} \\ $$$${lnt}=\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{ln}\left(\mathrm{1}+\mathrm{2}{y}\right)}{\mathrm{2}{y}}×\mathrm{2} \\ $$$${lnt}=\mathrm{1}×\mathrm{2}\:\:\:\left[{formula}\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}=\mathrm{1}\right] \\ $$$${t}={e}^{\mathrm{2}} \:\:{answer} \\ $$

Answered by kaivan.ahmadi last updated on 07/Aug/19

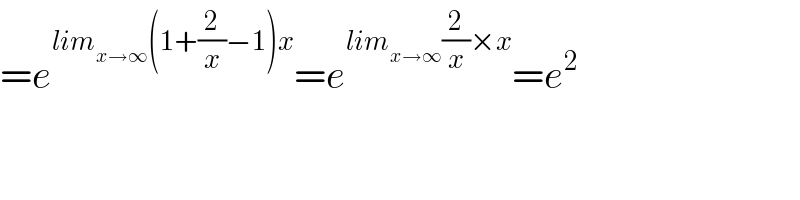
=e^(lim_(x→∞) (1+(2/x)−1)x) =e^(lim_(x→∞) (2/x)×x) =e^2

$$={e}^{{lim}_{{x}\rightarrow\infty} \left(\mathrm{1}+\frac{\mathrm{2}}{{x}}−\mathrm{1}\right){x}} ={e}^{{lim}_{{x}\rightarrow\infty} \frac{\mathrm{2}}{{x}}×{x}} ={e}^{\mathrm{2}} \\ $$

Commented by Rio Michael last updated on 07/Aug/19

please guys check my solution as i understand it. lim_(x→∞) (1 +(2/x))^x let (2/x) = (1/m) ⇒ x =2m such that x →∞ , m →∞ lim_(m→∞) [(1 + (1/m))^m ]^2 = e^2

$${please}\:{guys}\:{check}\:{my}\:{solution}\:{as}\:{i}\:{understand}\:{it}. \\ $$$$\:\underset{{x}\rightarrow\infty} {{lim}}\:\left(\mathrm{1}\:+\frac{\mathrm{2}}{{x}}\right)^{{x}} \\ $$$${let}\:\:\frac{\mathrm{2}}{{x}}\:=\:\frac{\mathrm{1}}{{m}} \\ $$$$\Rightarrow\:{x}\:=\mathrm{2}{m} \\ $$$${such}\:{that}\:\:{x}\:\rightarrow\infty\:,\:{m}\:\rightarrow\infty \\ $$$$\underset{{m}\rightarrow\infty} {{lim}}\left[\left(\mathrm{1}\:+\:\frac{\mathrm{1}}{{m}}\right)^{{m}} \right]^{\mathrm{2}} \\ $$$$\:=\:{e}^{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com