
Question Number 175766 by BaliramKumar last updated on 06/Sep/22

$${Number}\:{of}\:\:{even}\:{composite}\:{factors}\:{of}\:\mathrm{2520}? \\ $$
Commented by mr W last updated on 06/Sep/22

$$\mathrm{2520}=\mathrm{2}^{\mathrm{3}} ×\mathrm{3}^{\mathrm{2}} ×\mathrm{5}×\mathrm{7} \\ $$$${for}\:{even}\:{factors}\:\mathrm{2}\:{must}\:{be}\:{contained} \\ $$$${at}\:{least}\:{one}\:{time},\:\mathrm{2520}\:{must}\:{be}\:{excluded}. \\ $$$$\Rightarrow\mathrm{3}×\mathrm{3}×\mathrm{2}×\mathrm{2}−\mathrm{1}=\mathrm{35} \\ $$
Answered by aleks041103 last updated on 06/Sep/22
![let s(n) be the number of composite factors of n. let n=p_1 ^r_1 p_2 ^r_2 ...p_k ^r_k , where p_(1,2,..,k) are primes and r_(1,2,...,k) ∈N={1,2,...} any factor f of n must be of the form: f=p_1 ^t_1 p_2 ^t_2 ...p_k ^t_k , where 0≤t_i ≤r_i . ⇒ for t_i we have r_i +1 possibilities. ⇒#factors of n=Π_(i=1) ^k (1+r_i )=σ(n) out of those σ(n) factors the noncomposite are 1,p_1 ,p_2 ,...,p_k , i.e. k+1. ⇒s(n)=σ(n)−k−1 ⇒s(n)=[Π_(i=1) ^k (1+r_i )]−k−1 Now, the composite factors are 2 types devisible by p_q and not devisible by p_q . The ones not devisible by p_q are all the composite factors of (n/p_q ^r_q ) ⇒The answer is: s(n)−s((n/p_q ^r_q ))= { (([r_q Π_(i=1,i≠q) ^k (1+r_i )]−1 , p_q ∣n)),(([r_q Π_(i=1,i≠q) ^k (1+r_i )] , p_q ∤n)) :} in our case: 2520=2.5.2.2.7.9=2^3 .3^2 .5.7 ⇒ ans.=3(2+1)(1+1)(1+1)−1= =3.3.2.2−1=35 ⇒Ans. 35](Q175771.png)
$${let}\:{s}\left({n}\right)\:{be}\:{the}\:{number}\:{of}\:{composite}\:{factors} \\ $$$${of}\:{n}. \\ $$$${let}\:{n}={p}_{\mathrm{1}} ^{{r}_{\mathrm{1}} } {p}_{\mathrm{2}} ^{{r}_{\mathrm{2}} } ...{p}_{{k}} ^{{r}_{{k}} } ,\:{where}\:{p}_{\mathrm{1},\mathrm{2},..,{k}} \:{are}\:{primes} \\ $$$${and}\:{r}_{\mathrm{1},\mathrm{2},...,{k}} \in\mathbb{N}=\left\{\mathrm{1},\mathrm{2},...\right\} \\ $$$${any}\:{factor}\:{f}\:{of}\:{n}\:{must}\:{be}\:{of}\:{the}\:{form}: \\ $$$${f}={p}_{\mathrm{1}} ^{{t}_{\mathrm{1}} } {p}_{\mathrm{2}} ^{{t}_{\mathrm{2}} } ...{p}_{{k}} ^{{t}_{{k}} } ,\:{where}\:\mathrm{0}\leqslant{t}_{{i}} \leqslant{r}_{{i}} . \\ $$$$\Rightarrow\:{for}\:{t}_{{i}} \:{we}\:{have}\:{r}_{{i}} +\mathrm{1}\:{possibilities}. \\ $$$$\Rightarrow#{factors}\:{of}\:{n}=\underset{{i}=\mathrm{1}} {\overset{{k}} {\prod}}\left(\mathrm{1}+{r}_{{i}} \right)=\sigma\left({n}\right) \\ $$$${out}\:{of}\:{those}\:\sigma\left({n}\right)\:{factors}\:{the}\:{noncomposite} \\ $$$${are}\:\mathrm{1},{p}_{\mathrm{1}} ,{p}_{\mathrm{2}} ,...,{p}_{{k}} ,\:{i}.{e}.\:{k}+\mathrm{1}. \\ $$$$\Rightarrow{s}\left({n}\right)=\sigma\left({n}\right)−{k}−\mathrm{1} \\ $$$$\Rightarrow{s}\left({n}\right)=\left[\underset{{i}=\mathrm{1}} {\overset{{k}} {\prod}}\left(\mathrm{1}+{r}_{{i}} \right)\right]−{k}−\mathrm{1} \\ $$$${Now},\:{the}\:{composite}\:{factors}\:{are}\:\mathrm{2}\:{types} \\ $$$${devisible}\:{by}\:{p}_{{q}} \:{and}\:{not}\:{devisible}\:{by}\:{p}_{{q}} . \\ $$$${The}\:{ones}\:{not}\:{devisible}\:{by}\:{p}_{{q}} \:{are}\:{all}\:{the}\: \\ $$$${composite}\:{factors}\:{of}\:\:\frac{{n}}{{p}_{{q}} ^{{r}_{{q}} } } \\ $$$$\Rightarrow{The}\:{answer}\:{is}: \\ $$$${s}\left({n}\right)−{s}\left(\frac{{n}}{{p}_{{q}} ^{{r}_{{q}} } }\right)=\begin{cases}{\left[{r}_{{q}} \underset{{i}=\mathrm{1},{i}\neq{q}} {\overset{{k}} {\prod}}\left(\mathrm{1}+{r}_{{i}} \right)\right]−\mathrm{1}\:,\:{p}_{{q}} \mid{n}}\\{\left[{r}_{{q}} \underset{{i}=\mathrm{1},{i}\neq{q}} {\overset{{k}} {\prod}}\left(\mathrm{1}+{r}_{{i}} \right)\right]\:,\:{p}_{{q}} \nmid{n}}\end{cases} \\ $$$${in}\:{our}\:{case}: \\ $$$$\mathrm{2520}=\mathrm{2}.\mathrm{5}.\mathrm{2}.\mathrm{2}.\mathrm{7}.\mathrm{9}=\mathrm{2}^{\mathrm{3}} .\mathrm{3}^{\mathrm{2}} .\mathrm{5}.\mathrm{7} \\ $$$$\Rightarrow\:{ans}.=\mathrm{3}\left(\mathrm{2}+\mathrm{1}\right)\left(\mathrm{1}+\mathrm{1}\right)\left(\mathrm{1}+\mathrm{1}\right)−\mathrm{1}= \\ $$$$=\mathrm{3}.\mathrm{3}.\mathrm{2}.\mathrm{2}−\mathrm{1}=\mathrm{35} \\ $$$$\Rightarrow{Ans}.\:\mathrm{35} \\ $$
Commented by aleks041103 last updated on 06/Sep/22

Commented by mr W last updated on 06/Sep/22
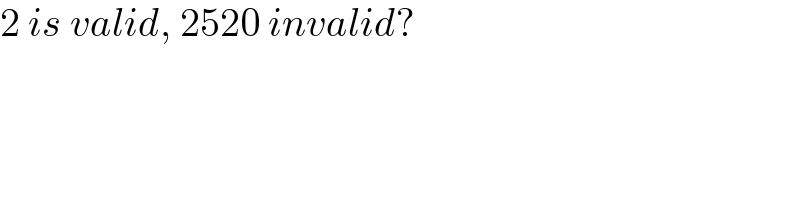
$$\mathrm{2}\:{is}\:{valid},\:\mathrm{2520}\:{invalid}? \\ $$
Commented by BaliramKumar last updated on 06/Sep/22

$${thanks} \\ $$
Commented by aleks041103 last updated on 07/Sep/22

$${Well}\:\mathrm{2}\:{is}\:{even}\:{but}\:{not}\:{composite},\:{while} \\ $$$$\mathrm{2520}\:{is}\:{both}\:{even}\:{and}\:{composite}\:{and}\:{also} \\ $$$${is}\:{a}\:{factor}\:{of}\:{itself}. \\ $$$${So}\:\mathrm{2}\:{doesn}'{t}\:{count},\:{while}\:\mathrm{2520}\:{counts}. \\ $$
