Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 175987 by stelor last updated on 10/Sep/22

$$pleasecalculate$$$$I={\int }_0^{\frac{\pi }{2}}\frac{dx}{1+{\left(tanx\right)}^{\sqrt{2}}}$$$$J={\int }_0^{\pi }\frac{dx}{a^2{cos}^{2}x+{sin}^{2}x}$$$$K={\int }_0^{\frac{\pi }{2}}\frac{dx}{3tanx+2}$$

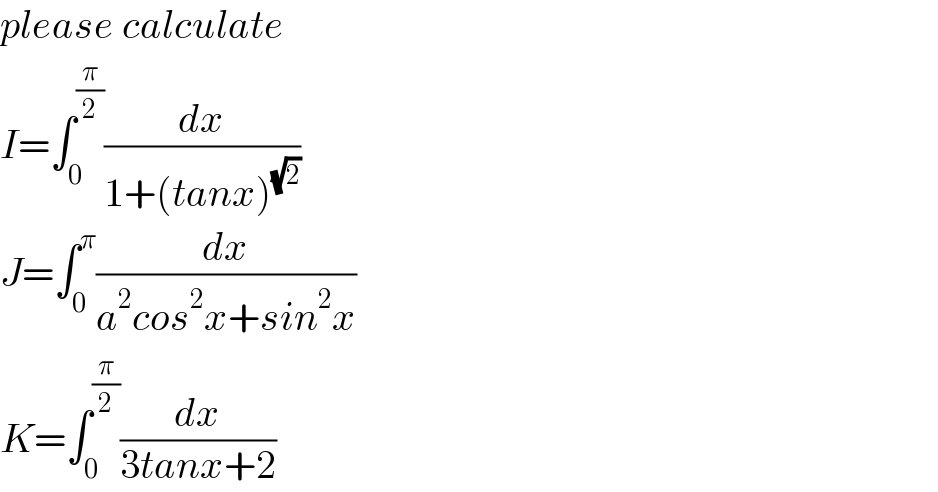
Answered by Ar Brandon last updated on 10/Sep/22

$$J={\int }_0^{\pi }\frac{dx}{a^2{\cos }^{2}x+{\sin }^{2}x}={\int }_0^{\pi }\frac{{\sec }^{2}x}{a^2+{\tan }^{2}x}dx$$$$=2{\int }_0^{\frac{\pi }{2}}\frac{d\left(\tan x\right)}{a^2+{\tan }^{2}x}=\frac{2}{a}{\left[\arctan \left(\frac{\tan x}{a}\right)\right]}_0^{\frac{\pi }{2}}=\frac{\pi }{a}$$

Commented by stelor last updated on 10/Sep/22

$$Thanks$$

Answered by Ar Brandon last updated on 10/Sep/22

$$I={\int }_0^{\frac{\pi }{2}}\frac{dx}{1+{\left(\tan x\right)}^{\sqrt{2}}}={\int }_0^{\frac{\pi }{2}}\frac{{\left(\cos x\right)}^{\sqrt{2}}}{{\left(\sin x\right)}^{\sqrt{2}}+{\left(\cos x\right)}^{\sqrt{2}}}dx...\left(i\right)$$$$I={\int }_0^{\frac{\pi }{2}}\frac{{\left(\sin x\right)}^{\sqrt{2}}}{{\left(\sin x\right)}^{\sqrt{2}}+{\left(\cos x\right)}^{\sqrt{2}}}dx...\left(ii\right)$$$$\left(i\right)+\left(ii\right)\Rightarrow$$$$2I={\int }_0^{\frac{\pi }{2}}\frac{{\left(\sin x\right)}^{\sqrt{2}}+{\left(\cos x\right)}^{\sqrt{2}}}{{\left(\sin x\right)}^{\sqrt{2}}+{\left(\cos x\right)}^{\sqrt{2}}}dx=\frac{\pi }{2}$$$$\Rightarrow I=\frac{\pi }{4}$$

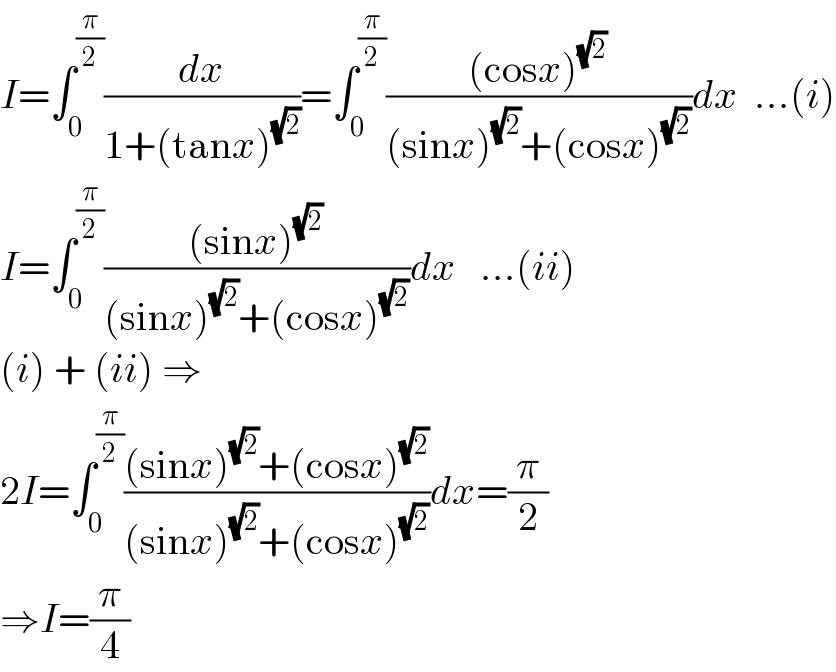
Answered by Ar Brandon last updated on 10/Sep/22

Commented by Ar Brandon last updated on 10/Sep/22

$$K\approx 0,335236$$

Commented by Ar Brandon last updated on 11/Sep/22

$$K={\int }_0^{\frac{\pi }{2}}\frac{dx}{3\tan x+2}={\int }_0^1\frac{2}{3\left(\frac{2t}{1-t^2}\right)+2}\cdot \frac{dt}{1+t^2}={\int }_0^1\frac{t^2-1}{2t^2-6t-2}\cdot \frac{2dt}{t^2+1}$$$$={\int }_0^1\frac{t^2-1}{(t^2-3t-1)(t^2+1)}dt=\frac{1}{13}{\int }_0^1(\frac{6t-9}{t^2-3t-1}-\frac{6t-4}{t^2+1})dt$$$$---------------------------$$$$\frac{at+b}{t^2-3t-1}+\frac{ct+d}{t^2+1}=\frac{(at+b)(t^2+1)+(ct+d)(t^2-3t-1)}{(t^2-3t-1)(t^2+1)}$$$$a+c\stackrel{t^3}{=}0,b-3c+d=1,a-c-3d=0,b-d=-1$$$$\underset{t\to i}{\lim }\Rightarrow (ci+d)(-2-3i)=(-2d+3c)-i(2c+3d)=-2$$$$\Rightarrow c=-\frac{6}{13},d=\frac{4}{13},\Rightarrow b=-\frac{9}{13},a=\frac{6}{13}$$$$---------------------------$$$$=\frac{1}{13}{\int }_0^1\frac{3(2t-3)}{t^2-3t-1}dt-\frac{3}{13}{\int }_0^1\frac{2t}{t^2+1}dt+\frac{4}{13}{\int }_0^1\frac{1}{t^2+1}dt$$$$=\frac{3}{13}{[\ln \mid t^2-3t-1\mid ]}_0^1-\frac{3}{13}{\left[\ln (t^2+1)\right]}_0^1+\frac{4}{13}{\left[\arctan \left(t\right)\right]}_0^1$$$$=\frac{3}{13}{[\ln \mid \frac{t^2-3t-1}{t^2+1}\mid ]}_0^1+\frac{4}{13}\left(\frac{\pi }{4}\right)=\frac{1}{13}\ln {\left(\frac{3}{2}\right)}^3+\frac{\pi }{13}$$$$=\frac{1}{13}\ln \left(\frac{27}{8}\right)+\frac{\pi }{13}=\frac{1}{13}(\pi +\ln \left(\frac{27}{8}\right))\approx 0,33523$$

Answered by a.lgnaoui last updated on 10/Sep/22

$$$$$$k={\int }_0^{\frac{\pi }{2}}\frac{dx}{3tanx+2}posonst=tanxx=arctant$$$$dt=(1+t^2)dxdx=\frac{dt}{1+t^2}$$$$k={\int }_0^{\mathrm{\infty }}\frac{dt}{(3t+2)(1+t^2)}={\int }_0^{\mathrm{\infty }}(\frac{-3t+2}{13(1+t^2)}+\frac{9}{13(3t+2)})dt$$$$=-\frac{3}{26}\int \frac{2t-\frac{2}{3}}{1+t^2}dt+\frac{9}{13}\int \frac{dt}{3t+2}$$$$=-\frac{3}{26}{\left[\log (1+{\mathrm{t}}^2)\right]}_0^{\mathrm{\infty }}+\frac{1}{13}{\int }_0^{\mathrm{\infty }}\frac{dt}{1+t^2}+\frac{9}{13}{\left[\log (3\mathrm{t}+2)\right]}_0^{\mathrm{\infty }}$$$$=\frac{-3}{26}{\left[\log (1+{\mathrm{t}}^2)\right]}_0^{\mathrm{\infty }}+\frac{1}{13}{\left[arctan\left(t\right)\right]}_0^{\mathrm{\infty }}+\frac{9}{13}{\left[\log (3\mathrm{t}+2)\right]}_0^{\mathrm{\infty }}$$$$$$$$\frac{-1}{13}{\left[\log (1+{\mathrm{t}}^2)\right]}_0^{\mathrm{\infty }}+\frac{9}{13}{\left[\log (3\mathrm{t}+2)\right]}_0^{\mathrm{\infty }}+\frac{\pi }{26}$$$$=\log {\left[\left(\frac{{(3\mathrm{t}+2)}^{\frac{9}{13}}}{{(1+{\mathrm{t}}^2)}^{\frac{1}{13}}}\right)\right]}_0^{\mathrm{\infty }}+\frac{\pi }{26}$$$$\mathrm{t}=0\frac{{(3\mathrm{t}+2)}^{\frac{9}{13}}}{{(1+\mathrm{t})}^{\frac{1}{13}}}=2^{\frac{9}{13}}$$$$t\to \mathrm{\infty }\frac{3t^{\frac{9}{13}}{(1+\frac{2}{t})}^{\frac{9}{13}}}{t^{\frac{1}{13}}{(1+\frac{1}{t})}^{\frac{1}{13}}}=3^{\frac{9}{13}}{t}^{\frac{8}{13}}$$$$k=\frac{9}{13}\log \left(\frac{3}{2}\right)+\frac{\pi }{26}+\frac{8}{13}{\lim }_{\mathrm{t}\to \mathrm{\infty }}\left(\mathrm{logt}\right)$$$$k=+\mathrm{\infty }$$$$$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com