
Question Number 17604 by tawa tawa last updated on 08/Jul/17
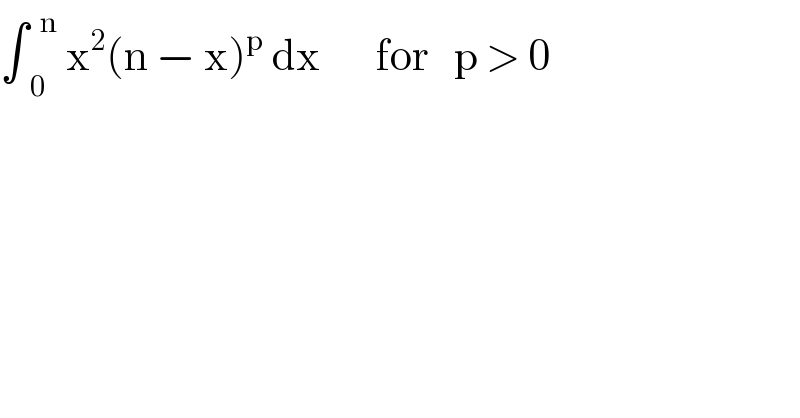
$$\int_{\:\:\mathrm{0}} ^{\:\:\mathrm{n}} \:\mathrm{x}^{\mathrm{2}} \left(\mathrm{n}\:−\:\mathrm{x}\right)^{\mathrm{p}} \:\mathrm{dx}\:\:\:\:\:\:\:\mathrm{for}\:\:\:\mathrm{p}\:>\:\mathrm{0} \\ $$
Answered by sma3l2996 last updated on 08/Jul/17
![t=n−x⇒dt=−dx I=∫_0 ^n x^2 (n−x)^p dx=∫_0 ^n (n−t)^2 t^p dt=∫_0 ^n (n^2 t^p −2nt^(p+1) +t^(p+2) )dt =[(n^2 /(p+1))t^(p+1) −((2n)/(p+2))t^(p+2) +(t^(p+3) /(p+3))]_0 ^n =(n^2 /(p+1))n^(p+1) −((2n)/(p+2))n^(p+2) +(n^(p+3) /(p+3)) =n^(p+3) ((1/(p+1))−(2/(p+2))+(1/(p+3)))=n^(p+3) ((((p+3)(p+2)−2(p+1)(p+3)+(p+1)(p+2))/((p+1)(p+2)(p+3)))) =n^(p+3) (((p^2 +5p+6−2p^2 −8p−6+p^2 +3p+2)/((p+1)(p+2)(p+3)))) I=((2n^(p+3) )/((p+1)(p+2)(p+3)))](Q17606.png)
$${t}={n}−{x}\Rightarrow{dt}=−{dx} \\ $$ $${I}=\int_{\mathrm{0}} ^{{n}} {x}^{\mathrm{2}} \left({n}−{x}\right)^{{p}} {dx}=\int_{\mathrm{0}} ^{{n}} \left({n}−{t}\right)^{\mathrm{2}} {t}^{{p}} {dt}=\int_{\mathrm{0}} ^{{n}} \left({n}^{\mathrm{2}} {t}^{{p}} −\mathrm{2}{nt}^{{p}+\mathrm{1}} +{t}^{{p}+\mathrm{2}} \right){dt} \\ $$ $$=\left[\frac{{n}^{\mathrm{2}} }{{p}+\mathrm{1}}{t}^{{p}+\mathrm{1}} −\frac{\mathrm{2}{n}}{{p}+\mathrm{2}}{t}^{{p}+\mathrm{2}} +\frac{{t}^{{p}+\mathrm{3}} }{{p}+\mathrm{3}}\right]_{\mathrm{0}} ^{{n}} \\ $$ $$=\frac{{n}^{\mathrm{2}} }{{p}+\mathrm{1}}{n}^{{p}+\mathrm{1}} −\frac{\mathrm{2}{n}}{{p}+\mathrm{2}}{n}^{{p}+\mathrm{2}} +\frac{{n}^{{p}+\mathrm{3}} }{{p}+\mathrm{3}} \\ $$ $$={n}^{{p}+\mathrm{3}} \left(\frac{\mathrm{1}}{{p}+\mathrm{1}}−\frac{\mathrm{2}}{{p}+\mathrm{2}}+\frac{\mathrm{1}}{{p}+\mathrm{3}}\right)={n}^{{p}+\mathrm{3}} \left(\frac{\left({p}+\mathrm{3}\right)\left({p}+\mathrm{2}\right)−\mathrm{2}\left({p}+\mathrm{1}\right)\left({p}+\mathrm{3}\right)+\left({p}+\mathrm{1}\right)\left({p}+\mathrm{2}\right)}{\left({p}+\mathrm{1}\right)\left({p}+\mathrm{2}\right)\left({p}+\mathrm{3}\right)}\right) \\ $$ $$={n}^{{p}+\mathrm{3}} \left(\frac{{p}^{\mathrm{2}} +\mathrm{5}{p}+\mathrm{6}−\mathrm{2}{p}^{\mathrm{2}} −\mathrm{8}{p}−\mathrm{6}+{p}^{\mathrm{2}} +\mathrm{3}{p}+\mathrm{2}}{\left({p}+\mathrm{1}\right)\left({p}+\mathrm{2}\right)\left({p}+\mathrm{3}\right)}\right) \\ $$ $${I}=\frac{\mathrm{2}{n}^{{p}+\mathrm{3}} }{\left({p}+\mathrm{1}\right)\left({p}+\mathrm{2}\right)\left({p}+\mathrm{3}\right)}\: \\ $$
Commented bytawa tawa last updated on 08/Jul/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by alex041103 last updated on 08/Jul/17

$$\mathrm{We}\:\mathrm{use}\:\mathrm{the}\:\mathrm{substitution}\: \\ $$ $${u}={n}−{x}\Rightarrow−{du}={dx}\:\mathrm{and}\:{x}^{\mathrm{2}} \:=\:\left({n}−{u}\right)^{\mathrm{2}} \\ $$ $$\mathrm{And}\:\mathrm{we}\:\mathrm{change}\:\mathrm{the}\:\mathrm{limits}\:\mathrm{of}\:\mathrm{integration} \\ $$ $${x}=\mathrm{0}\:\:\:\:{x}={n} \\ $$ $${u}={n}\:\:\:\:{u}=\mathrm{0} \\ $$ $$\Rightarrow\underset{\mathrm{0}} {\overset{{n}} {\int}}\:{x}^{\mathrm{2}} \left({n}−{x}\right)^{{p}} \:{dx}\:=\:−\underset{{n}} {\overset{\mathrm{0}} {\int}}\left({n}−{u}\right)^{\mathrm{2}} {u}^{{p}} \:{du} \\ $$ $$=\underset{\mathrm{0}} {\overset{{n}} {\int}}\:\left({n}^{\mathrm{2}} −\mathrm{2}{nu}+{u}^{\mathrm{2}} \right){u}^{{p}} \:{du} \\ $$ $$={n}^{\mathrm{2}} \underset{\mathrm{0}} {\overset{{n}} {\int}}{u}^{{p}} {du}\:−\:\mathrm{2}{n}\underset{\mathrm{0}} {\overset{{n}} {\int}}{u}^{{p}+\mathrm{1}} \:{du}\:+\:\underset{\mathrm{0}} {\overset{{n}} {\int}}{u}^{{p}+\mathrm{2}} \:{du} \\ $$ $$={n}^{\mathrm{2}} \:\frac{{n}^{{p}+\mathrm{1}} −\mathrm{0}}{{p}+\mathrm{1}}\:−\:\mathrm{2}{n}\frac{{n}^{{p}+\mathrm{2}} −\mathrm{0}}{{p}+\mathrm{2}}+\frac{{n}^{{p}+\mathrm{3}} −\mathrm{0}}{{p}+\mathrm{3}} \\ $$ $$=\frac{{n}^{{p}+\mathrm{3}} }{{p}+\mathrm{1}}−\mathrm{2}\frac{{n}^{{p}+\mathrm{3}} }{{p}+\mathrm{2}}+\frac{{n}^{{p}+\mathrm{3}} }{{p}+\mathrm{3}} \\ $$ $$={n}^{{p}+\mathrm{3}} \left(\frac{\mathrm{1}}{{p}+\mathrm{1}}−\frac{\mathrm{2}}{{p}+\mathrm{2}}+\frac{\mathrm{1}}{{p}+\mathrm{3}}\right) \\ $$ $$\mathrm{This}\:\mathrm{can}\:\mathrm{be}\:\mathrm{expressed}\:\mathrm{as} \\ $$ $$\underset{\mathrm{0}} {\overset{{n}} {\int}}\:{x}^{\mathrm{2}} \left({n}−{x}\right)^{{p}} \:{dx}\:=\:\frac{\mathrm{2}{n}^{{p}+\mathrm{3}} }{\left({p}+\mathrm{1}\right)\left({p}+\mathrm{2}\right)\left({p}+\mathrm{3}\right)} \\ $$
Commented bytawa tawa last updated on 08/Jul/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
