Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 176102 by MathsFan last updated on 12/Sep/22

Prove that 4n<2^n for all n≥5

$$\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{Prove}}\:\boldsymbol{\mathrm{that}}\: \\ $$ $$\:\:\:\:\:\mathrm{4}\boldsymbol{\mathrm{n}}<\mathrm{2}^{\boldsymbol{\mathrm{n}}} \:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{all}}\:\boldsymbol{\mathrm{n}}\geqslant\mathrm{5} \\ $$

Answered by a.lgnaoui last updated on 12/Sep/22

n=5 2^5 =32 4×5=20<32 n=6 2^6 =64 4×6=24<64 n=7 2^7 =128 4×7=28<128 ........................... n+1 2^(n+1) 4(n+1)=4n+4<2^n +4 n[4(n+1)]<n(2^n +4)<n(2×2^n )<n2^(n+1) donc 4(n+1)<2^(n+1) n est vrai pour tout n≥5 (n∈ N)

$${n}=\mathrm{5}\:\:\:\mathrm{2}^{\mathrm{5}} =\mathrm{32}\:\:\:\:\:\:\:\:\:\mathrm{4}×\mathrm{5}=\mathrm{20}<\mathrm{32} \\ $$ $${n}=\mathrm{6}\:\:\:\mathrm{2}^{\mathrm{6}} =\mathrm{64}\:\:\:\:\:\:\:\:\:\mathrm{4}×\mathrm{6}=\mathrm{24}<\mathrm{64} \\ $$ $${n}=\mathrm{7}\:\:\:\:\mathrm{2}^{\mathrm{7}} =\mathrm{128}\:\:\:\:\:\:\mathrm{4}×\mathrm{7}=\mathrm{28}<\mathrm{128} \\ $$ $$........................... \\ $$ $${n}+\mathrm{1}\:\:\:\:\:\mathrm{2}^{{n}+\mathrm{1}} \:\:\:\:\:\:\:\:\:\:\mathrm{4}\left({n}+\mathrm{1}\right)=\mathrm{4}{n}+\mathrm{4}<\mathrm{2}^{{n}} +\mathrm{4} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{n}\left[\mathrm{4}\left({n}+\mathrm{1}\right)\right]<{n}\left(\mathrm{2}^{{n}} +\mathrm{4}\right)<{n}\left(\mathrm{2}×\mathrm{2}^{{n}} \right)<{n}\mathrm{2}^{{n}+\mathrm{1}} \\ $$ $${donc}\:\:\:\mathrm{4}\left({n}+\mathrm{1}\right)<\mathrm{2}^{{n}+\mathrm{1}} \\ $$ $${n}\:{est}\:{vrai}\:{pour}\:{tout}\:{n}\geqslant\mathrm{5}\:\left({n}\in\:\mathbb{N}\right) \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

Commented byMathsFan last updated on 13/Sep/22

Merci Monsieur

$$ \\ $$ Merci Monsieur \\n

Answered by mahdipoor last updated on 12/Sep/22

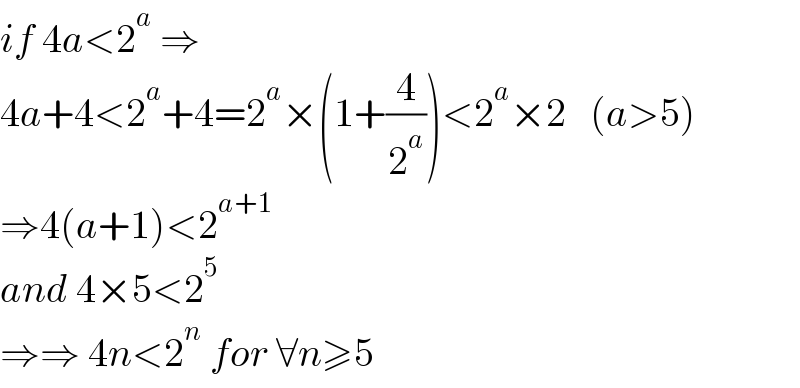
if 4a<2^a ⇒ 4a+4<2^a +4=2^a ×(1+(4/2^a ))<2^a ×2 (a>5) ⇒4(a+1)<2^(a+1) and 4×5<2^5 ⇒⇒ 4n<2^n for ∀n≥5

$${if}\:\mathrm{4}{a}<\mathrm{2}^{{a}} \:\Rightarrow \\ $$ $$\mathrm{4}{a}+\mathrm{4}<\mathrm{2}^{{a}} +\mathrm{4}=\mathrm{2}^{{a}} ×\left(\mathrm{1}+\frac{\mathrm{4}}{\mathrm{2}^{{a}} }\right)<\mathrm{2}^{{a}} ×\mathrm{2}\:\:\:\left({a}>\mathrm{5}\right) \\ $$ $$\Rightarrow\mathrm{4}\left({a}+\mathrm{1}\right)<\mathrm{2}^{{a}+\mathrm{1}} \:\: \\ $$ $${and}\:\mathrm{4}×\mathrm{5}<\mathrm{2}^{\mathrm{5}} \\ $$ $$\Rightarrow\Rightarrow\:\mathrm{4}{n}<\mathrm{2}^{{n}} \:{for}\:\forall{n}\geqslant\mathrm{5} \\ $$

Commented byMathsFan last updated on 13/Sep/22

thank you sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com