
Question and Answers Forum
Question Number 176199 by infinityaction last updated on 14/Sep/22

Answered by mr W last updated on 15/Sep/22
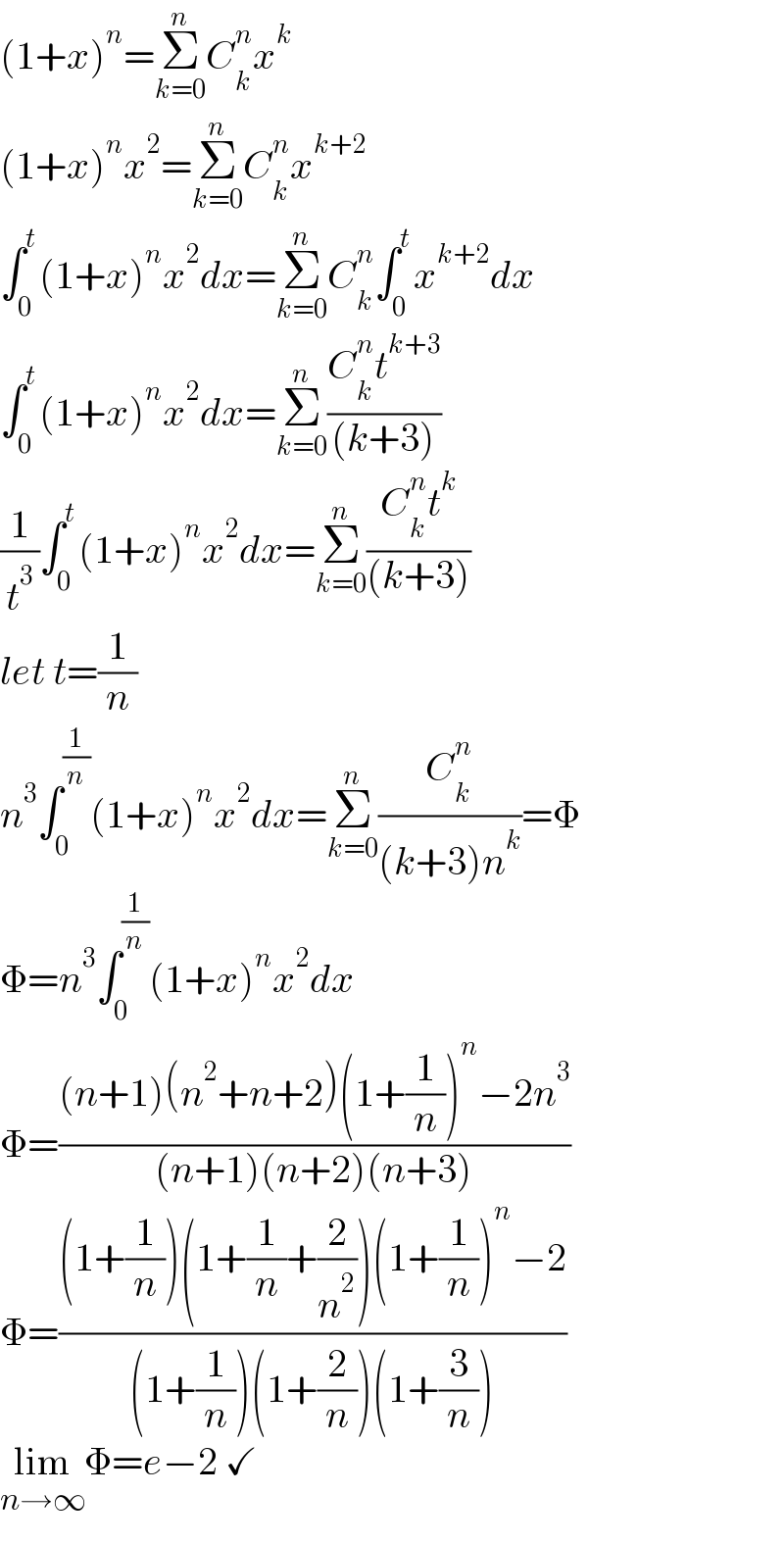
Commented by infinityaction last updated on 16/Sep/22

Commented by Tawa11 last updated on 18/Sep/22

| ||
Question and Answers Forum | ||
Question Number 176199 by infinityaction last updated on 14/Sep/22 | ||
 | ||
Answered by mr W last updated on 15/Sep/22 | ||
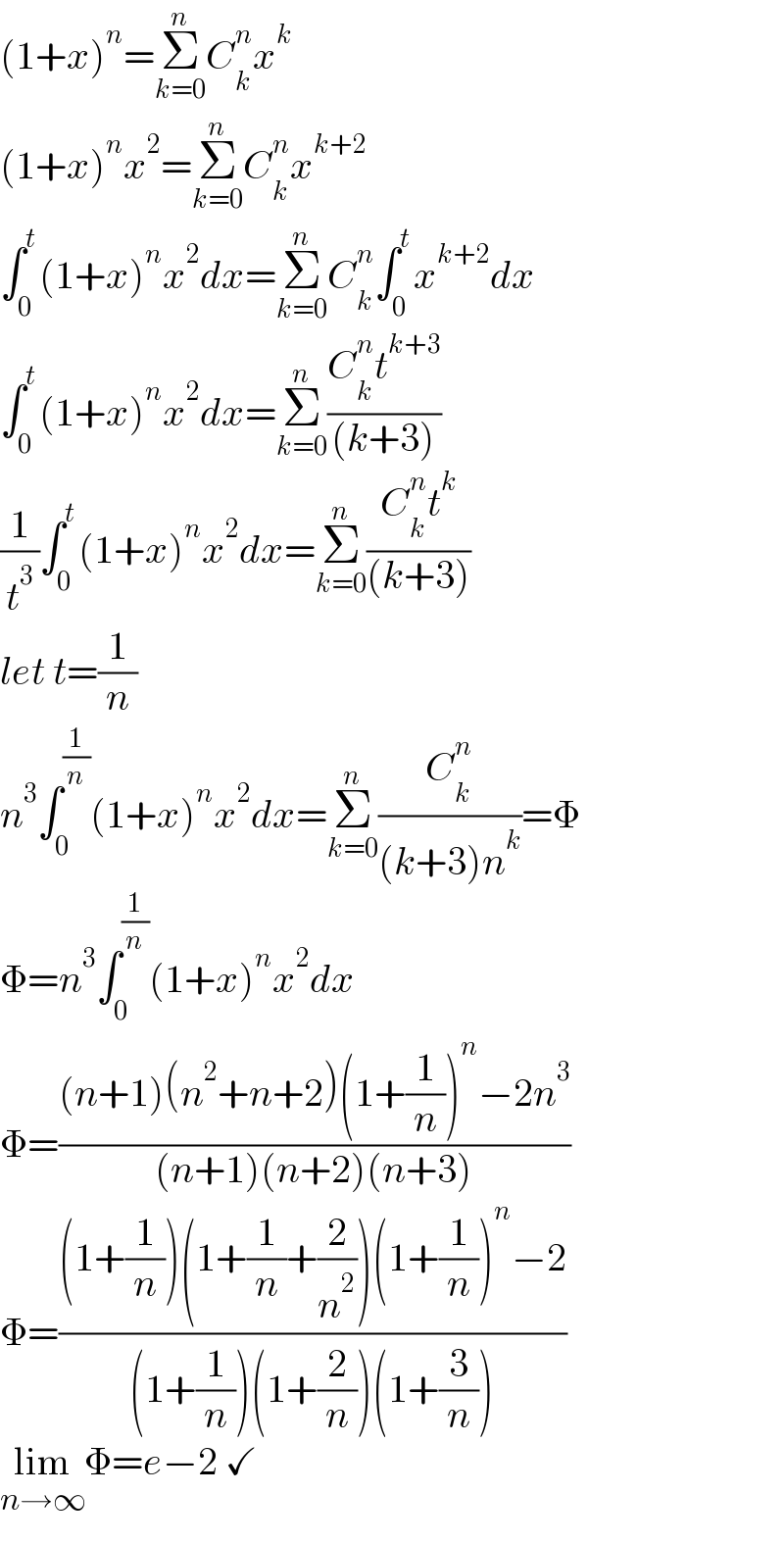 | ||
| ||
Commented by infinityaction last updated on 16/Sep/22 | ||
 | ||
Commented by Tawa11 last updated on 18/Sep/22 | ||
 | ||