Math Question and Answers


Question and Answers Forum

All Questions Topic List
Geometry Questions
Previous in All Question Next in All Question
Previous in Geometry Next in Geometry
Question Number 176367 by mr W last updated on 17/Sep/22

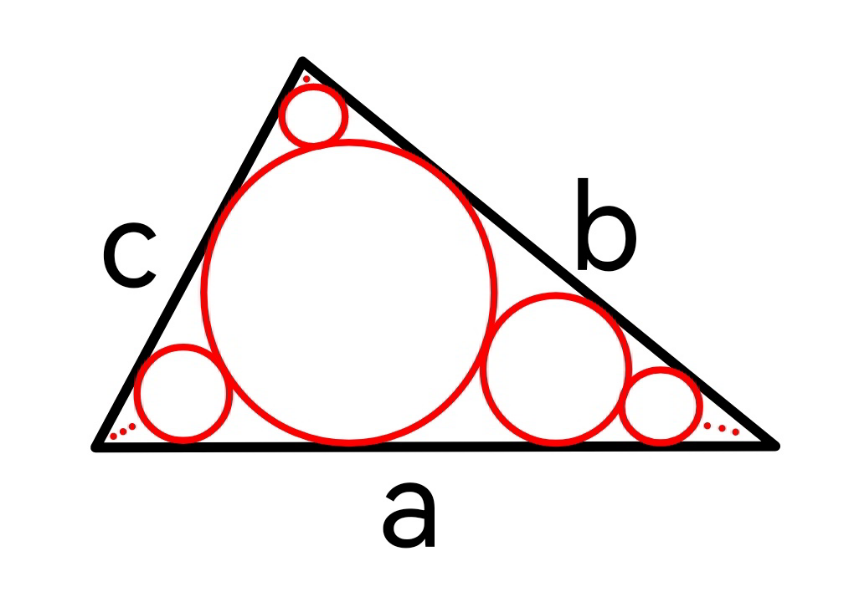
Commented by mr W last updated on 17/Sep/22

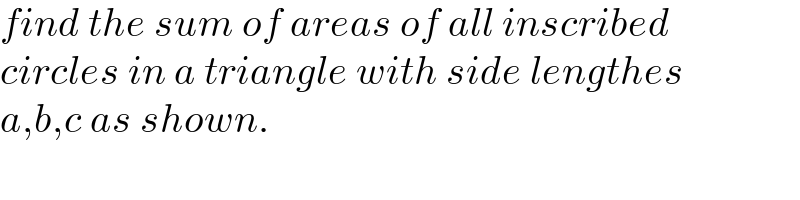
$f i n d t h e s u m o f a r e a s o f a l l i n s c r i b e d$ $c i r c l e s i n a t r i a n g l e w i t h s i d e l e n g t h e s$ $a, b, c a s s h o w n .$
	Answered by mr W last updated on 18/Sep/22

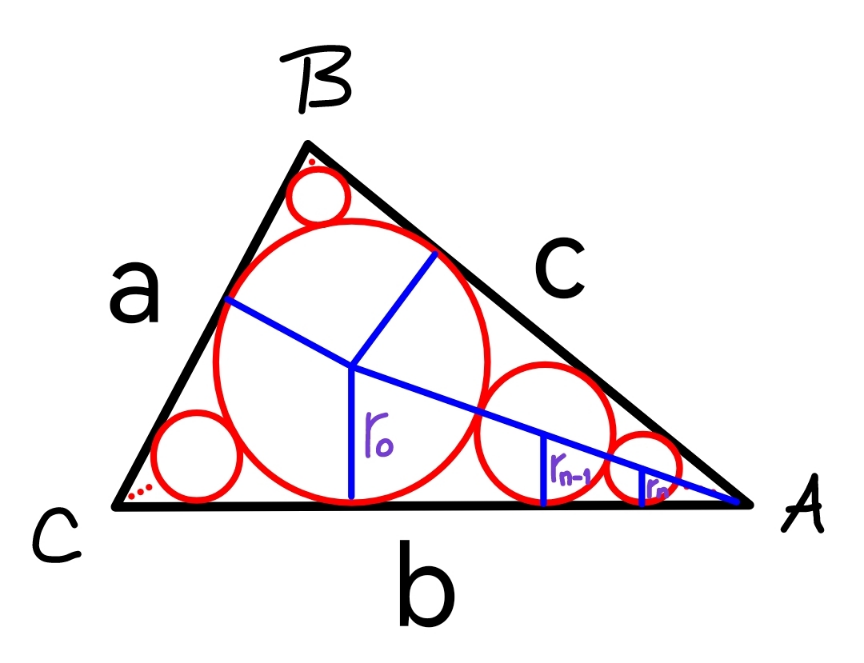
	Commented by mr W last updated on 19/Sep/22

	$l e t Δ = a r e a o f t h e t r i a n g l e$ $R = r a d i u s o f c i r c u m c i r c l e$ $r_{0} = r a d i u s o f i n c i r c l e$ $Δ = \frac{b c \sin A}{2} = \frac{a b c \sin A}{2 a} = \frac{a b c}{4 R}$ $r_{0} = \frac{2 Δ}{a + b + c}$ $\frac{r_{0}^{2}}{Δ} = \frac{4 Δ}{{(a + b + c)}^{2}} = \frac{a b c}{R {(a + b + c)}^{2}}$ $\frac{r_{0}^{2}}{Δ} = \frac{2 \sin A \sin B \sin C}{{(\sin A + \sin B + \sin C)}^{2}} = \tan \frac{A}{2} \tan \frac{B}{2} \tan \frac{C}{2}$ $\frac{r_{n - 1} - r_{n}}{r_{n - 1} + r_{n}} = \sin \frac{A}{2}$ $\frac{r_{n}}{r_{n - 1}} = \frac{1 - \sin \frac{A}{2}}{1 + \sin \frac{A}{2}}$ $\frac{r_{n}^{2}}{r_{n - 1}^{2}} = {(\frac{1 - \sin \frac{A}{2}}{1 + \sin \frac{A}{2}})}^{2} = q_{A} < 1 \Rightarrow G . P .$ $1 - q_{A} = (1 + \frac{1 - \sin \frac{A}{2}}{1 + \sin \frac{A}{2}}) (1 - \frac{1 - \sin \frac{A}{2}}{1 + \sin \frac{A}{2}})$ $1 - q_{A} = \frac{4 \sin \frac{A}{2}}{{(1 + \sin \frac{A}{2})}^{2}}$ $\frac{1}{1 - q_{A}} = \frac{{(1 + \sin \frac{A}{2})}^{2}}{4 \sin \frac{A}{2}} = \frac{1}{4} (\sin \frac{A}{2} + \frac{1}{\sin \frac{A}{2}}) + \frac{1}{2}$ $A_{n} = π r_{n}^{2}$ $\underset{n = 0}{\sum^{\infty}} A_{n} = π \underset{n = 0}{\sum^{\infty}} r_{n}^{2} = \frac{π r_{0}^{2}}{1 - q_{a}}$ $s u m o f a r e a s o f a l l i n s c r i b e d c i r c l e s :$ $A_{i . c .} = \frac{π r_{0}^{2}}{1 - q_{A}} + \frac{π r_{0}^{2}}{1 - q_{B}} + \frac{π r_{0}^{2}}{1 - q_{C}} - 2 π r_{0}^{2}$ $A_{i . c .} = (\frac{1}{1 - q_{A}} + \frac{1}{1 - q_{B}} + \frac{1}{1 - q_{C}} - 2) π r_{0}^{2}$ $A_{i . c .} = [\frac{1}{4} (\sin \frac{A}{2} + \sin \frac{B}{2} + \sin \frac{C}{2} + \frac{1}{\sin \frac{A}{2}} + \frac{1}{\sin \frac{B}{2}} + \frac{1}{\sin \frac{C}{2}}) + \frac{3}{2} - 2] π r_{0}^{2}$ $A_{i . c .} = (\sin \frac{A}{2} + \sin \frac{B}{2} + \sin \frac{C}{2} + \frac{1}{\sin \frac{A}{2}} + \frac{1}{\sin \frac{B}{2}} + \frac{1}{\sin \frac{C}{2}} - 2) \frac{π r_{0}^{2}}{4}$ $\frac{A_{i . c .}}{Δ} = (\sin \frac{A}{2} + \sin \frac{B}{2} + \sin \frac{C}{2} + \frac{1}{\sin \frac{A}{2}} + \frac{1}{\sin \frac{B}{2}} + \frac{1}{\sin \frac{C}{2}} - 2) \frac{π r_{0}^{2}}{4 Δ}$ $\frac{A_{i . c .}}{Δ} = \frac{π}{4} \tan \frac{A}{2} \tan \frac{B}{2} \tan \frac{C}{2} (\sin \frac{A}{2} + \sin \frac{B}{2} + \sin \frac{C}{2} + \frac{1}{\sin \frac{A}{2}} + \frac{1}{\sin \frac{B}{2}} + \frac{1}{\sin \frac{C}{2}} - 2)$ $e x a m p l e s :$ $A = 40 °, B = 60 °, C = 80 ° : \frac{A_{i . c .}}{Δ} \approx 0.826$ $A = 30 °, B = 40 °, C = 110 ° : \frac{A_{i . c .}}{Δ} \approx 0.812$ $A = 60 °, B = 60 °, C = 60 ° : \frac{A_{i . c .}}{Δ} = \frac{11 \sqrt{3} π}{72} \approx 0.831$
	Commented by Tawa11 last updated on 18/Sep/22

	$Wow, great sir .$
	Commented by behi834171 last updated on 18/Sep/22

	$s u p e r b!$ $f a n t a s t i c!$ $k u d o s t o y o u p r o p : m r W!$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum