
Question and Answers Forum
Question Number 176375 by cortano1 last updated on 17/Sep/22
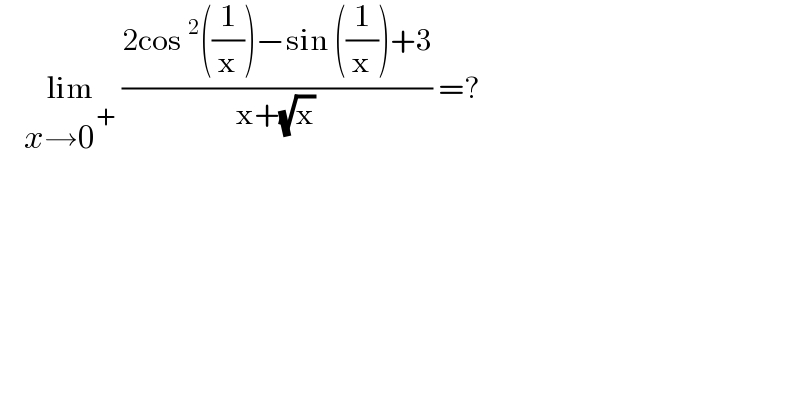
Commented by a.lgnaoui last updated on 18/Sep/22
 ((5(√X))/( (√X) +1))−(√X)sin X(((sin X +1)/( (√X) +1))) siut t=(√X) ((5t)/(t+1))−tsin (t^2 )(((sin (t^2 )+1)/(t+1))) ((5t)/(t+1))−(t/(t+1))[sin (t^2 )(sin (t^2 )+1] x→0+ t→+[∞ lim_(x→0+) =lim_(t→+∞) ((5t)/(t+1))−(t/(t+1))[sin (t^2 )(sin (t^2 )+1] =5−lim_(X→+∞) [sin(X)(sin (X)+1)] X=(2k+1)(π/2) sin X →1 donc lim_(x→0+) ((2cos^2 ((1/x))−sin ((1/x)))/(x+(√x)))=5−2=3](Q176431.png)
Commented by peter frank last updated on 19/Sep/22
| ||
Question and Answers Forum | ||
Question Number 176375 by cortano1 last updated on 17/Sep/22 | ||
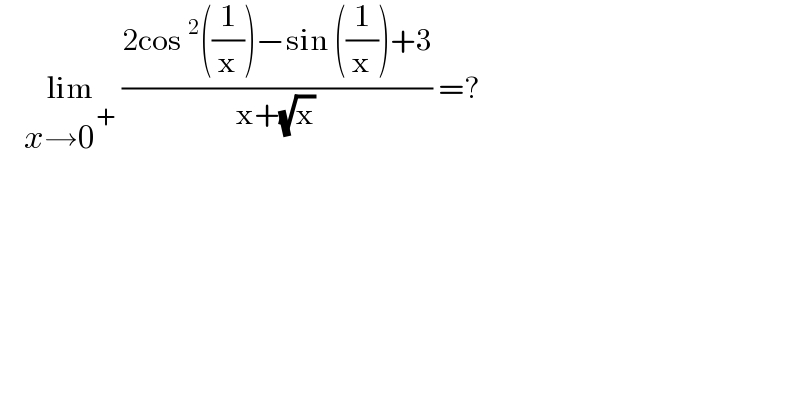 | ||
Commented by a.lgnaoui last updated on 18/Sep/22 | ||
 ((5(√X))/( (√X) +1))−(√X)sin X(((sin X +1)/( (√X) +1))) siut t=(√X) ((5t)/(t+1))−tsin (t^2 )(((sin (t^2 )+1)/(t+1))) ((5t)/(t+1))−(t/(t+1))[sin (t^2 )(sin (t^2 )+1] x→0+ t→+[∞ lim_(x→0+) =lim_(t→+∞) ((5t)/(t+1))−(t/(t+1))[sin (t^2 )(sin (t^2 )+1] =5−lim_(X→+∞) [sin(X)(sin (X)+1)] X=(2k+1)(π/2) sin X →1 donc lim_(x→0+) ((2cos^2 ((1/x))−sin ((1/x)))/(x+(√x)))=5−2=3](Q176431.png) | ||
Commented by peter frank last updated on 19/Sep/22 | ||
 | ||