Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 176387 by cortano1 last updated on 19/Sep/22

x^3 +(1/x^3 ) = 1 ⇒(([x^5 +(1/x^5 )]^3 −1)/(x^5 +(1/x^5 ))) =?

$$\:\:\mathrm{x}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\:=\:\mathrm{1}\:\Rightarrow\frac{\left[\mathrm{x}^{\mathrm{5}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{5}} }\right]^{\mathrm{3}} −\mathrm{1}}{\mathrm{x}^{\mathrm{5}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{5}} }}\:=? \\ $$

Commented by mr W last updated on 18/Sep/22

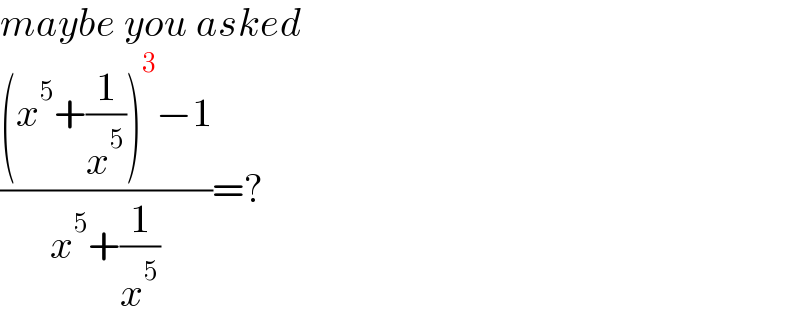
maybe you asked (((x^5 +(1/x^5 ))^3 −1)/(x^5 +(1/x^5 )))=?

$${maybe}\:{you}\:{asked} \\ $$$$\frac{\left({x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }\right)^{\mathrm{3}} −\mathrm{1}}{{x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }}=? \\ $$

Commented by cortano1 last updated on 19/Sep/22

oo yes. typo

$$\mathrm{oo}\:\mathrm{yes}.\:\mathrm{typo} \\ $$

Commented by mr W last updated on 19/Sep/22

(((x^5 +(1/x^5 ))^3 −1)/(x^5 +(1/x^5 )))=3

$$\frac{\left({x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }\right)^{\mathrm{3}} −\mathrm{1}}{{x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }}=\mathrm{3} \\ $$

Commented by cortano1 last updated on 19/Sep/22

nice

$$\mathrm{nice} \\ $$

Commented by cortano1 last updated on 19/Sep/22

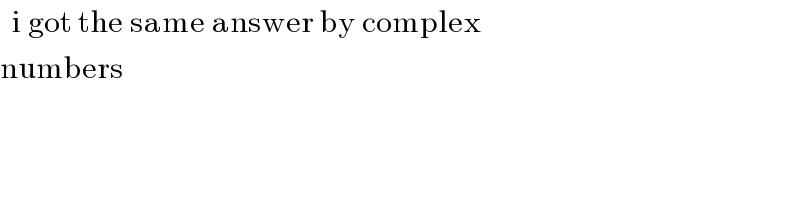
i got the same answer by complex numbers

$$\:\:\mathrm{i}\:\mathrm{got}\:\mathrm{the}\:\mathrm{same}\:\mathrm{answer}\:\mathrm{by}\:\mathrm{complex} \\ $$$$\mathrm{numbers} \\ $$

Answered by BaliramKumar last updated on 18/Sep/22

((2sin(10°)+1)/(2sin(10°)))

$$\frac{\mathrm{2}{sin}\left(\mathrm{10}°\right)+\mathrm{1}}{\mathrm{2}{sin}\left(\mathrm{10}°\right)} \\ $$

Answered by Rasheed.Sindhi last updated on 19/Sep/22

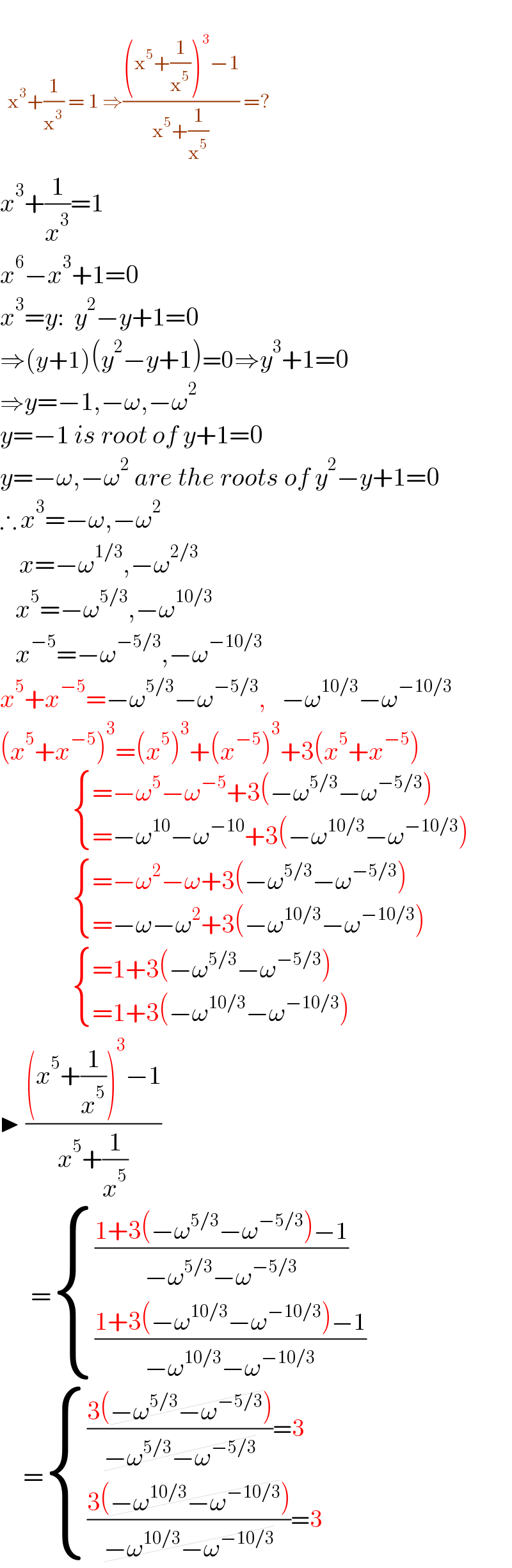
x^3 +(1/x^3 ) = 1 ⇒(((x^5 +(1/x^5 ))^3 −1)/(x^5 +(1/x^5 ))) =? x^3 +(1/x^3 )=1 x^6 −x^3 +1=0 x^3 =y: y^2 −y+1=0 ⇒(y+1)(y^2 −y+1)=0⇒y^3 +1=0 ⇒y=−1,−ω,−ω^2 y=−1 is root of y+1=0 y=−ω,−ω^2 are the roots of y^2 −y+1=0 ∴ x^3 =−ω,−ω^2 x=−ω^(1/3) ,−ω^(2/3) x^5 =−ω^(5/3) ,−ω^(10/3) x^(−5) =−ω^(−5/3) ,−ω^(−10/3) x^5 +x^(−5) =−ω^(5/3) −ω^(−5/3) , −ω^(10/3) −ω^(−10/3) (x^5 +x^(−5) )^3 =(x^5 )^3 +(x^(−5) )^3 +3(x^5 +x^(−5) ) { ((=−ω^5 −ω^(−5) +3(−ω^(5/3) −ω^(−5/3) ) )),((=−ω^(10) −ω^(−10) +3(−ω^(10/3) −ω^(−10/3) ))) :} { ((=−ω^2 −ω+3(−ω^(5/3) −ω^(−5/3) ) )),((=−ω−ω^2 +3(−ω^(10/3) −ω^(−10/3) ))) :} { ((=1+3(−ω^(5/3) −ω^(−5/3) ) )),((=1+3(−ω^(10/3) −ω^(−10/3) ))) :} ▶ (((x^5 +(1/x^5 ))^3 −1)/(x^5 +(1/x^5 ))) = { (((1+3(−ω^(5/3) −ω^(−5/3) )−1)/(−ω^(5/3) −ω^(−5/3) ))),(((1+3(−ω^(10/3) −ω^(−10/3) )−1)/(−ω^(10/3) −ω^(−10/3) ))) :} = { ((((3(−ω^(5/3) −ω^(−5/3) ))/(−ω^(5/3) −ω^(−5/3) ))=3)),((((3(−ω^(10/3) −ω^(−10/3) ))/(−ω^(10/3) −ω^(−10/3) ))=3)) :}

$$ \\ $$$$\:\:\mathrm{x}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\:=\:\mathrm{1}\:\Rightarrow\frac{\left(\mathrm{x}^{\mathrm{5}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{5}} }\right)^{\mathrm{3}} −\mathrm{1}}{\mathrm{x}^{\mathrm{5}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{5}} }}\:=? \\ $$$${x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }=\mathrm{1} \\ $$$${x}^{\mathrm{6}} −{x}^{\mathrm{3}} +\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{3}} ={y}:\:\:{y}^{\mathrm{2}} −{y}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left({y}+\mathrm{1}\right)\left({y}^{\mathrm{2}} −{y}+\mathrm{1}\right)=\mathrm{0}\Rightarrow{y}^{\mathrm{3}} +\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{y}=−\mathrm{1},−\omega,−\omega^{\mathrm{2}} \\ $$$${y}=−\mathrm{1}\:{is}\:{root}\:{of}\:{y}+\mathrm{1}=\mathrm{0} \\ $$$${y}=−\omega,−\omega^{\mathrm{2}} \:{are}\:{the}\:{roots}\:{of}\:{y}^{\mathrm{2}} −{y}+\mathrm{1}=\mathrm{0} \\ $$$$\therefore\:{x}^{\mathrm{3}} =−\omega,−\omega^{\mathrm{2}} \\ $$$$\:\:\:\:\:{x}=−\omega^{\mathrm{1}/\mathrm{3}} ,−\omega^{\mathrm{2}/\mathrm{3}} \\ $$$$\:\:\:\:{x}^{\mathrm{5}} =−\omega^{\mathrm{5}/\mathrm{3}} ,−\omega^{\mathrm{10}/\mathrm{3}} \\ $$$$\:\:\:\:{x}^{−\mathrm{5}} =−\omega^{−\mathrm{5}/\mathrm{3}} ,−\omega^{−\mathrm{10}/\mathrm{3}} \\ $$$${x}^{\mathrm{5}} +{x}^{−\mathrm{5}} =−\omega^{\mathrm{5}/\mathrm{3}} −\omega^{−\mathrm{5}/\mathrm{3}} ,\:\:\:−\omega^{\mathrm{10}/\mathrm{3}} −\omega^{−\mathrm{10}/\mathrm{3}} \\ $$$$\left({x}^{\mathrm{5}} +{x}^{−\mathrm{5}} \right)^{\mathrm{3}} =\left({x}^{\mathrm{5}} \right)^{\mathrm{3}} +\left({x}^{−\mathrm{5}} \right)^{\mathrm{3}} +\mathrm{3}\left({x}^{\mathrm{5}} +{x}^{−\mathrm{5}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\begin{cases}{=−\omega^{\mathrm{5}} −\omega^{−\mathrm{5}} +\mathrm{3}\left(−\omega^{\mathrm{5}/\mathrm{3}} −\omega^{−\mathrm{5}/\mathrm{3}} \right)\:}\\{=−\omega^{\mathrm{10}} −\omega^{−\mathrm{10}} +\mathrm{3}\left(−\omega^{\mathrm{10}/\mathrm{3}} −\omega^{−\mathrm{10}/\mathrm{3}} \right)}\end{cases}\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\begin{cases}{=−\omega^{\mathrm{2}} −\omega+\mathrm{3}\left(−\omega^{\mathrm{5}/\mathrm{3}} −\omega^{−\mathrm{5}/\mathrm{3}} \right)\:}\\{=−\omega−\omega^{\mathrm{2}} +\mathrm{3}\left(−\omega^{\mathrm{10}/\mathrm{3}} −\omega^{−\mathrm{10}/\mathrm{3}} \right)}\end{cases}\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\begin{cases}{=\mathrm{1}+\mathrm{3}\left(−\omega^{\mathrm{5}/\mathrm{3}} −\omega^{−\mathrm{5}/\mathrm{3}} \right)\:}\\{=\mathrm{1}+\mathrm{3}\left(−\omega^{\mathrm{10}/\mathrm{3}} −\omega^{−\mathrm{10}/\mathrm{3}} \right)}\end{cases}\:\: \\ $$$$\blacktriangleright\:\frac{\left({x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }\right)^{\mathrm{3}} −\mathrm{1}}{{x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }} \\ $$$$\:\:\:\:\:\:=\begin{cases}{\frac{\mathrm{1}+\mathrm{3}\left(−\omega^{\mathrm{5}/\mathrm{3}} −\omega^{−\mathrm{5}/\mathrm{3}} \right)−\mathrm{1}}{−\omega^{\mathrm{5}/\mathrm{3}} −\omega^{−\mathrm{5}/\mathrm{3}} }}\\{\frac{\mathrm{1}+\mathrm{3}\left(−\omega^{\mathrm{10}/\mathrm{3}} −\omega^{−\mathrm{10}/\mathrm{3}} \right)−\mathrm{1}}{−\omega^{\mathrm{10}/\mathrm{3}} −\omega^{−\mathrm{10}/\mathrm{3}} }}\end{cases}\: \\ $$$$\:\:\:\:\:\:=\begin{cases}{\frac{\mathrm{3}\left(\cancel{−\omega^{\mathrm{5}/\mathrm{3}} −\omega^{−\mathrm{5}/\mathrm{3}} }\right)}{\cancel{−\omega^{\mathrm{5}/\mathrm{3}} −\omega^{−\mathrm{5}/\mathrm{3}} }}=\mathrm{3}}\\{\frac{\mathrm{3}\left(\cancel{−\omega^{\mathrm{10}/\mathrm{3}} −\omega^{−\mathrm{10}/\mathrm{3}} }\right)}{\cancel{−\omega^{\mathrm{10}/\mathrm{3}} −\omega^{−\mathrm{10}/\mathrm{3}} }}=\mathrm{3}}\end{cases}\: \\ $$

Commented by mr W last updated on 19/Sep/22

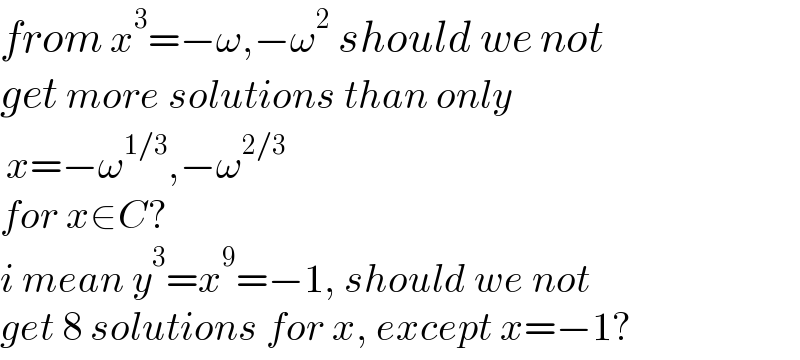
from x^3 =−ω,−ω^2 should we not get more solutions than only x=−ω^(1/3) ,−ω^(2/3) for x∈C? i mean y^3 =x^9 =−1, should we not get 8 solutions for x, except x=−1?

$${from}\:{x}^{\mathrm{3}} =−\omega,−\omega^{\mathrm{2}} \:{should}\:{we}\:{not} \\ $$$${get}\:{more}\:{solutions}\:{than}\:{only} \\ $$$$\:{x}=−\omega^{\mathrm{1}/\mathrm{3}} ,−\omega^{\mathrm{2}/\mathrm{3}} \\ $$$${for}\:{x}\in{C}? \\ $$$${i}\:{mean}\:{y}^{\mathrm{3}} ={x}^{\mathrm{9}} =−\mathrm{1},\:{should}\:{we}\:{not} \\ $$$${get}\:\mathrm{8}\:{solutions}\:{for}\:{x},\:{except}\:{x}=−\mathrm{1}? \\ $$

Commented by Rasheed.Sindhi last updated on 19/Sep/22

You′re right as always sir! x^3 =−ω,−ω^2 have ofcourse more solurions! But then this approach will be too complicated and we have to look for another approach!

$${You}'{re}\:{right}\:{as}\:{always}\:\boldsymbol{{sir}}! \\ $$$${x}^{\mathrm{3}} =−\omega,−\omega^{\mathrm{2}} \:{have}\:{ofcourse}\:{more} \\ $$$$\:{solurions}!\:\mathcal{B}{ut}\:{then}\:{this}\:{approach} \\ $$$${will}\:{be}\:{too}\:{complicated}\:{and}\:{we} \\ $$$${have}\:{to}\:{look}\:{for}\:{another}\:{approach}! \\ $$

Commented by mr W last updated on 19/Sep/22

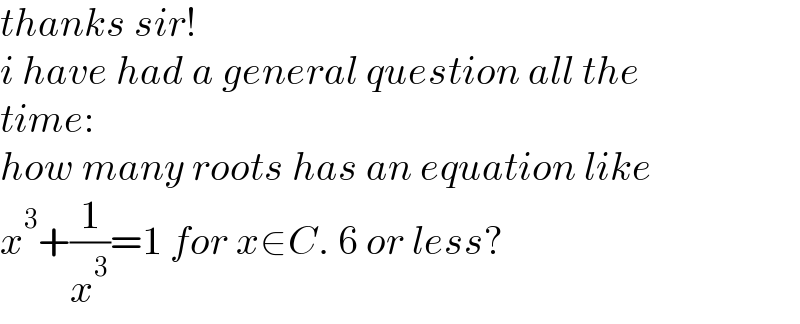
thanks sir! i have had a general question all the time: how many roots has an equation like x^3 +(1/x^3 )=1 for x∈C. 6 or less?

$${thanks}\:{sir}! \\ $$$${i}\:{have}\:{had}\:{a}\:{general}\:{question}\:{all}\:{the} \\ $$$${time}: \\ $$$${how}\:{many}\:{roots}\:{has}\:{an}\:{equation}\:{like} \\ $$$${x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }=\mathrm{1}\:{for}\:{x}\in{C}.\:\mathrm{6}\:{or}\:{less}? \\ $$

Commented by cortano1 last updated on 19/Sep/22

thanks you

$$\mathrm{thanks}\:\mathrm{you} \\ $$

Answered by mr W last updated on 18/Sep/22

x+(1/x)=a, say x^2 +(1/x^2 )=a^2 −2 (x^2 +(1/x^2 ))(x+(1/x))=(a^2 −2)a x^3 +(1/x^3 )+x+(1/x)=(a^2 −2)a 1+a=(a^2 −2)a a^3 −3a−1=0 ⇒a=2 sin (((2kπ)/3)−(π/(18))) (k=0,1,2) (x^3 +(1/x^3 ))(x^2 +(1/x^2 ))=1×(a^2 −2) x^5 +(1/x^5 )+x+(1/x)=1×(a^2 −2) x^5 +(1/x^5 )+a=a^2 −2 ⇒x^5 +(1/x^5 )=a^2 −a−2=(a+1)(a−2) ((x^5 +(1/x^5 )−1)/(x^5 +(1/x^5 )))=1−(1/((a+1)(a−2))) =1−(1/(4[sin (((2kπ)/3)−(π/(18)))+(1/2)][sin (((2kπ)/3)−(π/(18)))−1]))

$${x}+\frac{\mathrm{1}}{{x}}={a},\:{say} \\ $$$${x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }={a}^{\mathrm{2}} −\mathrm{2} \\ $$$$\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\left({x}+\frac{\mathrm{1}}{{x}}\right)=\left({a}^{\mathrm{2}} −\mathrm{2}\right){a} \\ $$$${x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }+{x}+\frac{\mathrm{1}}{{x}}=\left({a}^{\mathrm{2}} −\mathrm{2}\right){a} \\ $$$$\mathrm{1}+{a}=\left({a}^{\mathrm{2}} −\mathrm{2}\right){a} \\ $$$${a}^{\mathrm{3}} −\mathrm{3}{a}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{a}=\mathrm{2}\:\mathrm{sin}\:\left(\frac{\mathrm{2}{k}\pi}{\mathrm{3}}−\frac{\pi}{\mathrm{18}}\right)\:\left({k}=\mathrm{0},\mathrm{1},\mathrm{2}\right) \\ $$$$ \\ $$$$\left({x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)=\mathrm{1}×\left({a}^{\mathrm{2}} −\mathrm{2}\right) \\ $$$${x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }+{x}+\frac{\mathrm{1}}{{x}}=\mathrm{1}×\left({a}^{\mathrm{2}} −\mathrm{2}\right) \\ $$$${x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }+{a}={a}^{\mathrm{2}} −\mathrm{2} \\ $$$$\Rightarrow{x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }={a}^{\mathrm{2}} −{a}−\mathrm{2}=\left({a}+\mathrm{1}\right)\left({a}−\mathrm{2}\right) \\ $$$$\frac{{x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }−\mathrm{1}}{{x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }}=\mathrm{1}−\frac{\mathrm{1}}{\left({a}+\mathrm{1}\right)\left({a}−\mathrm{2}\right)} \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}\left[\mathrm{sin}\:\left(\frac{\mathrm{2}{k}\pi}{\mathrm{3}}−\frac{\pi}{\mathrm{18}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\right]\left[\mathrm{sin}\:\left(\frac{\mathrm{2}{k}\pi}{\mathrm{3}}−\frac{\pi}{\mathrm{18}}\right)−\mathrm{1}\right]} \\ $$

Commented by Tawa11 last updated on 19/Sep/22

Great sirs

$$\mathrm{Great}\:\mathrm{sirs} \\ $$

Answered by Rasheed.Sindhi last updated on 19/Sep/22

x^3 +(1/x^3 ) = 1 ⇒(([x^5 +(1/x^5 )]^3 −1)/(x^5 +(1/x^5 ))) =? x^6 −x^3 +1=0 x^6 =x^3 −1 { ((x^(12) =x^6 −2x^3 +1=x^3 −1−2x^3 +1=−x^3 )),((x^(−12) =(1/x^(12) )=(1/(−x^3 ))=−(1/x^3 ))) :} { ((x^(15) =x^(12) ∙x^3 =−x^3 ∙x^3 =−x^6 )),((x^(−15) =(1/x^(15) )=−(1/x^6 ))) :} .... x^(15) =x^(12) ∙x^3 =−x^6 =−(x^3 −1)=1−x^3 x^3 =1−x^(−3) x^5 =x^3 ∙x^2 =x^2 −x^(−1) x^(−3) =1−x^3 x^(−5) =x^(−3) ∙x^(−2) =x^(−2) −x x^5 +(1/x^5 )=x^2 −x^(−1) +x^(−2) −x =x^2 +(1/x^2 )−(x+(1/x)) Continue...

$$\:\:\mathrm{x}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\:=\:\mathrm{1}\:\Rightarrow\frac{\left[\mathrm{x}^{\mathrm{5}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{5}} }\right]^{\mathrm{3}} −\mathrm{1}}{\mathrm{x}^{\mathrm{5}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{5}} }}\:=? \\ $$$${x}^{\mathrm{6}} −{x}^{\mathrm{3}} +\mathrm{1}=\mathrm{0} \\ $$$${x}^{\mathrm{6}} ={x}^{\mathrm{3}} −\mathrm{1} \\ $$$$\begin{cases}{{x}^{\mathrm{12}} ={x}^{\mathrm{6}} −\mathrm{2}{x}^{\mathrm{3}} +\mathrm{1}={x}^{\mathrm{3}} −\mathrm{1}−\mathrm{2}{x}^{\mathrm{3}} +\mathrm{1}=−{x}^{\mathrm{3}} }\\{{x}^{−\mathrm{12}} =\frac{\mathrm{1}}{{x}^{\mathrm{12}} }=\frac{\mathrm{1}}{−{x}^{\mathrm{3}} }=−\frac{\mathrm{1}}{{x}^{\mathrm{3}} }}\end{cases}\: \\ $$$$\begin{cases}{{x}^{\mathrm{15}} ={x}^{\mathrm{12}} \centerdot{x}^{\mathrm{3}} =−{x}^{\mathrm{3}} \centerdot{x}^{\mathrm{3}} =−{x}^{\mathrm{6}} }\\{{x}^{−\mathrm{15}} =\frac{\mathrm{1}}{{x}^{\mathrm{15}} }=−\frac{\mathrm{1}}{{x}^{\mathrm{6}} }}\end{cases}\: \\ $$$$.... \\ $$$${x}^{\mathrm{15}} ={x}^{\mathrm{12}} \centerdot{x}^{\mathrm{3}} =−{x}^{\mathrm{6}} =−\left({x}^{\mathrm{3}} −\mathrm{1}\right)=\mathrm{1}−{x}^{\mathrm{3}} \\ $$$${x}^{\mathrm{3}} =\mathrm{1}−{x}^{−\mathrm{3}} \\ $$$${x}^{\mathrm{5}} ={x}^{\mathrm{3}} \centerdot{x}^{\mathrm{2}} ={x}^{\mathrm{2}} −{x}^{−\mathrm{1}} \\ $$$${x}^{−\mathrm{3}} =\mathrm{1}−{x}^{\mathrm{3}} \\ $$$${x}^{−\mathrm{5}} ={x}^{−\mathrm{3}} \centerdot{x}^{−\mathrm{2}} ={x}^{−\mathrm{2}} −{x} \\ $$$${x}^{\mathrm{5}} +\frac{\mathrm{1}}{{x}^{\mathrm{5}} }={x}^{\mathrm{2}} −{x}^{−\mathrm{1}} +{x}^{−\mathrm{2}} −{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\left({x}+\frac{\mathrm{1}}{{x}}\right) \\ $$$${Continue}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com