
Question and Answers Forum
Question Number 176490 by mnjuly1970 last updated on 20/Sep/22
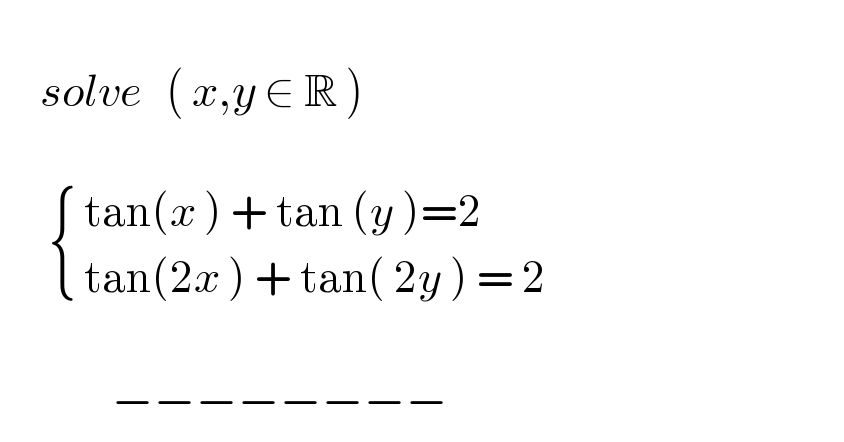
Answered by ajfour last updated on 20/Sep/22
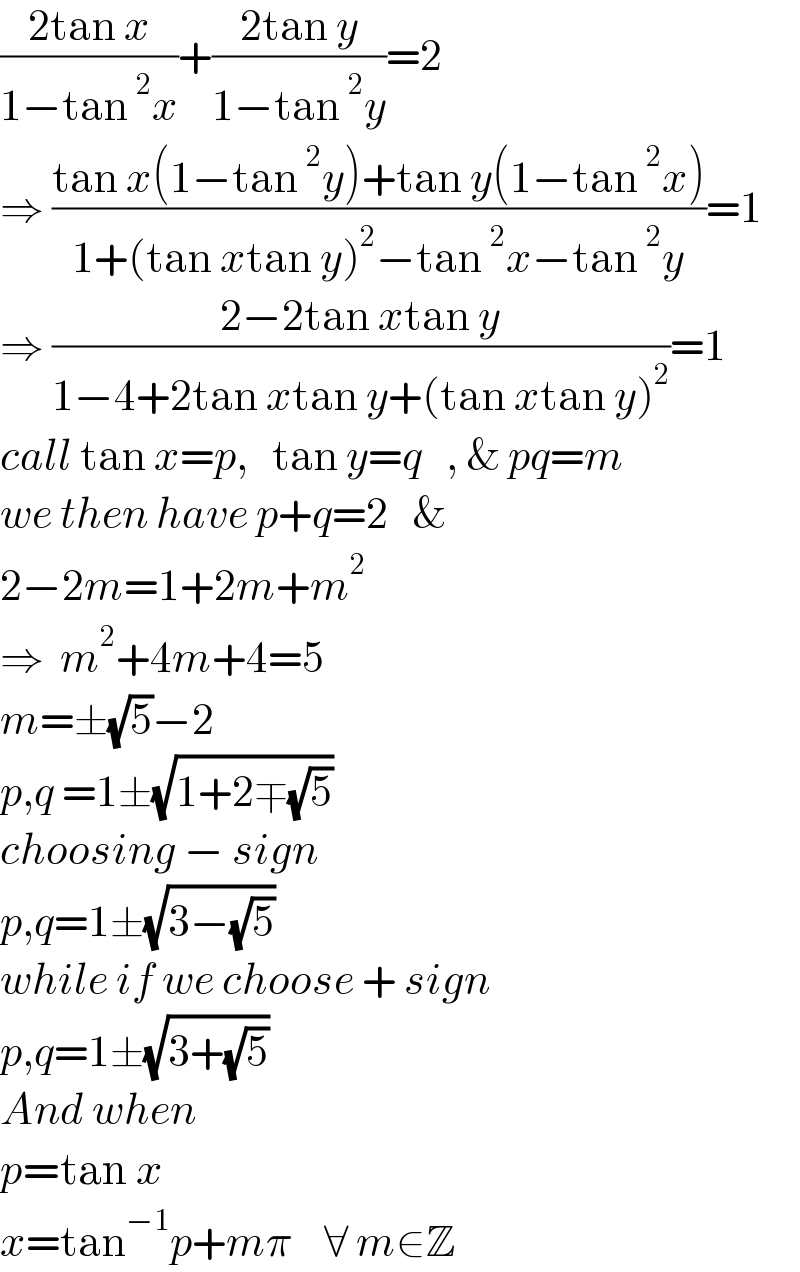
Commented by Tawa11 last updated on 20/Sep/22

Commented by Tawa11 last updated on 20/Sep/22

Commented by ajfour last updated on 20/Sep/22
https://youtu.be/GmIVICE0YrQ
Commented by mnjuly1970 last updated on 20/Sep/22
Commented by ajfour last updated on 20/Sep/22
Answered by behi834171 last updated on 20/Sep/22
![tgx=m,tgy=n tg(x+y)=(2/(1−mn)) tg(2x+2y)=(2/(1−((2m)/(1−m^2 )).((2n)/(1−n^2 )))) tg(2x+2y)=((2×(2/(1−mn)))/(1−(4/((1−mn)^2 ))))=((4(1−mn))/((1−mn)^2 −4)) ⇒((1−m^2 −n^2 +m^2 n^2 )/(1−n^2 −m^2 +m^2 n^2 −4mn))=((2−2mn)/(m^2 n^2 −2mn−3))⇒ m^2 n^2 −2mn−3−m^4 n^2 +2m^3 n+3m^2 −m^2 n^4 +2mn^3 +3n^2 +m^4 n^4 −2m^3 n^3 −3m^2 n^2 = 2−2n^2 −2m^2 +2m^2 n^2 −8mn−2mn+ 4mn^3 +4m^3 n−2m^3 n^3 +8mn⇒ −2m^2 n^2 −2mn−3−m^4 n^2 +2m^3 n+3m^2 −m^2 n^4 +2mn^3 +3n^2 +m^4 n^4 −2m^3 n^3 −3m^2 n^2 = 2−2n^2 −2m^2 +2m^2 n^2 −2mn+4mn^3 + 4m^3 n−2m^3 n^3 ⇒ −4m^2 n^2 −5−m^4 n^2 −2m^3 n+5m^2 −m^2 n^4 −2mn^3 +5m^2 +m^4 n^4 =0⇒ m^4 n^4 −2m^3 n−2mn^3 −m^4 n^2 −m^2 n^4 −4m^2 n^2 +5m^2 +5n^2 −5=0 ⇒t^4 −3t(m^2 +n^2 )−t^2 (m^2 +n^2 )−4t^2 + +5(m^2 +n^2 )−5=0 ⇒t^4 −3t(4−2t)−t^2 (4−2t)−4t^2 + +5(4−2t)−5=0⇒ t^4 −12t+6t^2 −4t^2 +2t^3 −4t^2 +20−10t−5=0 ⇒t^4 +2t^3 −2t^2 −22t+15=0⇒ t=mn=0.67, t=mn=2.16 ⇒ { ((m+n=2)),((mn=0.67 or 2.16)) :} ⇒z^2 −2z+[0.67 or 2.16]=0 ⇒z−1=±0.57 ⇒ { ((tgx=1.57 or 0.43)),((tgy=0.43 or 1.57)) :}](Q176548.png)
Commented by Tawa11 last updated on 22/Sep/22

