
Question and Answers Forum
Question Number 176542 by mnjuly1970 last updated on 20/Sep/22
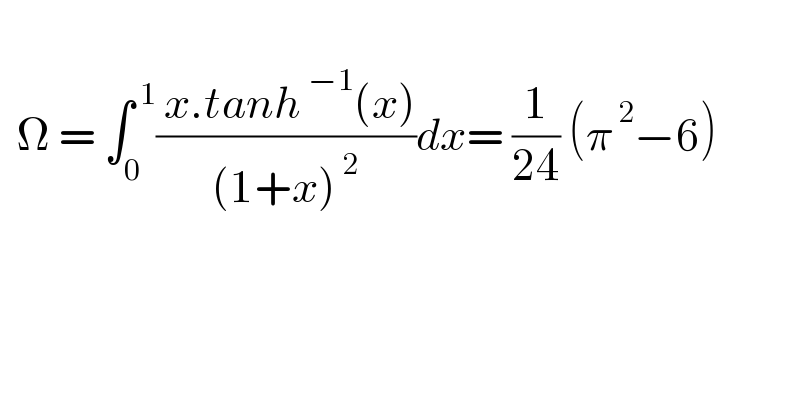
Answered by Peace last updated on 20/Sep/22
![∫_0 ^1 (x/((1+x)^2 ))tg^− (x)dx tanh^− (x)=(1/2)(ln(1+x)−ln(1−x)) (x/((1+x)^2 ))=(1/(1+x))−(1/((1+x)^2 )) 2Ω=∫_0 ^1 ((ln(1+x))/(1+x))−((ln(1+x))/((1+x)^2 ))dx+∫_0 ^1 ((ln(1−x))/((1+x)^2 ))dx−∫_0 ^1 ((ln(1−x))/(1+x))dx =(1/2)[ln^2 (1+x)]_0 ^1 +[((ln(1+x))/(1+x))]_0 ^1 −∫_0 ^1 (1/((1+x)^2 ))+A+B =((ln^2 (2))/2)+((ln(2))/2)+(1/2)+A+B A=lim_(x→1) ∫_0 ^x ((ln(1−t))/((1+t)^2 ))dt=lim_(x→1) {−((ln(1−x))/(1+x))−∫_0 ^x (1/(1−t^2 )).dt} =lim_(x→1) −((ln(1−x))/(1+x))−(1/2)∫_0 ^x (1/(1−t))+(1/(1+t))dt =lim_(x→1) −((ln(1−x))/(1+x))+((ln(1−x))/2)−((ln(1+x))/2) =−((ln(2))/2) −B=∫_0 ^1 ((ln(1−x))/(1+x))dx x=((1−t)/(1+t)),=−1+(2/(1+t))⇒dt=−((2dt)/((1+t)^2 )) 2∫_0 ^1 ((ln(((2t)/(1+t))))/(2/((1+t)))).(1/((1+t)^2 ))dt=∫_0 ^1 ((ln(2t)−ln(1+t))/(1+t))dt =∫_0 ^1 ((ln(2))/(1+t))+((ln(t))/(1+t))−((ln(1+t))/(1+t))dt =ln^2 (2)−((ln^2 (2))/2)+∫_0 ^1 ((ln(t))/(1+t))dt=((ln^2 (2))/2)+∫_0 ^1 ((ln(1−(−t))/(−t))d(−t) =((ln^2 (2))/2)−Li_2 (−1) B=−((ln^2 (2))/2)+Li_2 (−1) 2Ω=((ln^2 (2))/2)+((ln(2))/2)+(1/2)+A+B =((ln^2 (2))/2)+((ln(2))/2)+(1/2)−((ln(2))/2)−((ln^2 (2))/2)+Li_2 (−1) =(1/2)+Li_2 (−1)=(1/2)+(π^2 /(12))=(1/(12))(π^2 −6) Ω=(1/(24))(π^2 −6)](Q176545.png)
Commented by Tawa11 last updated on 22/Sep/22

Commented by Peace last updated on 23/Sep/22
| ||
Question and Answers Forum | ||
Question Number 176542 by mnjuly1970 last updated on 20/Sep/22 | ||
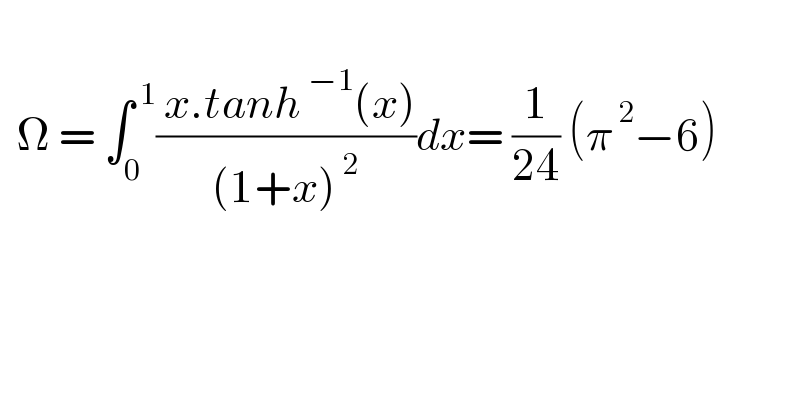 | ||
Answered by Peace last updated on 20/Sep/22 | ||
![∫_0 ^1 (x/((1+x)^2 ))tg^− (x)dx tanh^− (x)=(1/2)(ln(1+x)−ln(1−x)) (x/((1+x)^2 ))=(1/(1+x))−(1/((1+x)^2 )) 2Ω=∫_0 ^1 ((ln(1+x))/(1+x))−((ln(1+x))/((1+x)^2 ))dx+∫_0 ^1 ((ln(1−x))/((1+x)^2 ))dx−∫_0 ^1 ((ln(1−x))/(1+x))dx =(1/2)[ln^2 (1+x)]_0 ^1 +[((ln(1+x))/(1+x))]_0 ^1 −∫_0 ^1 (1/((1+x)^2 ))+A+B =((ln^2 (2))/2)+((ln(2))/2)+(1/2)+A+B A=lim_(x→1) ∫_0 ^x ((ln(1−t))/((1+t)^2 ))dt=lim_(x→1) {−((ln(1−x))/(1+x))−∫_0 ^x (1/(1−t^2 )).dt} =lim_(x→1) −((ln(1−x))/(1+x))−(1/2)∫_0 ^x (1/(1−t))+(1/(1+t))dt =lim_(x→1) −((ln(1−x))/(1+x))+((ln(1−x))/2)−((ln(1+x))/2) =−((ln(2))/2) −B=∫_0 ^1 ((ln(1−x))/(1+x))dx x=((1−t)/(1+t)),=−1+(2/(1+t))⇒dt=−((2dt)/((1+t)^2 )) 2∫_0 ^1 ((ln(((2t)/(1+t))))/(2/((1+t)))).(1/((1+t)^2 ))dt=∫_0 ^1 ((ln(2t)−ln(1+t))/(1+t))dt =∫_0 ^1 ((ln(2))/(1+t))+((ln(t))/(1+t))−((ln(1+t))/(1+t))dt =ln^2 (2)−((ln^2 (2))/2)+∫_0 ^1 ((ln(t))/(1+t))dt=((ln^2 (2))/2)+∫_0 ^1 ((ln(1−(−t))/(−t))d(−t) =((ln^2 (2))/2)−Li_2 (−1) B=−((ln^2 (2))/2)+Li_2 (−1) 2Ω=((ln^2 (2))/2)+((ln(2))/2)+(1/2)+A+B =((ln^2 (2))/2)+((ln(2))/2)+(1/2)−((ln(2))/2)−((ln^2 (2))/2)+Li_2 (−1) =(1/2)+Li_2 (−1)=(1/2)+(π^2 /(12))=(1/(12))(π^2 −6) Ω=(1/(24))(π^2 −6)](Q176545.png) | ||
| ||
Commented by Tawa11 last updated on 22/Sep/22 | ||
 | ||
Commented by Peace last updated on 23/Sep/22 | ||
 | ||