Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 176636 by cortano1 last updated on 23/Sep/22

{ ((p^3 +q^3 =r^2 )),((p^3 +r^3 =q^2 )),((q^3 +r^3 =p^2 )) :} ⇒20pqr =?

$$\:\begin{cases}{{p}^{\mathrm{3}} +{q}^{\mathrm{3}} ={r}^{\mathrm{2}} }\\{{p}^{\mathrm{3}} +{r}^{\mathrm{3}} ={q}^{\mathrm{2}} }\\{{q}^{\mathrm{3}} +{r}^{\mathrm{3}} ={p}^{\mathrm{2}} }\end{cases} \\ $$$$\:\Rightarrow\mathrm{20}{pqr}\:=? \\ $$

Commented by Frix last updated on 23/Sep/22

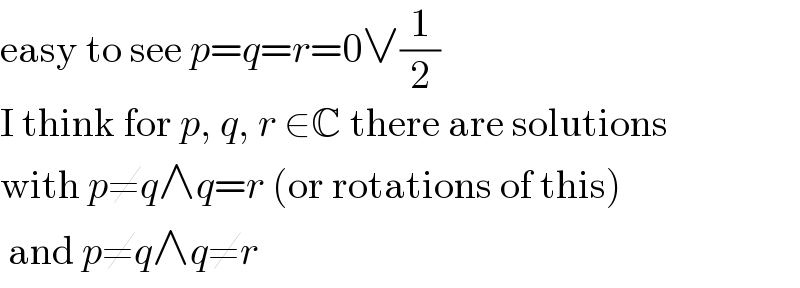
easy to see p=q=r=0∨(1/2) I think for p, q, r ∈C there are solutions with p≠q∧q=r (or rotations of this) and p≠q∧q≠r

$$\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:{p}={q}={r}=\mathrm{0}\vee\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{for}\:{p},\:{q},\:{r}\:\in\mathbb{C}\:\mathrm{there}\:\mathrm{are}\:\mathrm{solutions} \\ $$$$\mathrm{with}\:{p}\neq{q}\wedge{q}={r}\:\left(\mathrm{or}\:\mathrm{rotations}\:\mathrm{of}\:\mathrm{this}\right) \\ $$$$\:\mathrm{and}\:{p}\neq{q}\wedge{q}\neq{r} \\ $$

Commented by Frix last updated on 23/Sep/22

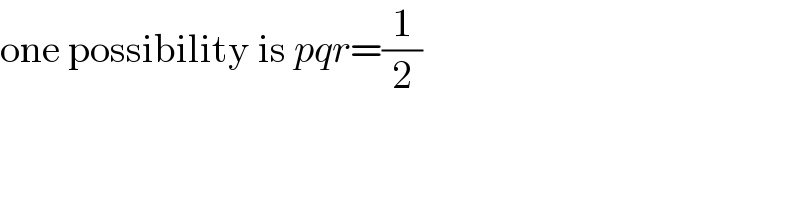
one possibility is pqr=(1/2)

$$\mathrm{one}\:\mathrm{possibility}\:\mathrm{is}\:{pqr}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Answered by BaliramKumar last updated on 23/Sep/22

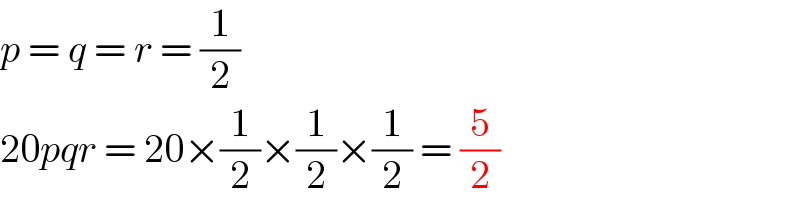
p = q = r = (1/2) 20pqr = 20×(1/2)×(1/2)×(1/2) = (5/2)

$${p}\:=\:{q}\:=\:{r}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{20}{pqr}\:=\:\mathrm{20}×\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}\:=\:\frac{\mathrm{5}}{\mathrm{2}} \\ $$

Commented by mr W last updated on 23/Sep/22

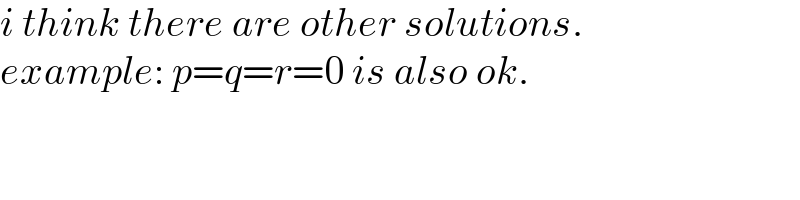
i think there are other solutions. example: p=q=r=0 is also ok.

$${i}\:{think}\:{there}\:{are}\:{other}\:{solutions}. \\ $$$${example}:\:{p}={q}={r}=\mathrm{0}\:{is}\:{also}\:{ok}. \\ $$

Answered by Rasheed.Sindhi last updated on 24/Sep/22

{ ((p^3 +q^3 =r^2 ...(i))),((p^3 +r^3 =q^2 ...(ii))),((q^3 +r^3 =p^2 ...(iii))) :} ; 20pqr =? (ii)⇒p^3 +(p^3 +q^3 )r=q^2 (iii)⇒q^3 +(p^3 +q^3 )r=p^2 r=((q^2 −p^3 )/(p^3 +q^3 ))=((p^2 −q^3 )/(p^3 +q^3 ))=±(√(p^3 +q^3 )) { ((q^2 −p^3 =p^2 −q^3 .....(A))),((p^2 −q^3 =±(p^3 +q^3 )^(3/2) ....(B))),((q^2 −p^3 =±(p^3 +q^3 )^(3/2) ....(C))) :} (A): q^2 −p^3 =p^2 −q^3 p^2 −q^2 +p^3 −q^3 =0 (p−q)(p+q)+(p−q)(p^2 +pq+q^2 )=0 (p−q)(p^2 +pq+q^2 +p+q)=0 p=q ∣ p^2 +pq+q^2 +p+q=0^★ In similar way q=r or p=q=r (i)⇒r^3 +r^3 =r^2 ⇒2r=1⇒r=(1/2) or p=q=r=(1/2) 20pqr=20(1/2)(1/2)(1/2)=5/2 p^2 +pq+q^2 +p+q=0 (p+q)^2 +(p+q)−pq=0 p+q=((−1±(√(1+4pq)))/2) (B): p^2 −q^3 =±(p^3 +q^3 )^(3/2) (p^2 −q^3 )^2 =(p^3 +q^3 )^3 p^4 −2p^2 q^3 +q^6 =p^9 +q^9 +3(pq)^3 (p^3 +q^3 ) (C): q^2 −p^3 =±(p^3 +q^3 )^(3/2) Continue...

$$\:\begin{cases}{{p}^{\mathrm{3}} +{q}^{\mathrm{3}} ={r}^{\mathrm{2}} ...\left({i}\right)}\\{{p}^{\mathrm{3}} +{r}^{\mathrm{3}} ={q}^{\mathrm{2}} ...\left({ii}\right)}\\{{q}^{\mathrm{3}} +{r}^{\mathrm{3}} ={p}^{\mathrm{2}} ...\left({iii}\right)}\end{cases}\:;\:\:\:\:\mathrm{20}{pqr}\:=? \\ $$$$\left({ii}\right)\Rightarrow{p}^{\mathrm{3}} +\left({p}^{\mathrm{3}} +{q}^{\mathrm{3}} \right){r}={q}^{\mathrm{2}} \\ $$$$\left({iii}\right)\Rightarrow{q}^{\mathrm{3}} +\left({p}^{\mathrm{3}} +{q}^{\mathrm{3}} \right){r}={p}^{\mathrm{2}} \\ $$$${r}=\frac{{q}^{\mathrm{2}} −{p}^{\mathrm{3}} }{{p}^{\mathrm{3}} +{q}^{\mathrm{3}} }=\frac{{p}^{\mathrm{2}} −{q}^{\mathrm{3}} }{{p}^{\mathrm{3}} +{q}^{\mathrm{3}} }=\pm\sqrt{{p}^{\mathrm{3}} +{q}^{\mathrm{3}} }\: \\ $$$$\begin{cases}{{q}^{\mathrm{2}} −{p}^{\mathrm{3}} ={p}^{\mathrm{2}} −{q}^{\mathrm{3}} .....\left({A}\right)}\\{{p}^{\mathrm{2}} −{q}^{\mathrm{3}} =\pm\left({p}^{\mathrm{3}} +{q}^{\mathrm{3}} \right)^{\mathrm{3}/\mathrm{2}} ....\left({B}\right)}\\{{q}^{\mathrm{2}} −{p}^{\mathrm{3}} =\pm\left({p}^{\mathrm{3}} +{q}^{\mathrm{3}} \right)^{\mathrm{3}/\mathrm{2}} ....\left({C}\right)}\end{cases} \\ $$$$\left({A}\right): \\ $$$${q}^{\mathrm{2}} −{p}^{\mathrm{3}} ={p}^{\mathrm{2}} −{q}^{\mathrm{3}} \\ $$$${p}^{\mathrm{2}} −{q}^{\mathrm{2}} +{p}^{\mathrm{3}} −{q}^{\mathrm{3}} =\mathrm{0} \\ $$$$\left({p}−{q}\right)\left({p}+{q}\right)+\left({p}−{q}\right)\left({p}^{\mathrm{2}} +{pq}+{q}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\left({p}−{q}\right)\left({p}^{\mathrm{2}} +{pq}+{q}^{\mathrm{2}} +{p}+{q}\right)=\mathrm{0} \\ $$$${p}={q}\:\mid\:{p}^{\mathrm{2}} +{pq}+{q}^{\mathrm{2}} +{p}+{q}=\mathrm{0}^{\bigstar} \\ $$$${In}\:{similar}\:{way}\:{q}={r} \\ $$$${or}\:\:{p}={q}={r} \\ $$$$\left({i}\right)\Rightarrow{r}^{\mathrm{3}} +{r}^{\mathrm{3}} ={r}^{\mathrm{2}} \Rightarrow\mathrm{2}{r}=\mathrm{1}\Rightarrow{r}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${or}\:\:{p}={q}={r}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{20}{pqr}=\mathrm{20}\left(\mathrm{1}/\mathrm{2}\right)\left(\mathrm{1}/\mathrm{2}\right)\left(\mathrm{1}/\mathrm{2}\right)=\mathrm{5}/\mathrm{2} \\ $$$$ \\ $$$${p}^{\mathrm{2}} +{pq}+{q}^{\mathrm{2}} +{p}+{q}=\mathrm{0} \\ $$$$\:\:\:\:\:\left({p}+{q}\right)^{\mathrm{2}} +\left({p}+{q}\right)−{pq}=\mathrm{0} \\ $$$$\:\:\:\:{p}+{q}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{4}{pq}}}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$$\left({B}\right): \\ $$$${p}^{\mathrm{2}} −{q}^{\mathrm{3}} =\pm\left({p}^{\mathrm{3}} +{q}^{\mathrm{3}} \right)^{\mathrm{3}/\mathrm{2}} \\ $$$$\left({p}^{\mathrm{2}} −{q}^{\mathrm{3}} \right)^{\mathrm{2}} =\left({p}^{\mathrm{3}} +{q}^{\mathrm{3}} \right)^{\mathrm{3}} \\ $$$${p}^{\mathrm{4}} −\mathrm{2}{p}^{\mathrm{2}} {q}^{\mathrm{3}} +{q}^{\mathrm{6}} ={p}^{\mathrm{9}} +{q}^{\mathrm{9}} +\mathrm{3}\left({pq}\right)^{\mathrm{3}} \left({p}^{\mathrm{3}} +{q}^{\mathrm{3}} \right) \\ $$$$\left({C}\right): \\ $$$${q}^{\mathrm{2}} −{p}^{\mathrm{3}} =\pm\left({p}^{\mathrm{3}} +{q}^{\mathrm{3}} \right)^{\mathrm{3}/\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{Continue}... \\ $$

Commented by Frix last updated on 24/Sep/22

it′s easier this way: q=αp∧r=βp { (((1+α^3 )p^3 =β^2 p^2 )),(((1+β^3 )p^3 =α^2 p^2 )),(((α^3 +β^3 )p^3 =p^2 )) :} first obvious solution p=0 ⇒ p=q=r=0 { ((p=(β^2 /(1+α^3 )))),((p=(α^2 /(1+β^3 )))),((p=(1/(α^3 +β^3 )))) :} second obvious solution α=β=1 ⇒ p=q=r=(1/2) now we have to solve (1/(α^3 +β^3 ))=(α^2 /(1+β^3 ))=(β^2 /(1+α^3 )) which is hard I think we get 19 pairs (α, β) including (1, 1) >and of course because we can exchange α and β 9 of the remaining 18 are unique if we set β=1 ⇒ α=1 and 2 pairs of complex solutions which I can only give approximately at the moment α=−.975564±.528237 α=.475564±1.18273 the equation is α^4 +α^3 +α^2 +2α+2=0 and has no useable exact solutions

$$\mathrm{it}'\mathrm{s}\:\mathrm{easier}\:\mathrm{this}\:\mathrm{way}: \\ $$$${q}=\alpha{p}\wedge{r}=\beta{p} \\ $$$$\begin{cases}{\left(\mathrm{1}+\alpha^{\mathrm{3}} \right){p}^{\mathrm{3}} =\beta^{\mathrm{2}} {p}^{\mathrm{2}} }\\{\left(\mathrm{1}+\beta^{\mathrm{3}} \right){p}^{\mathrm{3}} =\alpha^{\mathrm{2}} {p}^{\mathrm{2}} }\\{\left(\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} \right){p}^{\mathrm{3}} ={p}^{\mathrm{2}} }\end{cases} \\ $$$$\mathrm{first}\:\mathrm{obvious}\:\mathrm{solution}\:{p}=\mathrm{0}\:\Rightarrow\:{p}={q}={r}=\mathrm{0} \\ $$$$\begin{cases}{{p}=\frac{\beta^{\mathrm{2}} }{\mathrm{1}+\alpha^{\mathrm{3}} }}\\{{p}=\frac{\alpha^{\mathrm{2}} }{\mathrm{1}+\beta^{\mathrm{3}} }}\\{{p}=\frac{\mathrm{1}}{\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} }}\end{cases} \\ $$$$\mathrm{second}\:\mathrm{obvious}\:\mathrm{solution}\:\alpha=\beta=\mathrm{1}\:\Rightarrow\:{p}={q}={r}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{solve} \\ $$$$\frac{\mathrm{1}}{\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} }=\frac{\alpha^{\mathrm{2}} }{\mathrm{1}+\beta^{\mathrm{3}} }=\frac{\beta^{\mathrm{2}} }{\mathrm{1}+\alpha^{\mathrm{3}} } \\ $$$$\mathrm{which}\:\mathrm{is}\:\mathrm{hard} \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{we}\:\mathrm{get}\:\mathrm{19}\:\mathrm{pairs}\:\left(\alpha,\:\beta\right)\:\mathrm{including}\:\left(\mathrm{1},\:\mathrm{1}\right) \\ $$$$\:>\mathrm{and}\:\mathrm{of}\:\mathrm{course}\:\mathrm{because}\:\mathrm{we}\:\mathrm{can}\:\mathrm{exchange} \\ $$$$\alpha\:\mathrm{and}\:\beta\:\mathrm{9}\:\mathrm{of}\:\mathrm{the}\:\mathrm{remaining}\:\mathrm{18}\:\mathrm{are}\:\mathrm{unique} \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{set}\:\beta=\mathrm{1}\:\Rightarrow\:\alpha=\mathrm{1}\:\mathrm{and}\:\mathrm{2}\:\mathrm{pairs}\:\mathrm{of}\:\mathrm{complex} \\ $$$$\mathrm{solutions}\:\mathrm{which}\:\mathrm{I}\:\mathrm{can}\:\mathrm{only}\:\mathrm{give}\:\mathrm{approximately}\:\mathrm{at} \\ $$$$\mathrm{the}\:\mathrm{moment} \\ $$$$\alpha=−.\mathrm{975564}\pm.\mathrm{528237} \\ $$$$\alpha=.\mathrm{475564}\pm\mathrm{1}.\mathrm{18273} \\ $$$$\mathrm{the}\:\mathrm{equation}\:\mathrm{is}\:\alpha^{\mathrm{4}} +\alpha^{\mathrm{3}} +\alpha^{\mathrm{2}} +\mathrm{2}\alpha+\mathrm{2}=\mathrm{0}\:\mathrm{and} \\ $$$$\mathrm{has}\:\mathrm{no}\:\mathrm{useable}\:\mathrm{exact}\:\mathrm{solutions} \\ $$

Commented by Rasheed.Sindhi last updated on 24/Sep/22

Yes sir, you′re right! ThanX a lot!

$$\mathrm{Yes}\:\mathrm{sir},\:\mathrm{you}'\mathrm{re}\:\mathrm{right}!\: \\ $$$$\mathcal{T}{han}\mathcal{X}\:{a}\:{lot}! \\ $$

Commented by Frix last updated on 24/Sep/22

I get (α, β)= (1, β=α) (.475564±1.18273i,1) (.384646±.923064i, −.500000∓.333321i) [not sure if −(1/2)] (.292652±.727828i, β=α) (−.792652±.429196i, β=α) (−.975564±.528237i, 1) (−1.38465±.923064i, β=conj(α))

$$\mathrm{I}\:\mathrm{get}\:\left(\alpha,\:\beta\right)= \\ $$$$\left(\mathrm{1},\:\beta=\alpha\right) \\ $$$$\left(.\mathrm{475564}\pm\mathrm{1}.\mathrm{18273i},\mathrm{1}\right) \\ $$$$\left(.\mathrm{384646}\pm.\mathrm{923064i},\:−.\mathrm{500000}\mp.\mathrm{333321i}\right)\:\left[\mathrm{not}\:\mathrm{sure}\:\mathrm{if}\:−\frac{\mathrm{1}}{\mathrm{2}}\right] \\ $$$$\left(.\mathrm{292652}\pm.\mathrm{727828i},\:\beta=\alpha\right) \\ $$$$\left(−.\mathrm{792652}\pm.\mathrm{429196i},\:\beta=\alpha\right) \\ $$$$\left(−.\mathrm{975564}\pm.\mathrm{528237i},\:\mathrm{1}\right) \\ $$$$\left(−\mathrm{1}.\mathrm{38465}\pm.\mathrm{923064i},\:\beta=\mathrm{conj}\left(\alpha\right)\right) \\ $$

Commented by Tawa11 last updated on 25/Sep/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com