
Question Number 176668 by mnjuly1970 last updated on 24/Sep/22

Answered by a.lgnaoui last updated on 25/Sep/22
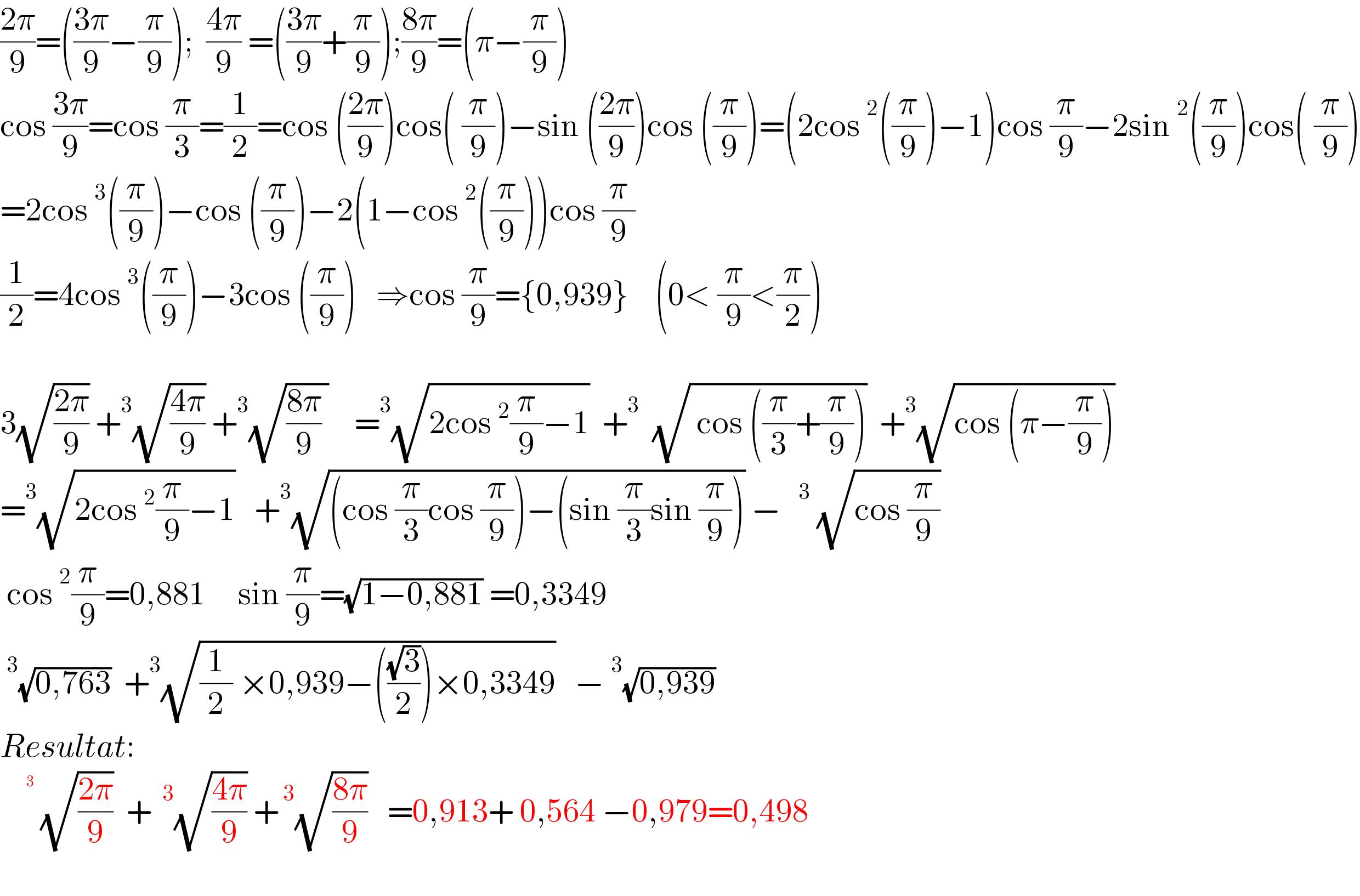
$$\frac{\mathrm{2}\pi}{\mathrm{9}}=\left(\frac{\mathrm{3}\pi}{\mathrm{9}}−\frac{\pi}{\mathrm{9}}\right);\:\:\frac{\mathrm{4}\pi}{\mathrm{9}}\:=\left(\frac{\mathrm{3}\pi}{\mathrm{9}}+\frac{\pi}{\mathrm{9}}\right);\frac{\mathrm{8}\pi}{\mathrm{9}}=\left(\pi−\frac{\pi}{\mathrm{9}}\right) \\ $$$$\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{9}}=\mathrm{cos}\:\frac{\pi}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{cos}\:\left(\frac{\mathrm{2}\pi}{\mathrm{9}}\right)\mathrm{cos}\left(\:\frac{\pi}{\mathrm{9}}\right)−\mathrm{sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{9}}\right)\mathrm{cos}\:\left(\frac{\pi}{\mathrm{9}}\right)=\left(\mathrm{2cos}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{9}}\right)−\mathrm{1}\right)\mathrm{cos}\:\frac{\pi}{\mathrm{9}}−\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{9}}\right)\mathrm{cos}\left(\:\frac{\pi}{\mathrm{9}}\right) \\ $$$$=\mathrm{2cos}\:^{\mathrm{3}} \left(\frac{\pi}{\mathrm{9}}\right)−\mathrm{cos}\:\left(\frac{\pi}{\mathrm{9}}\right)−\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{9}}\right)\right)\mathrm{cos}\:\frac{\pi}{\mathrm{9}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{4cos}\:^{\mathrm{3}} \left(\frac{\pi}{\mathrm{9}}\right)−\mathrm{3cos}\:\left(\frac{\pi}{\mathrm{9}}\right)\:\:\:\Rightarrow\mathrm{cos}\:\frac{\pi}{\mathrm{9}}=\left\{\mathrm{0},\mathrm{939}\right\}\:\:\:\:\left(\mathrm{0}<\:\frac{\pi}{\mathrm{9}}<\frac{\pi}{\mathrm{2}}\right) \\ $$$$ \\ $$$$\mathrm{3}\sqrt{\frac{\mathrm{2}\pi}{\mathrm{9}}}\:+^{\mathrm{3}} \sqrt{\frac{\mathrm{4}\pi}{\mathrm{9}}}\:+^{\mathrm{3}} \sqrt{\frac{\mathrm{8}\pi}{\mathrm{9}}\:}\:\:\:\:=^{\mathrm{3}} \sqrt{\mathrm{2cos}\:^{\mathrm{2}} \frac{\pi}{\mathrm{9}}−\mathrm{1}}\:\:+^{\mathrm{3}} \:\:\sqrt{\:\mathrm{cos}\:\left(\frac{\pi}{\mathrm{3}}+\frac{\pi}{\mathrm{9}}\right)}\:\:+^{\mathrm{3}} \sqrt{\mathrm{cos}\:\left(\pi−\frac{\pi}{\mathrm{9}}\right)} \\ $$$$=^{\mathrm{3}} \sqrt{\mathrm{2cos}\:^{\mathrm{2}} \frac{\pi}{\mathrm{9}}−\mathrm{1}}\:\:\:+^{\mathrm{3}} \sqrt{\left(\mathrm{cos}\:\frac{\pi}{\mathrm{3}}\mathrm{cos}\:\frac{\pi}{\mathrm{9}}\right)−\left(\mathrm{sin}\:\frac{\pi}{\mathrm{3}}\mathrm{sin}\:\frac{\pi}{\mathrm{9}}\right)}\:−^{\:\:\:\:\mathrm{3}} \:\sqrt{\mathrm{cos}\:\frac{\pi}{\mathrm{9}}} \\ $$$$\:\mathrm{cos}\:^{\mathrm{2}} \frac{\pi}{\mathrm{9}}=\mathrm{0},\mathrm{881}\:\:\:\:\:\mathrm{sin}\:\frac{\pi}{\mathrm{9}}=\sqrt{\mathrm{1}−\mathrm{0},\mathrm{881}}\:=\mathrm{0},\mathrm{3349} \\ $$$$\:^{\mathrm{3}} \sqrt{\mathrm{0},\mathrm{763}}\:\:+^{\mathrm{3}} \sqrt{\frac{\mathrm{1}}{\mathrm{2}}\:×\mathrm{0},\mathrm{939}−\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)×\mathrm{0},\mathrm{3349}}\:\:\:−\:^{\mathrm{3}} \sqrt{\mathrm{0},\mathrm{939}}\:\: \\ $$$${Resultat}: \\ $$$$\:\:^{\:\:^{\:\:\mathrm{3}} } \:\sqrt{\frac{\mathrm{2}\pi}{\mathrm{9}}}\:\:+\:^{\:\mathrm{3}} \sqrt{\frac{\mathrm{4}\pi}{\mathrm{9}}}\:+^{\:\mathrm{3}} \sqrt{\frac{\mathrm{8}\pi}{\mathrm{9}}}\:\:\:=\mathrm{0},\mathrm{913}+\:\mathrm{0},\mathrm{564}\:−\mathrm{0},\mathrm{979}=\mathrm{0},\mathrm{498} \\ $$$$ \\ $$
Answered by Peace last updated on 25/Sep/22

$${cos}\left(\frac{\mathrm{3}.\mathrm{2}\pi}{\mathrm{9}}\right)={cos}\left(\frac{\mathrm{3}.\mathrm{4}\pi}{\mathrm{9}}\right)={cos}\left(\frac{\mathrm{3}.\mathrm{8}\pi}{\mathrm{9}}\right)={cos}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${cos}\left(\mathrm{3}{x}\right)=−\frac{\mathrm{1}}{\mathrm{2}}\Leftrightarrow\mathrm{4}{cos}^{\mathrm{3}} \left({x}\right)−\mathrm{3}{cos}\left({x}\right)+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$$\frac{\mathrm{2}\pi}{\mathrm{9}};\frac{\mathrm{4}\pi}{\mathrm{9}};\frac{\mathrm{8}\pi}{\mathrm{9}}\:\:{Principal}\:{Solution} \\ $$$${let}\:{a}=\left({cos}\left(\frac{\mathrm{2}\pi}{\mathrm{9}}\right)\right)^{\frac{\mathrm{1}}{\mathrm{3}}} ,{b}=\left({cos}\left(\frac{\mathrm{4}\pi}{\mathrm{9}}\right)\right)^{\frac{\mathrm{1}}{\mathrm{3}}} ,{c}=\left({cos}\left(\frac{\mathrm{8}\pi}{\mathrm{9}}\right)\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${a}^{\mathrm{3}} ,{b}^{\mathrm{3}} ,{c}^{\mathrm{3}} \:{Roots}\:{of}\:\:\mathrm{4}{X}^{\mathrm{3}} −\mathrm{3}{X}+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} =\mathrm{0};\Sigma{a}^{\mathrm{3}} {b}^{\mathrm{3}} =−\frac{\mathrm{3}}{\mathrm{4}};\left({abc}\right)^{\mathrm{3}} =−\frac{\mathrm{1}}{\mathrm{8}} \\ $$$${Using} \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} =\left({x}+{y}+{z}\right)^{\mathrm{3}} −\mathrm{3}\left({x}+{y}+{z}\right)\left({xy}+{yz}+{zx}\right)+\mathrm{3}{xyz} \\ $$$$\Rightarrow\mathrm{0}=\left({a}+{b}+{c}\right)^{\mathrm{3}} −\mathrm{3}\left({a}+{b}+{c}\right)\left({ab}+{bc}+{ca}\right)+\mathrm{3}{abc} \\ $$$$\Sigma{a}^{\mathrm{3}} {b}^{\mathrm{3}} =\left(\Sigma{ab}\right)^{\mathrm{3}} −\mathrm{3}\left(\Sigma{ab}\right)\left({abc}\left({a}+{b}+{c}\right)\right)+\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} \\ $$$${a}+{b}+{c}={r} \\ $$$${ab}+{bc}+{ca}={s}\Rightarrow \\ $$$$\begin{cases}{{r}^{\mathrm{3}} −\mathrm{3}{rs}−\frac{\mathrm{3}}{\mathrm{2}}=\mathrm{0}}\\{−\frac{\mathrm{3}}{\mathrm{4}}={s}^{\mathrm{3}} +\frac{\mathrm{3}}{\mathrm{2}}{rs}+\frac{\mathrm{3}}{\mathrm{4}}}\end{cases} \\ $$$$\Leftrightarrow\begin{cases}{{s}=\frac{\mathrm{2}{r}^{\mathrm{3}} −\mathrm{3}}{\mathrm{6}{r}}}\\{{s}^{\mathrm{3}} +\frac{\mathrm{3}}{\mathrm{2}}{rs}+\frac{\mathrm{3}}{\mathrm{2}}=\mathrm{0}....\left({E}\right)}\end{cases} \\ $$$${r}^{\mathrm{3}} ={t}..\left({E}\right)\Leftrightarrow\left(\mathrm{2}{t}−\mathrm{3}\right)^{\mathrm{3}} +\mathrm{216}{t}.\frac{\mathrm{3}}{\mathrm{12}}\left(\mathrm{2}{t}−\mathrm{3}\right)+\mathrm{3}.\mathrm{108}{t}=\mathrm{0} \\ $$$$\mathrm{8}{t}^{\mathrm{3}} −\mathrm{36}{t}^{\mathrm{2}} −\mathrm{27}+\mathrm{54}{t}+\mathrm{108}{t}^{\mathrm{2}} −\mathrm{162}{t}+\mathrm{324}{t}=\mathrm{0} \\ $$$$\mathrm{8}{t}^{\mathrm{3}} +\mathrm{72}{t}^{\mathrm{2}} +\mathrm{216}{t}−\mathrm{27}=\mathrm{0} \\ $$$${Cardon}\:\Rightarrow{t}=\frac{\mathrm{3}}{\mathrm{2}}\left(\sqrt[{\mathrm{3}}]{\mathrm{9}}−\mathrm{2}\right) \\ $$$${r}={a}+{b}+{c}=\sqrt[{\mathrm{3}}]{{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{9}}\right)}+\sqrt[{\mathrm{3}}]{{cos}\left(\frac{\mathrm{4}\pi}{\mathrm{9}}\right)}+\sqrt[{\mathrm{3}}]{{cos}\left(\frac{\mathrm{8}\pi}{\mathrm{9}}\right)}=\sqrt[{\mathrm{3}}]{{t}} \\ $$$$=\sqrt[{\mathrm{3}}]{\frac{\mathrm{3}^{\frac{\mathrm{5}}{\mathrm{3}}} −\mathrm{6}}{\mathrm{2}}}\approx\mathrm{0}.\mathrm{49} \\ $$$$ \\ $$
Answered by Peace last updated on 25/Sep/22

$${hello}\:{sir}\:{happy}\:{to}\:{comback}\:{in}\:{this}\:{forum} \\ $$$${i}\:{lost}\:{my}\:{compt}\:{mindispower} \\ $$
