
Question and Answers Forum
Question Number 176676 by Rasheed.Sindhi last updated on 24/Sep/22

Answered by mr W last updated on 24/Sep/22

Commented by Rasheed.Sindhi last updated on 25/Sep/22
Commented by Tawa11 last updated on 25/Sep/22

Answered by mr W last updated on 24/Sep/22
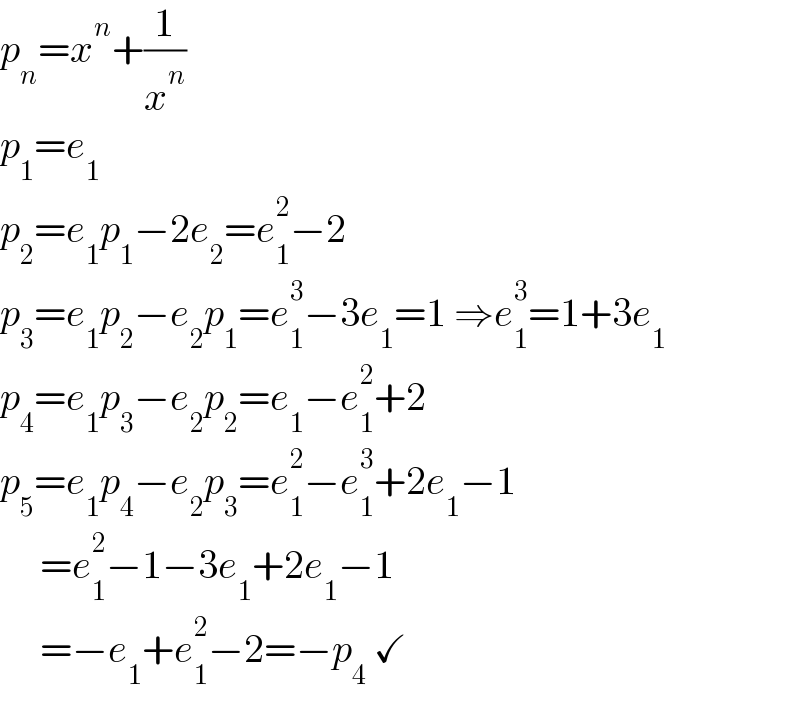
Commented by Rasheed.Sindhi last updated on 25/Sep/22

Commented by Tawa11 last updated on 25/Sep/22

Answered by Rasheed.Sindhi last updated on 25/Sep/22

Commented by mr W last updated on 25/Sep/22

