
Question and Answers Forum
Question Number 176679 by mnjuly1970 last updated on 24/Sep/22
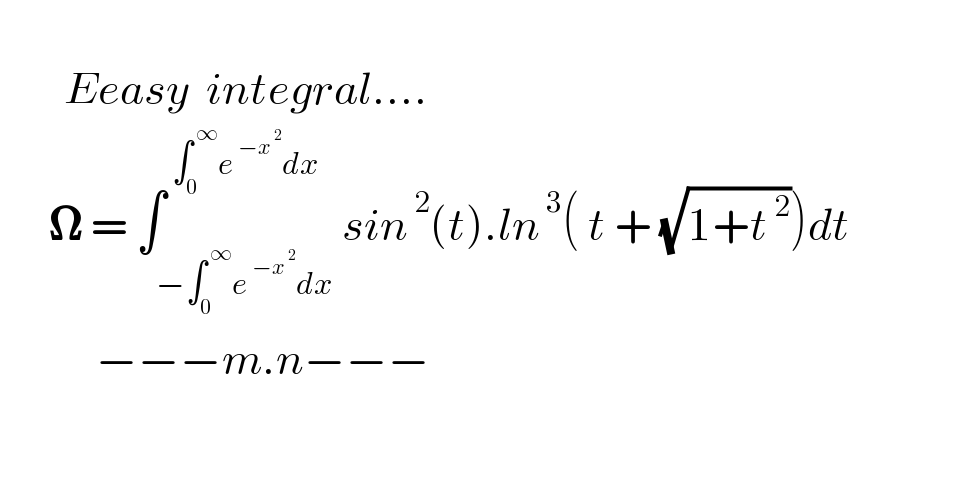
Answered by Peace last updated on 24/Sep/22
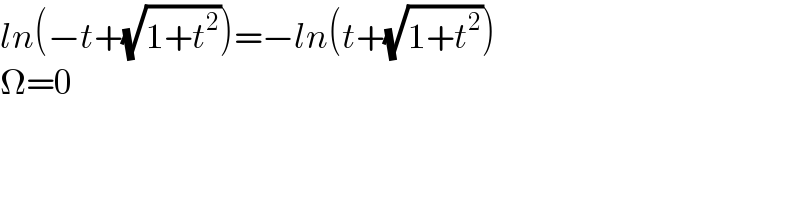
Answered by mahdipoor last updated on 25/Sep/22
![−f(a)=−[sin^2 (a).ln^3 (a+(√(a^2 +1)))]= sin^2 (a).[−ln(a+(√(a^2 +1)))]^3 = sin^2 (a).ln^3 ((1/(a+(√(a^2 +1)))))= sin^2 (a).ln^3 (((−a+(√(a^2 +1)))/([a+(√(a^2 +1))][−a+(√(a^2 +1))])))= sin^2 (−a).ln^3 (−a+(√((−a)^2 +1)))=f(−a) ⇒⇒ ∀a , f(ξ).δx+f(−ξ).δx=0 ⇒⇒ get ∫_0 ^∞ e^(−x^2 ) dx=m ξ_i =i.δx ⇒⇒ 0=lim_(δx→0) Σ_(i=0) ^(m/δx) f(−ξ_i ).δx+f(ξ_i ).δx= lim_(δx→0) Σ_(−m/δx) ^(m/δx) f(ξ_i ).δx=∫_( −m) ^( m) f(x)dx](Q176707.png)
| ||
Question and Answers Forum | ||
Question Number 176679 by mnjuly1970 last updated on 24/Sep/22 | ||
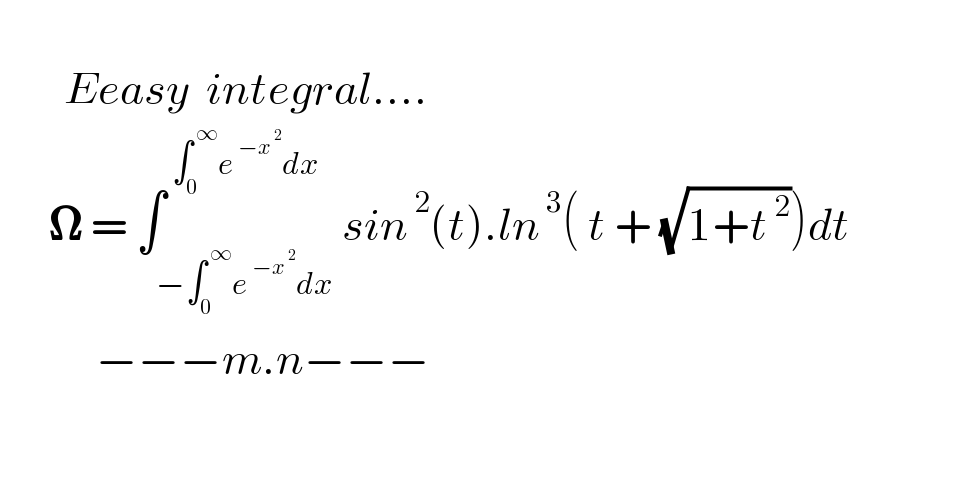 | ||
Answered by Peace last updated on 24/Sep/22 | ||
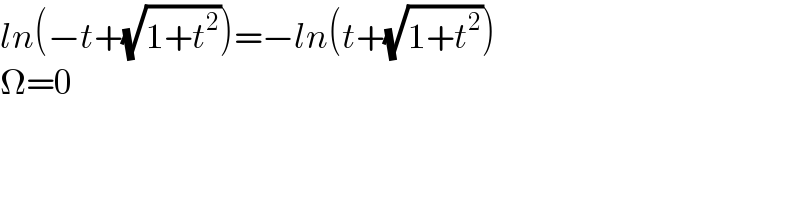 | ||
| ||
Answered by mahdipoor last updated on 25/Sep/22 | ||
![−f(a)=−[sin^2 (a).ln^3 (a+(√(a^2 +1)))]= sin^2 (a).[−ln(a+(√(a^2 +1)))]^3 = sin^2 (a).ln^3 ((1/(a+(√(a^2 +1)))))= sin^2 (a).ln^3 (((−a+(√(a^2 +1)))/([a+(√(a^2 +1))][−a+(√(a^2 +1))])))= sin^2 (−a).ln^3 (−a+(√((−a)^2 +1)))=f(−a) ⇒⇒ ∀a , f(ξ).δx+f(−ξ).δx=0 ⇒⇒ get ∫_0 ^∞ e^(−x^2 ) dx=m ξ_i =i.δx ⇒⇒ 0=lim_(δx→0) Σ_(i=0) ^(m/δx) f(−ξ_i ).δx+f(ξ_i ).δx= lim_(δx→0) Σ_(−m/δx) ^(m/δx) f(ξ_i ).δx=∫_( −m) ^( m) f(x)dx](Q176707.png) | ||
| ||