Question and Answers Forum

All Questions      Topic List

Mensuration Questions

Previous in All Question      Next in All Question      

Previous in Mensuration      Next in Mensuration      

Question Number 176946 by Ar Brandon last updated on 28/Sep/22

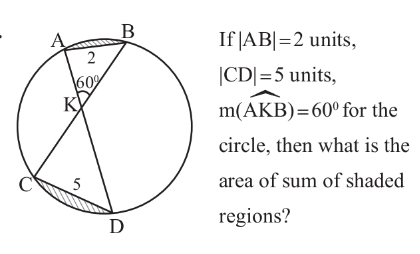
Answered by mr W last updated on 29/Sep/22

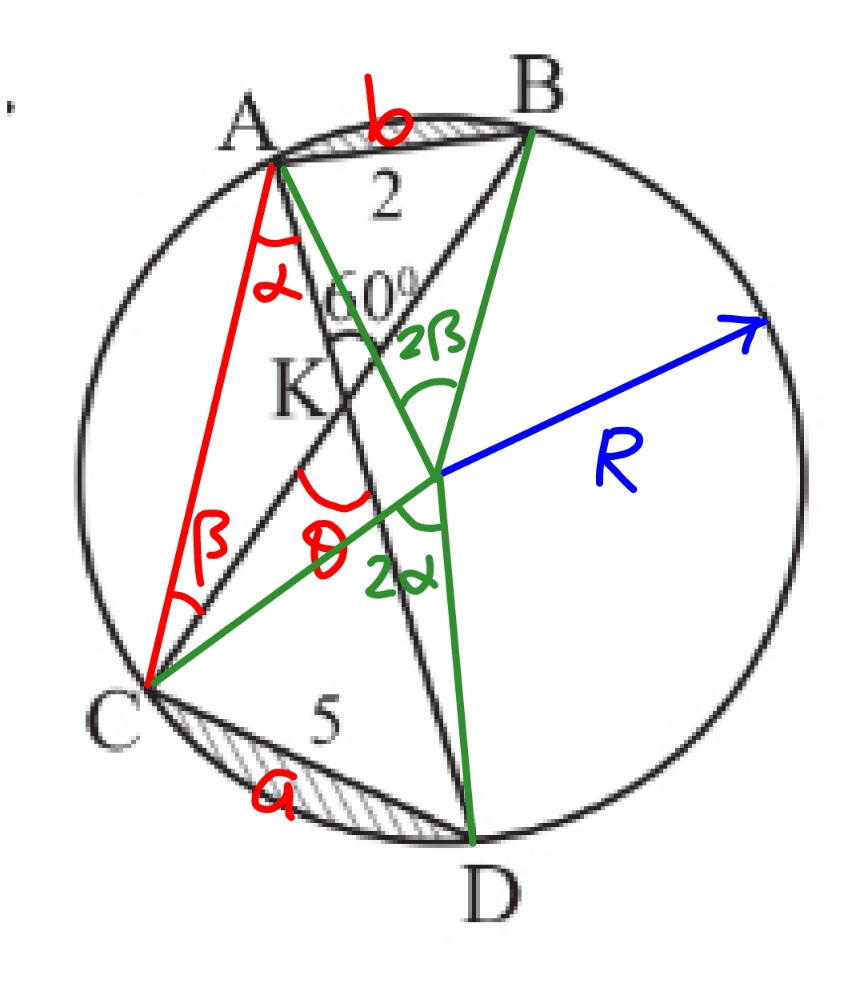
Commented by mr W last updated on 29/Sep/22

$$R=radius,K=diameterofcircle$$$$\sin \alpha =\frac{a}{2R}=\frac{a}{K}$$$$\sin \beta =\frac{b}{2R}=\frac{b}{K}$$$$\alpha +\beta =\theta =60°=\frac{\pi }{3}$$$$\cos (\alpha +\beta )=\cos \theta =\frac{1}{2}$$$$\sqrt{(1-\frac{a^2}{K^2})(1-\frac{b^2}{K^2})}-\frac{a}{K}\times \frac{b}{K}=\cos \theta$$$$(1-\frac{a^2}{K^2})(1-\frac{b^2}{K^2})={(\frac{ab}{K^2}+\cos \theta )}^2$$$$1-\frac{a^2}{K^2}-\frac{b^2}{K^2}=2\cos \theta \frac{ab}{K^2}+{\cos }^2\theta$$$$K^2=4R^2=\frac{a^2+b^2+2ab\cos \theta }{{\sin }^2\theta }$$$$\Rightarrow R=\frac{\sqrt{a^2+b^2+2ab\cos \theta }}{2\sin \theta }$$$$=\frac{\sqrt{2^2+5^2+2\times 2\times 5\times \frac{1}{2}}}{2\times \frac{\sqrt{3}}{2}}=\sqrt{13}$$$$A_{segment,a}=\alpha R^2-\frac{a}{2}\sqrt{R^2-\frac{a^2}{4}}$$$$A_{segment,b}=\beta R^2-\frac{b}{2}\sqrt{R^2-\frac{b^2}{4}}$$$$A_{shaded}=R^2\theta -\frac{a}{2}\sqrt{R^2-\frac{a^2}{4}}-\frac{b}{2}\sqrt{R^2-\frac{b^2}{4}}$$$$=13\times \frac{\pi }{3}-\frac{5}{2}\sqrt{13-\frac{5^2}{4}}-\frac{2}{2}\sqrt{13-\frac{2^2}{4}}$$$$=\frac{13\pi }{3}-\frac{23\sqrt{3}}{4}$$$$\approx 3.654$$

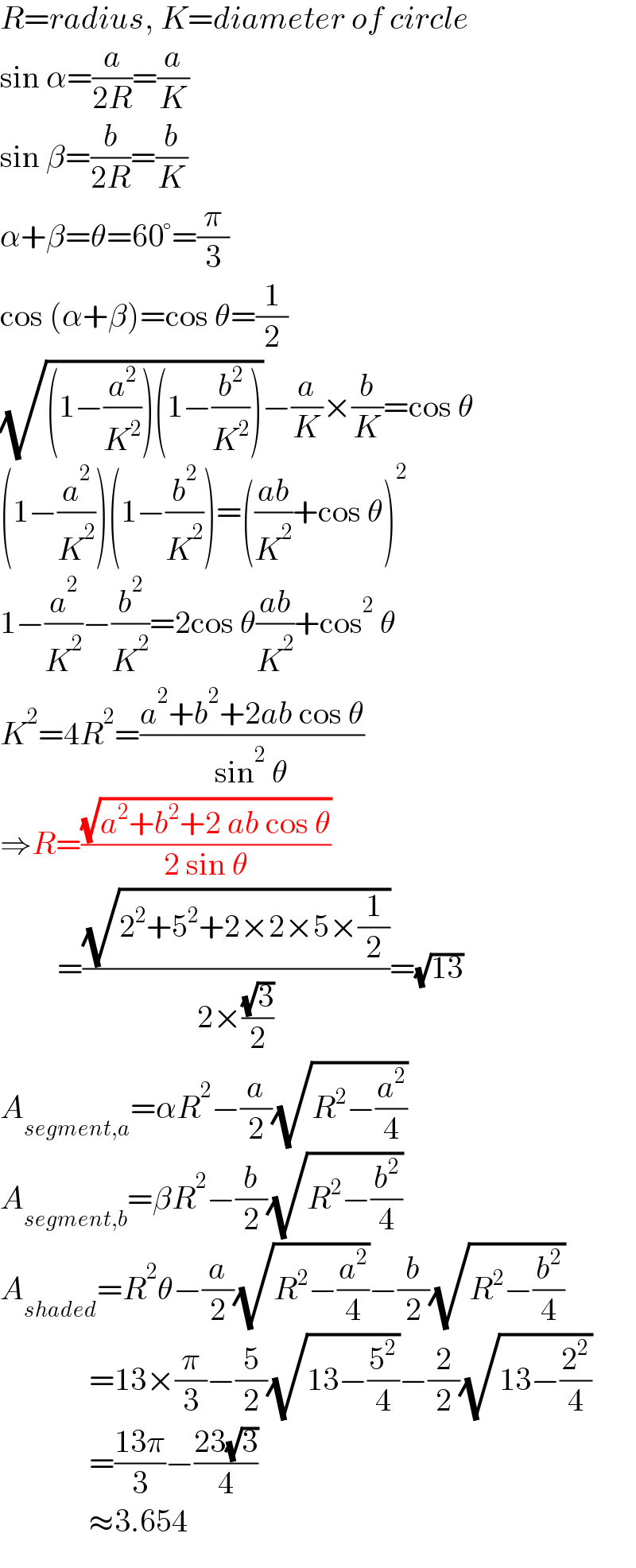
Commented by Ar Brandon last updated on 29/Sep/22

Thank you, Sir!

Commented by Tawa11 last updated on 02/Oct/22

$$\mathrm{Great}\mathrm{sir}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com