
Question and Answers Forum
Question Number 176963 by Ml last updated on 28/Sep/22

Commented by Frix last updated on 29/Sep/22
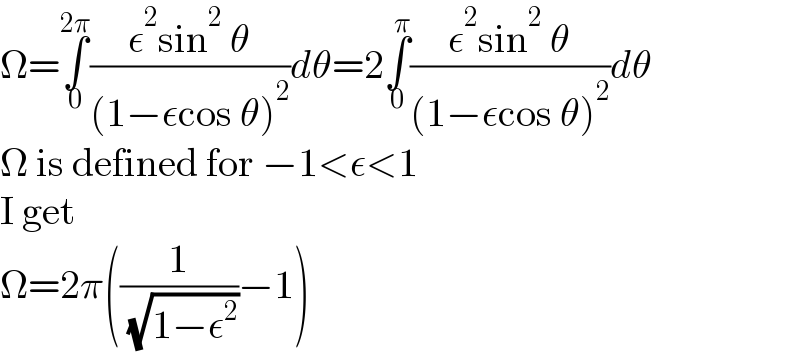
Answered by Ar Brandon last updated on 28/Sep/22
![I=∫_0 ^(2π) ((ξ^2 sin^2 ϑ)/((1−ξcosϑ)^2 ))dϑ =∫_0 ^(2π) ((ξsinϑ)/((1−ξcosϑ)^2 ))∙ξsinϑdϑ =[−((ξsinϑ)/(1−ξcosϑ))]_0 ^(2π) +∫_0 ^(2π) ((ξcosϑ)/(1−ξcosϑ))dϑ =∫_0 ^(2π) ((1/(1−ξcosϑ))−1)dϑ=∫_0 ^(2π) (1/(1−ξcosϑ))−2π J=∫(1/(1−ξcosϑ))dϑ=∫(1/(1−ξ(((1−t^2 )/(1+t^2 )))))∙(2/(1+t^2 ))dt, t=tan(ϑ/2) =∫(2/(1+t^2 −ξ(1+t^2 )))dt=∫(2/((1−ξ)t^2 +(1−ξ)))dt =(2/(1−ξ))∫(1/(t^2 +1))dt=(2/(1−ξ))(arctan(t))+C =(2/(1−ξ))(arctan(tan((ϑ/2))))+C](Q176970.png)
| ||
Question and Answers Forum | ||
Question Number 176963 by Ml last updated on 28/Sep/22 | ||
 | ||
Commented by Frix last updated on 29/Sep/22 | ||
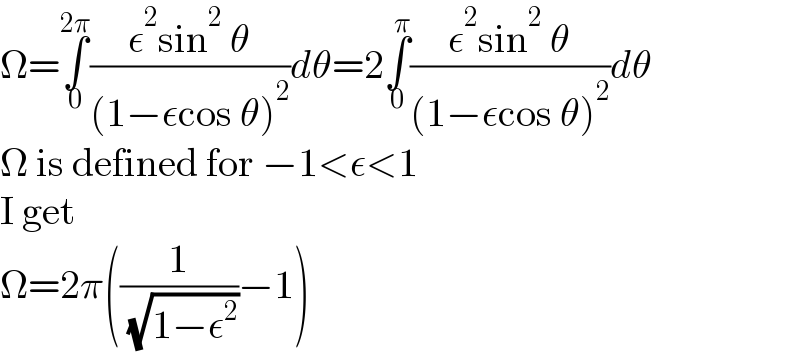 | ||
Answered by Ar Brandon last updated on 28/Sep/22 | ||
![I=∫_0 ^(2π) ((ξ^2 sin^2 ϑ)/((1−ξcosϑ)^2 ))dϑ =∫_0 ^(2π) ((ξsinϑ)/((1−ξcosϑ)^2 ))∙ξsinϑdϑ =[−((ξsinϑ)/(1−ξcosϑ))]_0 ^(2π) +∫_0 ^(2π) ((ξcosϑ)/(1−ξcosϑ))dϑ =∫_0 ^(2π) ((1/(1−ξcosϑ))−1)dϑ=∫_0 ^(2π) (1/(1−ξcosϑ))−2π J=∫(1/(1−ξcosϑ))dϑ=∫(1/(1−ξ(((1−t^2 )/(1+t^2 )))))∙(2/(1+t^2 ))dt, t=tan(ϑ/2) =∫(2/(1+t^2 −ξ(1+t^2 )))dt=∫(2/((1−ξ)t^2 +(1−ξ)))dt =(2/(1−ξ))∫(1/(t^2 +1))dt=(2/(1−ξ))(arctan(t))+C =(2/(1−ξ))(arctan(tan((ϑ/2))))+C](Q176970.png) | ||
| ||