
Question and Answers Forum
Question Number 177037 by mr W last updated on 30/Sep/22

Answered by Rasheed.Sindhi last updated on 30/Sep/22

Commented by mr W last updated on 30/Sep/22

Commented by Rasheed.Sindhi last updated on 30/Sep/22

Commented by Frix last updated on 30/Sep/22

Commented by mr W last updated on 30/Sep/22
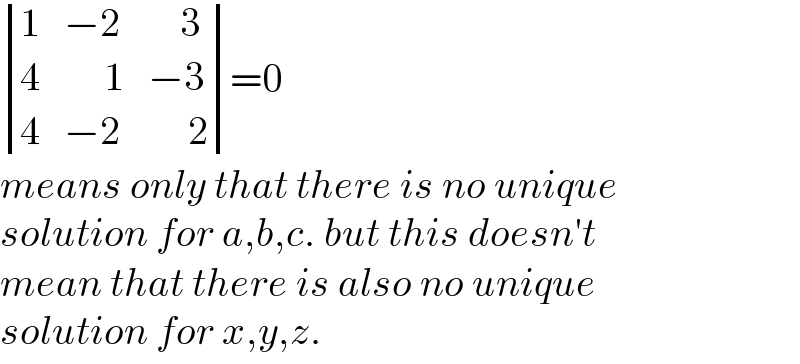
Commented by Rasheed.Sindhi last updated on 30/Sep/22

Commented by Rasheed.Sindhi last updated on 30/Sep/22
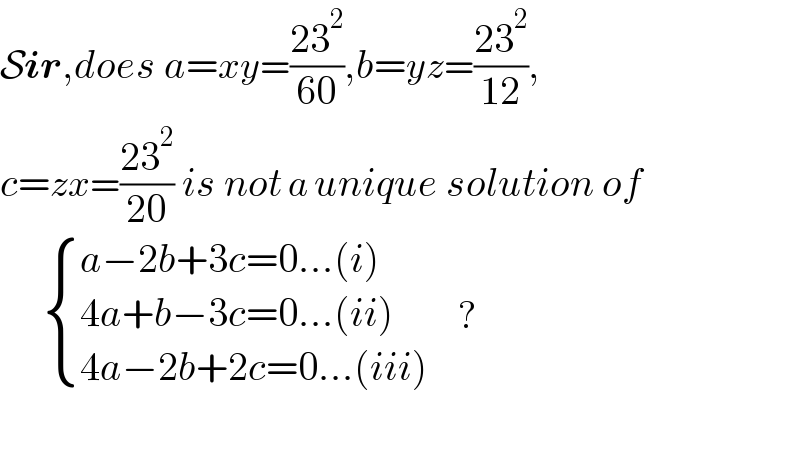
Commented by Frix last updated on 30/Sep/22
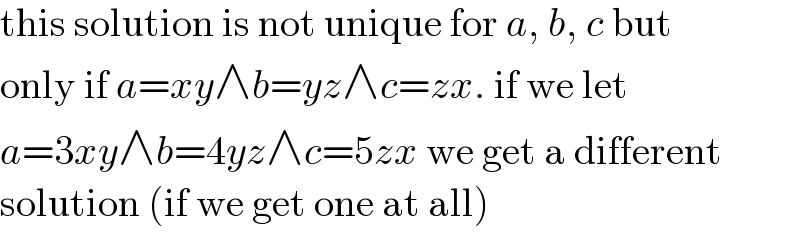
Commented by Tawa11 last updated on 02/Oct/22

Answered by mr W last updated on 30/Sep/22
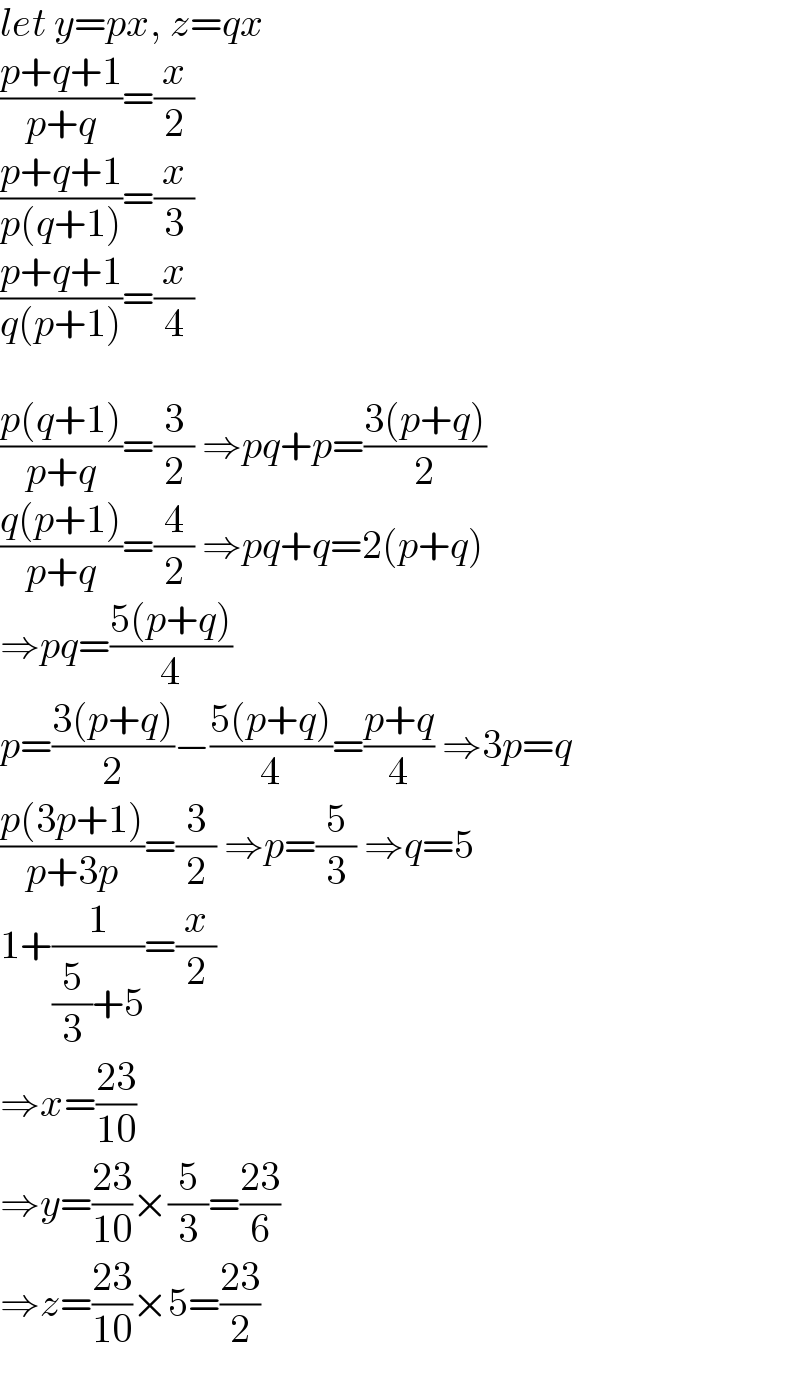
Answered by mr W last updated on 30/Sep/22
![an other way: ((x+y+z)/(xy+zx))=(1/2) ⇒xy+zx=2(x+y+z) ...(i) similarly ⇒yz+xy=3(x+y+z) ...(ii) ⇒zx+yz=4(x+y+z) ...(iii) [(i)+(ii)+(iii)]/2: xy+yz+zx=((9(x+y+z))/2) ...(iv) (iv)−(i): yz=((5(x+y+z))/2)=5λ with λ=((x+y+z)/2) similarly zx=((3(x+y+z))/2)=3λ xy=((x+y+z)/2)=λ (xyz)^2 =15λ^3 ⇒xyz=(√(15λ^3 )) ⇒x=((√(15λ))/5) ⇒y=((√(15λ))/3) ⇒z=((√(15λ))/1) x+y+z=2λ=((1/5)+(1/3)+1)(√(15λ)) ⇒(√(15λ))=((23)/2) ⇒x=((23)/(2×5))=((23)/(10)) ⇒y=((23)/(2×3))=((23)/6) ⇒z=((23)/2)](Q177086.png)
