solve (√(25−x^3 ))+(√(144−x^3 ))=13


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 177176 by mr W last updated on 01/Oct/22

$s o l v e$ $\sqrt{25 - x^{3}} + \sqrt{144 - x^{3}} = 13$
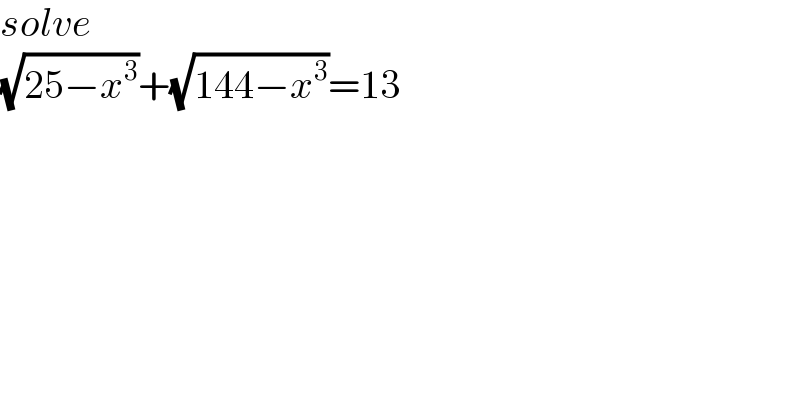
	Answered by a.lgnaoui last updated on 02/Oct/22

	$p o s o n s x^{3} = X$ ${(\sqrt{25 - X} + \sqrt{144 - X})}^{2} = 13^{2}$ $25 - X + 144 - X + 2 \sqrt{(25 - X) (144 - X)} = 169$ $169 - 2 X + 2 \sqrt{X^{2} - 169 X + 3600} = 169$ $\sqrt{X^{2} - 169 X + 3600} = X$ $X^{2} - 169 X + 3600 = X^{2}$ $169 X = 3600 \Rightarrow$ $169 X = 3600 \Rightarrow x =^{3} \sqrt{\frac{3600}{169}} = 2, 77$
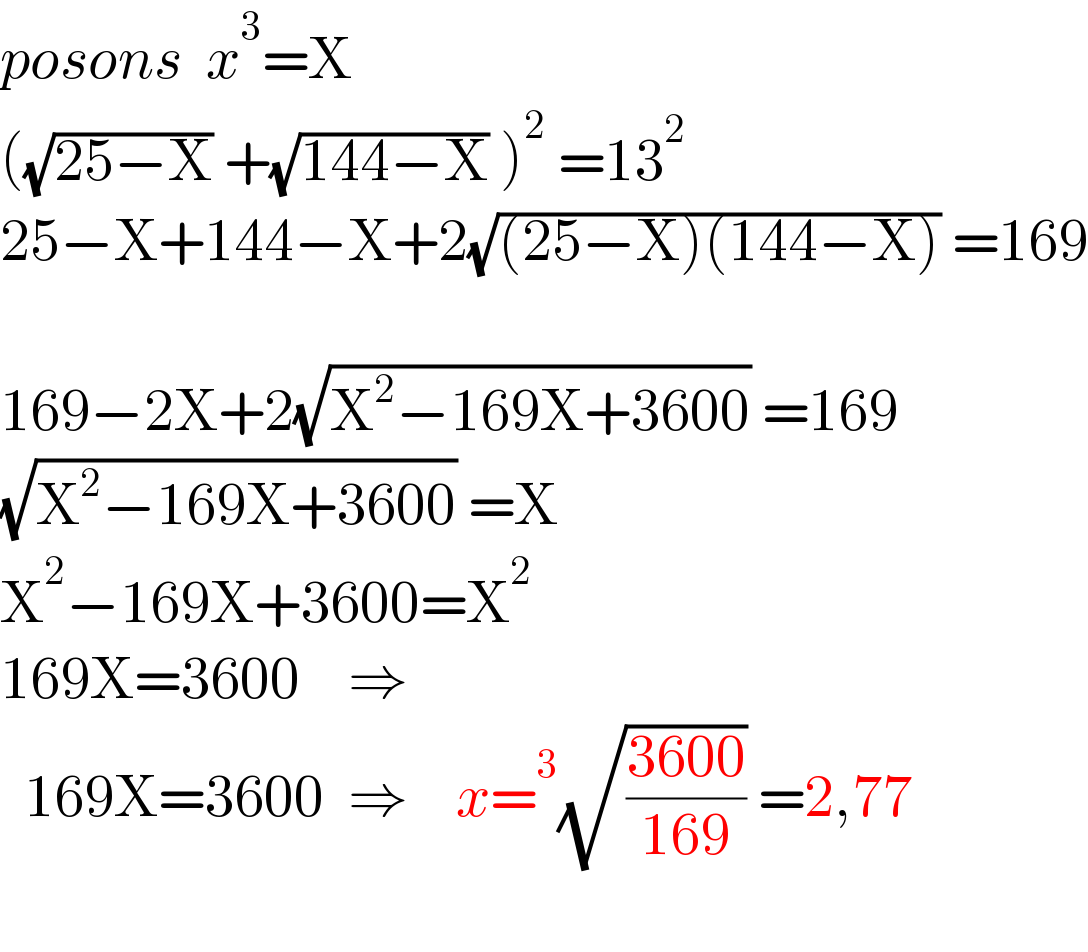
	Answered by Ar Brandon last updated on 02/Oct/22

	$\sqrt{25 - x^{3}} + \sqrt{144 - x^{3}} = 13, ∣ x ∣⩽ \sqrt[3]{25}$ $\sqrt{25 - x^{3}} = 13 - \sqrt{144 - x^{3}}$ $25 - x^{3} = 169 - 26 \sqrt{144 - x^{3}} + (144 - x^{3})$ $26 \sqrt{144 - x^{3}} = 288$ $676 (144 - x^{3}) = 82944$ $\Rightarrow 676 x^{3} = 14400$ $\Rightarrow x^{3} = \frac{3600}{169} \Rightarrow x = \sqrt[3]{\frac{3600}{169}}$
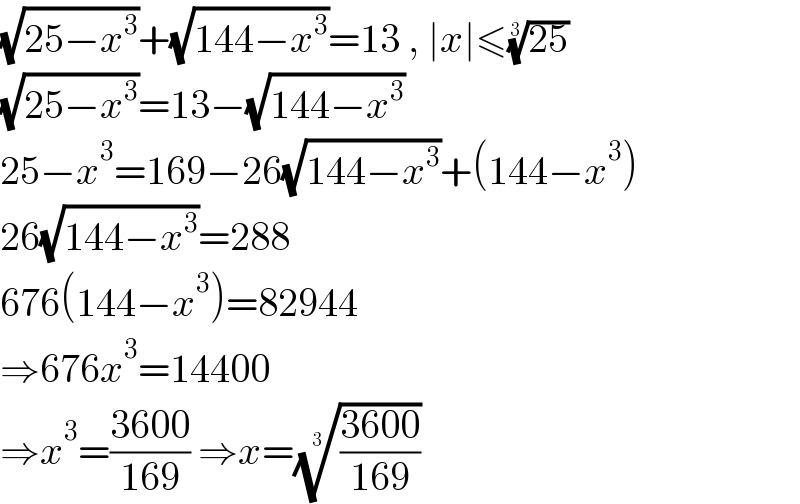
	Commented by Frix last updated on 02/Oct/22

	$x_{1} = \sqrt[3]{\frac{3600}{169}}; x_{2} = ω x_{1}; x_{3} = ω^{2} x_{1} with ω = - \frac{1}{2} + \frac{\sqrt{3}}{2} i$
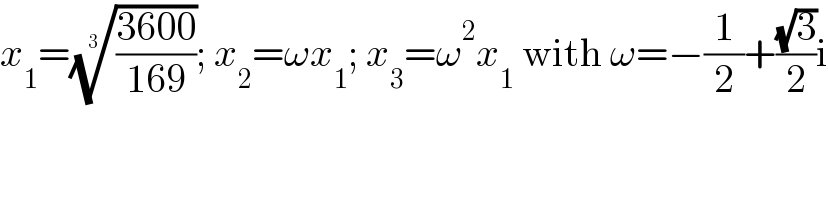
	Commented by Ar Brandon last updated on 02/Oct/22
	Thanks for completing
	Answered by mr W last updated on 02/Oct/22

	$l e t x^{3} = t^{2}$ $\sqrt{5^{2} - t^{2}} + \sqrt{12^{2} - t^{2}} = 13$ $t i s t h e a l t i t u d e o f r i g h t t r i a n g l e$ $\frac{1}{2} \times 13 \times t = \frac{1}{2} \times 5 \times 12$ $\Rightarrow t = \frac{5 \times 12}{13} = \frac{60}{13}$ $\Rightarrow x = \sqrt[3]{t^{2}} = \sqrt[3]{\frac{3600}{169}} \approx 2.772$
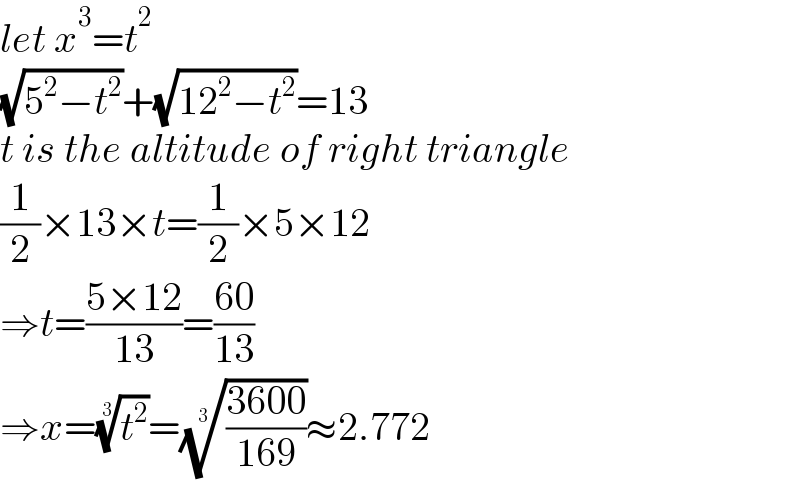
	Commented by mr W last updated on 02/Oct/22

	Commented by Rasheed.Sindhi last updated on 02/Oct/22

	$D e e p t h i n k i n g! I t^{'} s o n l y y o u s i r w h o$ $c a n s e e s u c h c o n n e c t k o n s!$
	Commented by mr W last updated on 02/Oct/22

	$t h a n k s s i r! d u e t o m y l o v e f o r g e o m e t r y$ $i t r y a t f i r s t, i f p o s s i b l e, t o s o l v e a$ $p r o b l e m g e o m e t r i c a l l y, s o m e t i m e s$ $w i t h s u c c e s s, s o m e t i m e s n o t .$
	Commented by Ar Brandon last updated on 02/Oct/22
	Sir how can I master geometry too?��
	Commented by mr W last updated on 02/Oct/22

	$i t h i n k w h e n y o u l o v e i t, y o u m a s t e r i t!$
	Commented by Ar Brandon last updated on 02/Oct/22

	$Sir, how do we call the type of geometry$ $which you often solve ?$ $For example in Calculus this \int_{0}^{1} \frac{\ln^{4} x}{1 + x + x^{2}} d x is integration .$ $But it falls under the advanced part called ‘ ‘ special {functions}^{″} .$ $I feel the geometry you solve is very much advanced$ $than the coordinate geometry most of us saw in$ $secondary school . Does it have a name, Sir ?$
	Commented by mr W last updated on 02/Oct/22

	$i {d o n}^{'} t k n o w a n y ‘ ‘ {a d v a n c e d}^{″} g e o m e t r y .$ $w h a t i k n o w i s t h a t w h a t p e o p l e$ $l e a r n i n t h e s c h o o l : g e o m e t r y a n d$ $a n a l y t i c g e o m e t r y .$
	Commented by Ar Brandon last updated on 02/Oct/22
	OK thanks
	Answered by Rasheed.Sindhi last updated on 02/Oct/22
	$(√(25−x^3 )) +(√(144−x^3 ))=13 (√(144−x^3 )) =a , (√(25−x^3 )) =b { ((a+b=13...(i))),((a^2 −b^2 =119)) :} ⇒((a^2 −b^2 )/(a+b))=((119)/(13)) ⇒a−b=((119)/(13))...(ii) (i)+(ii):2a=13+((119)/(13))=((288)/(13)) a=((144)/(13))⇒b=13−((144)/(13))=((25)/(13)) (√(25−x^3 )) =((25)/(13)) 25−x^3 =((625)/(169))⇒x^3 =25−((625)/(169))=((3600)/(169)) x=(((3600)/(169)))^(1/3) , (((3600)/(169)))^(1/3) ω , (((3600)/(169)))^(1/3) ω^2$
	$\sqrt{25 - x^{3}} + \sqrt{144 - x^{3}} = 13$ $\sqrt{144 - x^{3}} = a, \sqrt{25 - x^{3}} = b$ ${\begin{cases} a + b = 13 . . . (i) \\ a^{2} - b^{2} = 119 \end{cases} \Rightarrow \frac{a^{2} - b^{2}}{a + b} = \frac{119}{13}$ $\Rightarrow a - b = \frac{119}{13} . . . (i i)$ $(i) + (i i) : 2 a = 13 + \frac{119}{13} = \frac{288}{13}$ $a = \frac{144}{13} \Rightarrow b = 13 - \frac{144}{13} = \frac{25}{13}$ $\sqrt{25 - x^{3}} = \frac{25}{13}$ $25 - x^{3} = \frac{625}{169} \Rightarrow x^{3} = 25 - \frac{625}{169} = \frac{3600}{169}$ $x = \sqrt[3]{\frac{3600}{169}}, \sqrt[3]{\frac{3600}{169}} ω, \sqrt[3]{\frac{3600}{169}} ω^{2}$
	Answered by Rasheed.Sindhi last updated on 02/Oct/22

	$\sqrt{25 - x^{3}} + \sqrt{144 - x^{3}} = 13 . . . (i)$ $(\sqrt{25 - x^{3}} + \sqrt{144 - x^{3}}) (\sqrt{25 - x^{3}} - \sqrt{144 - x^{3}})$ $= 13 (\sqrt{25 - x^{3}} - \sqrt{144 - x^{3}})$ $13 (\sqrt{25 - x^{3}} - \sqrt{144 - x^{3}})$ $= (25 - x^{3}) - (144 - x^{3})$ $\sqrt{25 - x^{3}} - \sqrt{144 - x^{3}} = \frac{- 119}{13} . . . (i i)$ $(i) + (i i) :$ $2 \sqrt{25 - x^{3}} = 13 - \frac{119}{13} = \frac{50}{13}$ $25 - x^{3} = {(\frac{25}{13})}^{2} = \frac{625}{169}$ $x^{3} = 25 - \frac{625}{169} = \frac{3600}{169}$ $x = \sqrt[3]{\frac{3600}{169}}, \sqrt[3]{\frac{3600}{169}} ω, \sqrt[3]{\frac{3600}{169}} ω^{2}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum