
Question and Answers Forum
Question Number 177298 by peter frank last updated on 03/Oct/22
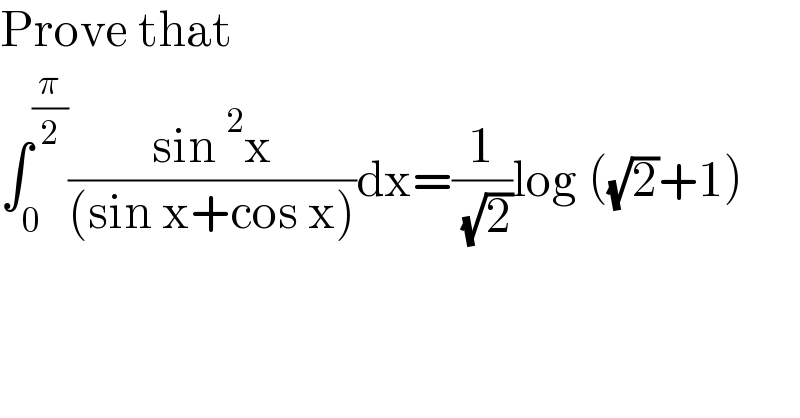
Answered by Ar Brandon last updated on 11/Oct/22
![I=∫_0 ^(π/2) ((sin^2 x)/(sinx+cosx))dx ...eqn(i) I=∫_0 ^(π/2) ((cos^2 x)/(sinx+cosx))dx ...eqn(ii) [letting t=(π/2)−x] eqn(i)+eqn(ii) ⇒ 2I=∫_0 ^(π/2) ((sin^2 x+cos^2 x)/(sinx+cosx))dx=∫_0 ^(π/2) (1/(sinx+cosx))dx I=(1/2)∫_0 ^(π/2) (1/(sinx+cosx))dx=(1/2)∫_0 ^1 (1/(((2t)/(1+t^2 ))+((1−t^2 )/(1+t^2 ))))∙(2/(1+t^2 ))dt =∫_0 ^1 (1/(1+2t−t^2 ))dt=∫_0 ^1 (dt/(2−(t−1)^2 ))=(1/( (√2)))[argth(((t−1)/( (√2))))]_0 ^1 =(1/(2(√2)))[ln∣((t+(√2)−1)/(t−(√2)−1))∣]_0 ^1 =(1/(2(√2)))ln∣(((√2)+1)/( (√2)−1))∣=(1/(2(√2)))ln((√2)+1)^2 =(1/( (√2)))ln((√2)+1)](Q177299.png)
Commented by peter frank last updated on 03/Oct/22

| ||
Question and Answers Forum | ||
Question Number 177298 by peter frank last updated on 03/Oct/22 | ||
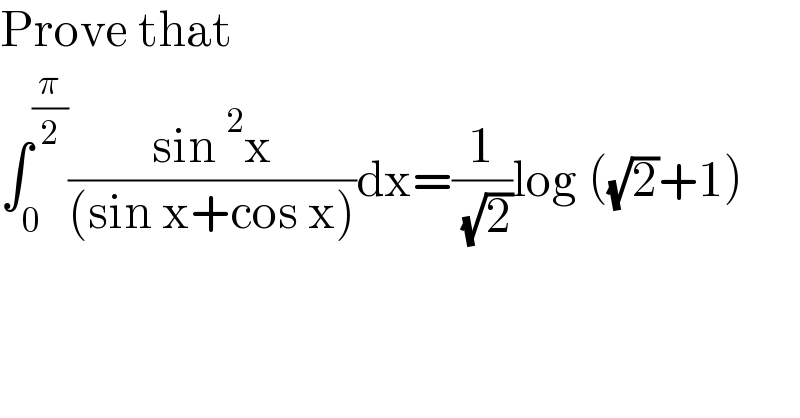 | ||
Answered by Ar Brandon last updated on 11/Oct/22 | ||
![I=∫_0 ^(π/2) ((sin^2 x)/(sinx+cosx))dx ...eqn(i) I=∫_0 ^(π/2) ((cos^2 x)/(sinx+cosx))dx ...eqn(ii) [letting t=(π/2)−x] eqn(i)+eqn(ii) ⇒ 2I=∫_0 ^(π/2) ((sin^2 x+cos^2 x)/(sinx+cosx))dx=∫_0 ^(π/2) (1/(sinx+cosx))dx I=(1/2)∫_0 ^(π/2) (1/(sinx+cosx))dx=(1/2)∫_0 ^1 (1/(((2t)/(1+t^2 ))+((1−t^2 )/(1+t^2 ))))∙(2/(1+t^2 ))dt =∫_0 ^1 (1/(1+2t−t^2 ))dt=∫_0 ^1 (dt/(2−(t−1)^2 ))=(1/( (√2)))[argth(((t−1)/( (√2))))]_0 ^1 =(1/(2(√2)))[ln∣((t+(√2)−1)/(t−(√2)−1))∣]_0 ^1 =(1/(2(√2)))ln∣(((√2)+1)/( (√2)−1))∣=(1/(2(√2)))ln((√2)+1)^2 =(1/( (√2)))ln((√2)+1)](Q177299.png) | ||
| ||
Commented by peter frank last updated on 03/Oct/22 | ||
 | ||