Question and Answers Forum

All Questions      Topic List

Mechanics Questions

Previous in All Question      Next in All Question      

Previous in Mechanics      Next in Mechanics      

Question Number 177332 by mr W last updated on 03/Oct/22

Commented by mr W last updated on 04/Oct/22

$$thequestionistofindthemaximum$$$$valueofxsuchthattherod{doesn}^{\prime }t$$$$slip.$$$$\left[Q90331\right]$$

Answered by mr W last updated on 04/Oct/22

Commented by mr W last updated on 04/Oct/22

Commented by mr W last updated on 04/Oct/22

$$let\xi =\frac{x}{l},\lambda =\frac{a}{l},\eta =\frac{h}{l}$$$$c=\sqrt{a^2+x^2}=l\sqrt{{\lambda }^2+{\xi }^2}$$$$\sin \varphi =\frac{a}{c}=\frac{\lambda }{\sqrt{{\lambda }^2+{\xi }^2}}$$$$$$$$\tan {\theta }_1⩽\mu$$$$\phi =\frac{\pi }{2}-{\theta }_2$$$$\tan \phi =\frac{1}{\tan {\theta }_2}⩾\frac{1}{\mu }$$$$\Rightarrow \cos \phi ⩽\frac{\mu }{\sqrt{1+{\mu }^2}}$$$$\tan \beta =\frac{c}{h}=\frac{\sqrt{{\lambda }^2+{\xi }^2}}{\eta }$$$$\sin \delta \times \sin \varphi =\cos \phi$$$$\Rightarrow \sin \delta =\frac{\cos \phi }{\sin \varphi }⩽\frac{\mu \sqrt{{\lambda }^2+{\xi }^2}}{\lambda \sqrt{1+{\mu }^2}}$$$$\Rightarrow \tan \delta ⩽\frac{\mu \sqrt{{\lambda }^2+{\xi }^2}}{\sqrt{{\lambda }^2-{\xi }^2}}(?)$$$$$$$$\frac{CD}{CB}=\frac{\sin (\beta +\delta )}{\sin \delta }=\frac{\sin \beta }{\tan \delta }+\cos \beta$$$$\frac{CD}{AC}=\frac{\sin (\beta -{\theta }_1)}{\sin {\theta }_1}=\frac{\sin \beta }{\tan {\theta }_1}-\cos \beta$$$$\frac{\frac{\sin \beta }{\tan {\theta }_1}-\cos \beta }{\frac{\sin \beta }{\tan \delta }+\cos \beta }=\frac{CB}{AC}$$$$\frac{CB}{AC}=\frac{\sqrt{c^2+h^2}-\frac{l}{2}}{\frac{l}{2}}=2\sqrt{{\lambda }^2+{\xi }^2+{\eta }^2}-1$$$$\Rightarrow \frac{\frac{1}{\tan {\theta }_1}-\frac{1}{\tan \beta }}{\frac{1}{\tan \delta }+\frac{1}{\tan \beta }}=2\sqrt{{\lambda }^2+{\xi }^2+{\eta }^2}-1$$$$\frac{\mu -\frac{\eta }{\sqrt{{\lambda }^2+{\xi }^2}}}{\frac{\sqrt{{\lambda }^2-{\xi }^2}}{\mu \sqrt{{\lambda }^2+{\xi }^2}}+\frac{\eta }{\sqrt{{\lambda }^2+{\xi }^2}}}⩽2\sqrt{{\lambda }^2+{\xi }^2+{\eta }^2}-1$$$$\Rightarrow \frac{\mu \sqrt{{\lambda }^2+{\xi }^2}-\eta }{\frac{\sqrt{{\lambda }^2-{\xi }^2}}{\mu }+\eta }⩽2\sqrt{{\lambda }^2+{\xi }^2+{\eta }^2}-1$$$$$$$$example:\mu =1.5,\eta =0.3$$

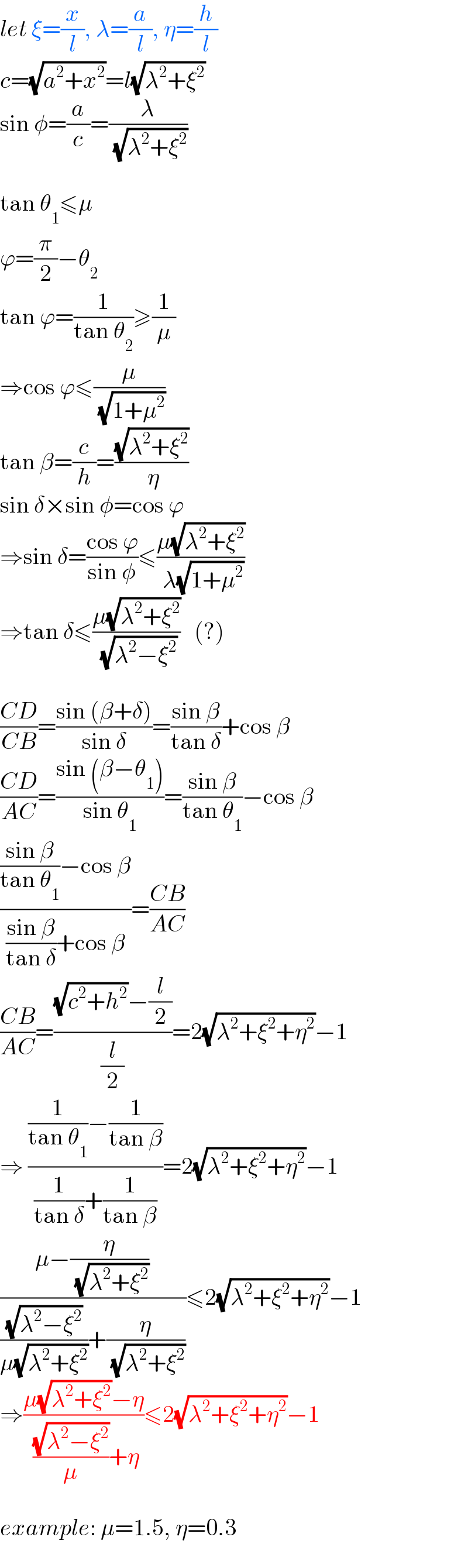
Commented by mr W last updated on 04/Oct/22

Commented by mr W last updated on 04/Oct/22

$$sincewe{don}^{\prime }thaveacontactsurface$$$$betweentherodandthestepedgein$$$$thiscase,i^{\prime }mnotsureifmysolution$$$$iscorrect.commentsarewelcome.$$

Commented by Tawa11 last updated on 04/Oct/22

$$\mathrm{Great}\mathrm{sir}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com